【数据结构】【更新中】【python】leetcode刷题记录:热题100答案 + 每日一题(附文字说明)
题目为leetcode的热题100.仅作学习用,且题目为节选,不断更新。
如果点赞过100就会制作动画
一、Hash
(1)
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target 的那 两个整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
答案:最简单的方法就是双循环,时间复杂度为N²,空间复杂度为O(1)。但时间复杂度略高。也可以用查找target - nums[i]在不在nums中来进行检索,这样操作时间会缩短一些,但无法起到质变。对于一串数字寻找关系的情况,可以想到用hash进行时间换空间的优化:
class Solution(object):
def twoSum(self, nums, target):
hashtable = dict()
for i,num in enumerate(nums):
if target-num in hashtable:
return hashtable[target - num] , i
hashtable[nums[i]] = i
return []
其中,enumerate的方法是返回索引序列,例如:
example = ['abcd','efgh']
for i,j in enumerate(example):
print(i,j)
打印结果为:
0 abcd
1 efgh
或者不要enumerate的话,也可以这么写:
class Solution(object):
def twoSum(self, nums, target):
hashtable = dict()
for i in range(len(nums)):
if target - nums[i] in hashtable:
return i, hashtable[target-nums[i]]
hashtable[nums[i]] = i
return []
注意,这里的重点一定是使用dict的结构和hash的思想相匹配。如果单纯使用list,除非提前申请(但就本题而言,需要申请相当大的list),否则会出现越界的情况。但如果使用dict结构,就可以使用键值和对应的数值来代表hash,非常方便。
双循环的方法问题在于循环导致的时间浪费,但用hash表,就可以只进行一次遍历,每次使用hash找到要遍历的元素。因此,只需要遍历一次hash即可。因此,在对一串数据进行操作时,不仅可以使用双指针,也可以使用hash表。
(2)
你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
因为需要根据各个字符串之间的联系进行分组,因此自然想到hash表,使用hash表来进行分组操作。对于原分组中的每个字符串进行讨论:原list中的字符串进行排序后赋值给t变量,若t未在hash表中,则将t作为key,将s放入key中;否则就将s添加在已经存在的key中。
因此,核心思路就是将每个字符串进行排序,并检查原字符串是否在hashtable中,并决定是将排序后的字符串作为key或是添加。
class Solution(object):
def groupAnagrams(self, strs):
hashtable = dict()
for s in strs:
t = "".join(sorted(s))
if t not in hashtable:
hashtable[t] = [s]
else:
hashtable[t].append(s)
return list(hashtable.values())
第三题不需要hash更简单,不记录了。
二、双指针
(1)移动0
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
思路:其实不需要双指针,只要得知0的个数,再删除和增添0即可。
def moveZeroes(self, nums):
n = nums.count(0)
for i in range(n):# 删一个0再加一个0
nums.remove(0)
nums.append(0)
return nums
双指针思路:设置指针a和b,指针a永远指向最前面的0,b则是不断移动的。移动规则如下:
若a内容为0,b为非0,则交换,且都向后移动;
若a为0,b为0,则b向后移动;
若a为非0,b为0,则b向后移动;
若a、b均非0,则均向后移动。
设置好初始条件后,代码如下:
class Solution(object):
def moveZeroes(self, nums):
a = b = 0
for b in range(len(nums)):
if nums[a] == 0 and nums[b] != 0:
temp = nums[a]
nums[a] = nums[b]
nums[b] = temp
a += 1
elif nums[a] != 0 and nums[b] != 0:
a += 1
return nums
(2)盛水最多的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i])
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水,返回容器可以储存的最大水量。
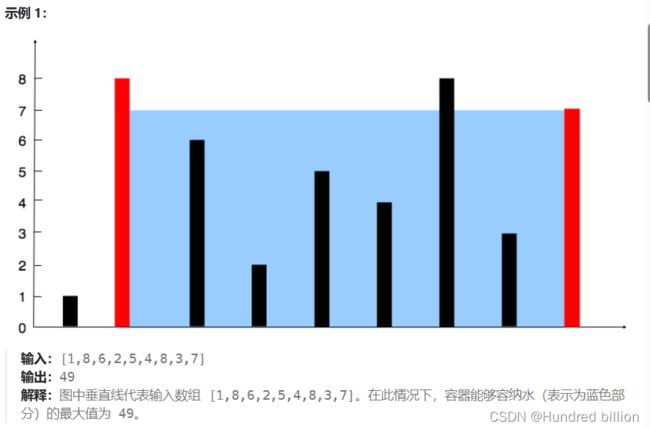
题意是选择两条柱子,以这两条柱高度的最小值为容器高度,取容器装水的量,即:
V = height[i] * (j - i)
因此暴力解法显而易见:从头开始遍历,经历两次循环得到最大值。
双指针解法如下:取指针在左右两端,假设a为左端且为短板,b为右端且为长板,那么b若向内移动,则容积一定减小,这是因为容器高取决于容器的最短边,因此b移动后,容器的高不会增大。而若向内移动a,则可能会导致体积增大,因此该算法时间复杂度为O(n):
def maxArea(self, height):
i,j,res = 0,len(height)-1,0
while i < j:
if height[i] < height[j]:
res = max(res, height[i] * (j - i))
i += 1
else:
res = max(res, height[j] * (j - i))
j -= 1
return res
(3)三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] +
nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0
- 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。
思路:先进行排序,将i固定一个元素,并以此元素向两边辐射,寻找三个元素和为0的情况。
class Solution(object):
def threeSum(self, nums):
nums.sort()
i, n = 1, len(nums)
res = []
if nums[0] > 0:
return res
while i < n-1:
left, right = (i-1), (i+1)
while left >= 0 and right <= (n-1):
t = nums[i] + nums[left] + nums[right]
if t == 0 and ([nums[left],nums[i],nums[right]] not in res):
res.append((nums[left],nums[i],nums[right]]))
elif t < 0:
right += 1
else:
left -= 1
i += 1
return res
五、数组
(1) 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大为 6 。
思路:典型的动态规划,
def maxSubArray(self, nums):
tail = len(nums) - 1
for i in range(len(nums)-1):
if nums[tail-1] + nums[tail] > nums[tail-1]:
nums[tail-1] = nums[tail-1] + nums[tail]
tail -= 1
return max(nums)
(2) 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6]. 示例 2:输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
思路:首先我们把intervals中的值全部按照区间左端点进行排序,这样可以方便我们后续的操作(对多个列表,应当有意识的把他们按某种顺序排列)。再建立一个res列表,用来存储最终结果。而算法思路也很简单,对每个元素进行扫描,如果res为空或者当前元素与res中的最后一个元素无法合并,那么就将其append进res;否则即可以合并,那就取res最后一个元素的区间右边界和当前元素的有边界的最大值作为res最后一个元素的区间右边界,即拓展区间。
有一点需要注意:为什么每次都是用res的最后一个元素比较?这是因为res是从空列表拓展出来的,且intervals数组按区间左边界排序,因此最后一个元素就是当前准备合并的元素。且不会出现漏合并的情况
例如,intervals为[[1,2],[2,2],[3,4],[2,3]],如果按照这样来执行算法,则会漏掉最后的[2,3],但由于已经排序过的原因,[2,3]的最小值2小于3,也会被排到前面,即让区间左边界越小的越往前。
代码:
class Solution(object):
def merge(self, intervals):
intervals.sort(key=lambda x: x[0])
res = []
for cur in intervals:
if not res or res[-1][1] < cur[0]:
res.append(cur)
else: #存在重叠
res[-1][1] = max(res[-1][1],cur[1])
return res
写法上,是遍历intervals中的每个元素。如果用双指针的方式遍历会导致耗费时间较高,但也给出代码:
class Solution(object):
def merge(self, intervals):
i, n= 0, len(intervals)
intervals.sort(key=lambda x: x[0])
while i < n:
cur = intervals[i]
j = i+1
while j < n:
temp = intervals[j]
if temp[0] <= cur[1] or temp[1] <= cur[1]:
cur[1] = max(cur[1],temp[1])
intervals.pop(j)
j -= 1
n -= 1
j += 1
i += 1
return intervals
(3) 轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步:
[7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: [5,6,7,1,2,3,4]
思路:最简单的就是进行python切片,先对k进行模除。然后将后k位和前面的数字交换:
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
k = k % len(nums)
res = nums[-k:]+nums[0:-k]
for i in range(len(nums)):
nums[i] = res[i]
但这样需要新开一个数组,导致空间复杂度为O(n),下面是原地排序的方法:先将全部数逆转,再将前k位逆转,后面的(n-k)位逆转即可。
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
k, n= k % len(nums), len(nums)
nums.reverse()
nums[:k] = nums[(k-n)-1:-n-1:-1]
nums[k:] = nums[:(k-n)-1:-1]
(4) 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
思路:使用左右数组,最后左右数组对应项相乘即可得到答案。
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
n= len(nums)
L, R, res = [1]*n, [1]*n, [0]*n
for i in range(1,n):
L[i] = nums[i-1] * L[i-1]
R[-i-1] = nums[-i] * R[-i]
for i in range(n):
res[i] = L[i] * R[i]
return res
二叉树
二叉树的基本遍历方式可以看,本节的题有使用下文的算法:
【数据结构】【树的遍历算法】【python】树的各种遍历算法
(1)二叉树对称
给你一个二叉树的根节点 root , 检查它是否轴对称。
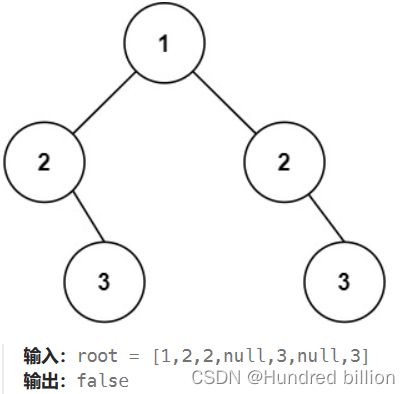
思路:可以有多种做法。比如利用左右根和右左根的遍历来检查是否对称,不过那样的代码效率比较差。也可以用下面的方法,如果左子树的左节点和右子树的右节点存在,左子树的右节点和右子树的左节点存在,且值相同就可以判断为对称的。反之则是不对称的。具体代码细节在注释:
class Solution(object):
def isSymmetric(self, root):
def check(left,right):
# 两方都不存在 true
if not left and not right:
return True
# 如果有一方不存在则为flase
elif not left or not right:
return False
#两方都存在
if left.val != right.val:
return False
return check(left.left,right.right) and check(left.right,right.left)
return check(root,root)
(2)二叉树的直径
给你一棵二叉树的根节点,返回该树的直径 。
二叉树的直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
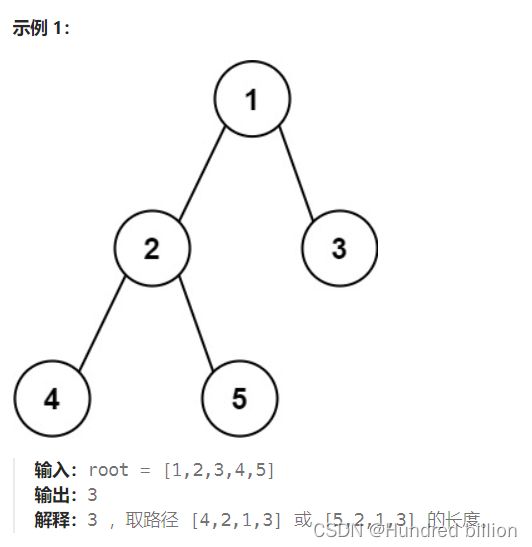
这题的思路即DFS.使用深度优先遍历的思想,记录每个节点的深度,进而与res比较,若遇到左子树深度加右子树深度大于当前记录的最大值时,就进行替换。最后返回的值就是res。代码:
class Solution(object):
def diameterOfBinaryTree(self, root):
self.res = 0
def DFS(root):
if not root:
return 0
left = DFS(root.left)
right = DFS(root.right)
if self.res < left + right:
self.res = left + right
return max(left,right)+1
DFS(root)
return self.res
实际上,本题只是DFS的一个变体,用res记录L+R的最大值。
(3) 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
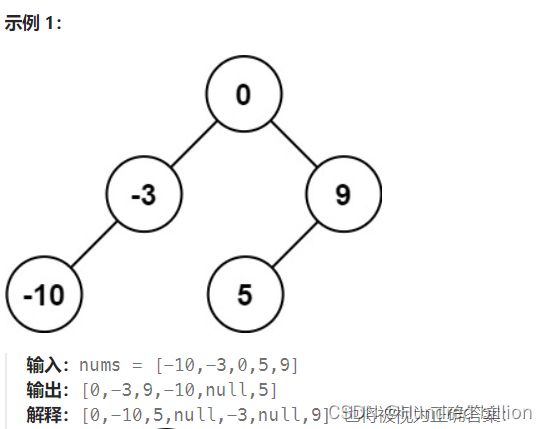
思路:当存储方式是数组的时候,解决这个问题就会比较简单。本题没有规定要构造成什么样的平衡二叉树,而只是一颗平衡二叉树,因此,选择好根节点,再将原数组一分为二即可,很有二分查找的感觉。但本题是构造一棵树,返回的结果是TreeNode类型,因此使用递归更加简单。代码如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def sortedArrayToBST(self, nums):
def midorder(L,R):
if L > R:# 边界条件
return None
mid = (L + R) // 2
#思路类似于二分查找
root = TreeNode(nums[mid])
root.left = midorder(L,mid-1)
root.right = midorder(mid+1,R)
return root
return midorder(0,len(nums)-1)
二分法
本章的内容都基于二分查找的思想。
给你一个满足下述两条属性的 m x n 整数矩阵:每行中的整数从左到右按非严格递增顺序排列。每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
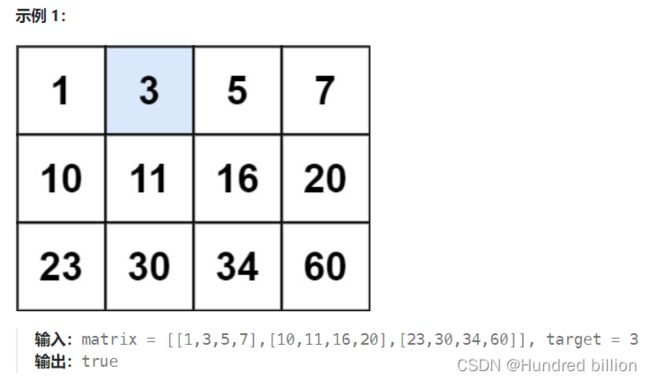
思路一:因为是有序的排列,因此如果想做出本题非常容易:对矩阵的每一行进行遍历,如果遇到元素值大于target时,则直接返回false,因为整体有序,不可能再出现相等的值。时间复杂度则是O(n)
class Solution(object):
def searchMatrix(self, matrix, target):
for i in range(len(matrix)):
for j in range(len(matrix[i])):
t = matrix[i][j]
if t == target:
return True
elif t > target:
return False
# 最后的false是满足查找不到的情况,即target大于矩阵中最大值的情况。
return False
思路二:二分查找:
和普通的二分查找不同的是,这是一个矩阵,因此二分查找的方式不能直接进行查找,需要进行一定的转换。
思想还是二分查找的思想,将整个矩阵看成一个数组,left = 0,right为最后一个元素。mid仍取中间值。重点是x,y如何确定,确定x,y后就可以与target进行比较并确定mid的位置。x是用mid // col,即除一行的元素个数,例如mid = 5,col = 4,则x = 1,确定为第一行。列元素则是取模运算,例如mid = 7,col = 4,则y = 3。在涉及行列转换的时候,可以多考虑取模或整除运算。
class Solution(object):
def searchMatrix(self, matrix, target):
row,col = len(matrix),len(matrix[0])
left, right = 0, row*col -1
while left <= right:
mid = (left + right) // 2
x, y = mid // col , mid % col
if matrix[x][y] == target:
return True
elif matrix[x][y] > target:
right = mid - 1
else:
left = mid + 1
return False
(2)在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4] 示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1] 示例 3:
输入:nums = [], target = 0 输出:[-1,-1]
思路:如果仅以通过来说,先找到第一个target的下标,再依次向后找依然可以通过本题,但不满足时间复杂度为O(logn)。实际上,本题的logn和非递减序列也说明了需要使用二分查找。对于本题,进行两次二分查找即可,第一次找到第一个,第二次找到最后一个。与普通二分查找不同的是,找第一个或者第二个的二分查找需要在当前值等于target时仍要改变指针的方向,因为我们要找的是target序列的第一个或者最后一个。具体细节见代码:
class Solution(object):
def searchRange(self, nums, target):
#这样赋初值可以解决空列表的情况
res = [-1,-1]
left, right= 0,len(nums)-1
# 找第一个
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
res[0] = mid
#因为是找第一个,即要找当前指向元素或其左边的元素
right = mid - 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] < target:
left = mid + 1
left,right= 0,len(nums)-1
# 找最后一个
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
res[1] = mid
#因为是找最后一个,即要找当前指向元素或其右边的元素
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] < target:
left = mid + 1
return res
栈
(1)有效括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
1.左括号必须用相同类型的右括号闭合。
2.左括号必须以正确的顺序闭合。
3.每个右括号都有一个对应的相同类型的左括号。

思路:本题只是利用栈的特性,较为简单,可以使用字典进行匹配的判断。
将左括号入栈,当遇到右括号时,将栈顶元素pop出来,并和当前的右括号尝试配对,如果无法配对则返回fasle。若可以配对则继续遍历。若出现了栈为空但此时遍历到右括号,则一定无法配对,也是false。
最后返回时判断栈是否为空,若为空则完成配对,否则是左括号多于右括号,返回False。
lass Solution(object):
def isValid(self, s):
stack = []
dic = {'{': '}', '[': ']', '(': ')'}
for string in s:
if string in dic:
stack.append(string)
elif len(stack) == 0:# 提前栈空 无法配对
return False
elif dic[stack.pop()] != string:
return False
return len(stack) == 0
(2)最小栈

思路:如果仅仅是做出本题,那会非常简单。仅仅是多封装了一个函数而已:
class MinStack(object):
def __init__(self):
self.stack = []
def push(self, val):
self.stack.append(val)
def pop(self):
self.stack.pop()
def top(self):
return self.stack[-1]
def getMin(self):
return min(self.stack)
但如果在常数时间内返回,那显然就不能使用min函数,也就需要在push、pop中进行额外操作。我们设计一个最小栈的结构,来记录每次push操作之后stack中的最小值,因此getMin的操作就可以在O(1)中返回最小值。
class MinStack(object):
def __init__(self):
self.stack = []
# 最小栈存储每次push后的最小值,栈顶的当前栈的最小栈
self.min_stack = [float('inf')]
def push(self, val):
self.stack.append(val)
# 如果当前值val没有最小栈的栈顶值s小,则再记录一次最小值s
# 这样在pop的时候,stack中的val被pop出去,不影响最小栈的最小值仍为s
self.min_stack.append(min(val,self.min_stack[-1]))
def pop(self):
self.stack.pop()
self.min_stack.pop()
def top(self):
return self.stack[-1]
def getMin(self):
return self.min_stack[-1]
每日一题:
(1)
给你一个下标从 0 开始的数组 nums ,数组长度为 n 。
nums 的 不同元素数目差 数组可以用一个长度为 n 的数组 diff 表示,其中 diff[i] 等于前缀 nums[0, …, i] 中不同元素的数目 减去 后缀 nums[i + 1, …, n - 1] 中不同元素的数目。
返回 nums 的 不同元素数目差 数组。
注意 nums[i, …, j] 表示 nums 的一个从下标 i 开始到下标 j 结束的子数组(包含下标 i 和 j 对应元素)。特别需要说明的是,如果 i > j ,则 nums[i, …, j] 表示一个空子数组。

思路:看起来还怪麻烦的,实际写起来也不是很容易…
前文说过,当遇到一串数字找其中规律,或者根据数字之间的关系来解决问题,可以考虑hash的想法,因此可以使用hash的思想来解决问题。同时,本题的关键是前后部分中不同的字符数,因此需要想到集合这个数据元素,因为其天然具有划分重复数据元素的特性。如果没想到集合将会浪费额外精力去处理重复数据的个数。本题的核心思想也就是两个集合的长度做差
首先先用cnt这个列表来记录后缀中重复的个数,为什么是后缀呢?第二个for循环是从0到n的遍历,即获得前缀的集合长度,因此先获取后缀重复的个数,对之后的操作更简单。记录得到后缀的重复个数后,通过第二个for循环得到diff的值。
class Solution(object):
def distinctDifferenceArray(self, nums):
st, n = set(), len(nums)
diff, cnt = [], [0]*(n+1)
for i in range(n - 1,0,-1):
st.add(nums[i])
cnt[i] = len(st)
st.clear()
for i in range(n):
st.add(nums[i])
diff.append(len(st) - cnt[i + 1])
return diff
class Solution {
public:
vector<int> distinctDifferenceArray(vector<int>& nums) {
int n = nums.size();
unordered_set<int> st;
vector<int> sufCnt(n + 1, 0);
for (int i = n - 1; i > 0; i--) {
st.insert(nums[i]);
sufCnt[i] = st.size();
}
vector<int> res;
st.clear();
for (int i = 0; i < n; i++) {
st.insert(nums[i]);
res.push_back(int(st.size()) - sufCnt[i + 1]);
}
return res;
}
};
(2)1690 石子游戏
石子游戏中,爱丽丝和鲍勃轮流进行自己的回合,爱丽丝先开始 。
有 n 块石子排成一排。每个玩家的回合中,可以从行中 移除 最左边的石头或最右边的石头,并获得与该行中剩余石头值之 和 相等的得分。当没有石头可移除时,得分较高者获胜。
鲍勃发现他总是输掉游戏(可怜的鲍勃,他总是输),所以他决定尽力 减小得分的差值 。爱丽丝的目标是最大限度地 扩大得分的差值 。
给你一个整数数组 stones ,其中 stones[i] 表示 从左边开始 的第 i 个石头的值,如果爱丽丝和鲍勃都 发挥出最佳水平 ,请返回他们 得分的差值 。

思路:对于这种逐渐更改数组,并且在更改过程中需要记录数据,设计策略,那么就很可能是动态规划/带备忘录搜索(记忆化搜索)。而动态规划的重点就是从小规模问题拓展到大规模,从小规模的问题入手解决大规模问题。因此首要问题就是找到核心的小规模问题。
Alice的目的是让她的分数(A)减去Bob的分数的值最大,A-B最大,而Bob则要尽力缩小这个差距,反过来说,也就是B-A最大。而所谓的Alice先手,实际上也会在Alice完成一次操作后,变成Bob先手,这点也满足动态规划的要求。
也就是说,对于上图的实例:
移除最左边的石子 stones[0]=5,剩余石子为 stones′=[3,1,4,2]
问题变成了鲍勃(他现在是先手)的得分减去爱丽丝(她现在是后手)的得分最大是多少。
移除最右边的石子 stones[4]=2,剩余石子为stones′=[5,3,1,4]
问题变成了鲍勃(他现在是先手)的得分减去爱丽丝(她现在是后手)的得分最大是多少。
因此,如果先拿走左边的石头,那么Alice的得分就是右边石头数值的和(S1),得分差就是S1-dfs(i+1,j);
如果先拿走右边的石头,那么那么Alice的得分就是左边石头数值的和(S2),得分差就是S2-dfs(i,j-1).
而S1或者S2的和的求法,可以使用前缀和的差值计算。如果每次都要求一次中间若干数值的和,那将会耗费额外的时间。因此现在代码的起始位置计算好stones数组的前缀和,而计算S1/S2时直接做差即可。
记忆化搜索代码如下。但似乎在leetcode无法通过,因为无法import第三方库,因此cache的装饰器无法使用。如果去掉装饰器的部分,会导致有用例超时。如果在本地运行可以正确执行。
from functools import cache
class Solution(object):
def stoneGameVII(self, stones):
pre, n = [0], len(stones)
#pre 是前缀和
for i in stones:
pre.append(pre[-1] + i)
@cache
def dfs(i,j):
#不存在
if i > j:
return 0
return max(pre[j+1] - pre[i+1] - dfs(i+1,j), pre[j] - pre[i] - dfs(i,j-1))
res = dfs(0,n-1)
dfs.cache_clear()
return res
思路二:动态规划
如果将思路一的过程改为动态规划,即自底向上的进行构造,就可以不使用递归的方式,因此也就不需要使用装饰器,因此时间复杂度也可以得到缓解。我们可以首先求出区间 [i,i] 的最大得分差值,然后不断向外扩展求出 [i−1,i],[i,i+1] 区间的最优解,一直扩展到区间 [0,n−1],此时即可求出最优解返回即可。
class Solution(object):
def stoneGameVII(self, stones):
n = len(stones)
sum_arr = [0] * (n + 1)
dp = [[0] * n for _ in range(n)]
for i in range(n):
sum_arr[i + 1] = sum_arr[i] + stones[i]
for i in range(n - 2, -1, -1):
for j in range(i + 1, n):
dp[i][j] = max(sum_arr[j + 1] - sum_arr[i + 1] - dp[i + 1][j], sum_arr[j] - sum_arr[i] - dp[i][j - 1])
return dp[0][n - 1]