Xilinx Vivado复数乘法器Complex Multiplier IP核调用及其仿真
Complex Multiplier IP核的使用，尤其是输出数据的截位到底怎么弄，我感觉官方文档PG104写的不清楚。我个人在网上也没找到好的讲解文章，就自己琢磨了下，然后写成文档记录在此，方便将来也有疑问的同学。
目录
一、如下是我的仿真代码：
二、testbench中的IP设置如下：
三、几个关键点的理解如下：
1、当IP输出位宽为默认的最大值25时，此时IP没有截位。如仿真例子中第一种方法：
2、当IP输出位宽设置为20时，此时IP相对于最大值25就截掉了5位。如仿真例子中第二种方法：
3、如上第2点使用同一个IP设置：IP输出位宽设置为20时，此时IP相对于最大值25就截掉了5位。但修改输入数据的使用方法，如仿真例子中第三种方法：
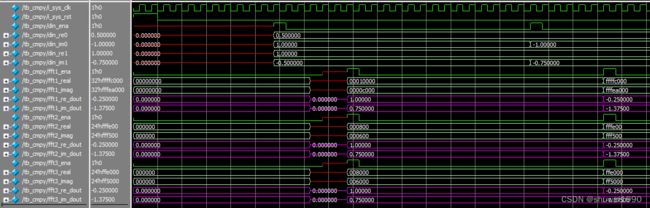
4、modelsim仿真结果如下所示，可以看到仿真结果是正确的。
一、如下是我的仿真代码：
/*-------------------------------------------------------------------------------------------------------------------
Author: Zheng Wei
Date: 2022-10-10
Version: 1.0
Description: It is a tb_cmpy test.
-------------------------------------------------------------------------------------------------------------------*/
`timescale 1ns / 1ps
module tb_cmpy;
reg i_sys_clk ;
reg i_sys_rst ;
reg din_ena ;
reg [9 :0] din_re0 ;
reg [9 :0] din_im0 ;
reg [9 :0] din_re1 ;
reg [9 :0] din_im1 ;
// clock generate module
parameter period = 10; // 100MHz
initial begin
i_sys_clk = 1'b0;
forever #(period/2) i_sys_clk = ~i_sys_clk;
end
//-------------------------------------------------------------------
// system initialization
task task_sysinit;
begin
end
endtask
// system reset
task task_reset;
begin
i_sys_rst = 1'b1;
repeat(2) @(negedge i_sys_clk);
i_sys_rst = 1'b0;
end
endtask
initial begin
task_sysinit;
task_reset ;
repeat(10) @(posedge i_sys_clk);
// 10bit: 1 sign bit, 1 integer bit, 8 fraction bit
// case1: x0 = 0.5 + j; x1 = 1 - 0.5j
// result: x0 * x1 = 1 + 0.75j, 1 sign bit, 1 integer bit, 8 fraction bit
din_ena = 1;
din_re0 = 10'b00_1000_0000;
din_im0 = 10'b01_0000_0000;
din_re1 = 10'b01_0000_0000;
din_im1 = 10'b11_1000_0000;
@(posedge i_sys_clk);
din_ena = 0;
repeat(20) @(posedge i_sys_clk);
// 10bit: 1 sign bit, 1 integer bit, 8 fraction bit
// case2: x0 = 0.5 - j; x1 = 1 - 0.75j
// result: x0 * x1 = -0.25 - 1.375j, 1 sign bit, 1 integer bit, 8 fraction bit
din_ena = 1;
din_re0 = 10'b00_1000_0000;
din_im0 = 10'b11_0000_0000;
din_re1 = 10'b01_0000_0000;
din_im1 = 10'b11_0100_0000;
@(posedge i_sys_clk);
din_ena = 0;
repeat(500) @(posedge i_sys_clk);
$stop;
end
//------------ first method ---------------------------------------------------------------
wire fft1_ena ;
wire signed [31:0] fft1_real ;
wire signed [31:0] fft1_imag ;
wire signed [11:0] fft1_re_dout;
wire signed [11:0] fft1_im_dout;
// din: real[11:0], image[27:16]; dout: real[24:0], image[56:32].
cmpy_1 u1_cmpy(
.aclk (i_sys_clk ), // input wire aclk
.s_axis_a_tvalid (din_ena ), // input wire s_axis_a_tvalid
.s_axis_a_tdata ({4'd0,{2{din_im0[9]}},din_im0,4'd0,{2{din_re0[9]}},din_re0}), // input wire [31 : 0] s_axis_a_tdata
.s_axis_b_tvalid ( 1'b1 ), // input wire s_axis_b_tvalid
.s_axis_b_tdata ({4'd0,{2{din_im1[9]}},din_im1,4'd0,{2{din_re1[9]}},din_re1}), // input wire [31 : 0] s_axis_b_tdata
.m_axis_dout_tvalid (fft1_ena ), // output wire m_axis_dout_tvalid
.m_axis_dout_tdata ({fft1_imag,fft1_real} ) // output wire [63 : 0] m_axis_dout_tdata
);
assign fft1_re_dout = fft1_real[8+:12]; // [19:8]: shift right 8 bit
assign fft1_im_dout = fft1_imag[8+:12]; // [19:8]: shift right 8 bit
//------------ second method ---------------------------------------------------------------
wire fft2_ena ;
wire signed [23:0] fft2_real ;
wire signed [23:0] fft2_imag ;
wire signed [11:0] fft2_re_dout;
wire signed [11:0] fft2_im_dout;
// din: real[11:0], image[27:16]; dout: real[19:0], image[43:24].
cmpy_0 u2_cmpy(
.aclk (i_sys_clk ), // input wire aclk
.s_axis_a_tvalid (din_ena ), // input wire s_axis_a_tvalid
.s_axis_a_tdata ({4'd0,{2{din_im0[9]}},din_im0,4'd0,{2{din_re0[9]}},din_re0}), // input wire [31 : 0] s_axis_a_tdata
.s_axis_b_tvalid ( 1'b1 ), // input wire s_axis_b_tvalid
.s_axis_b_tdata ({4'd0,{2{din_im1[9]}},din_im1,4'd0,{2{din_re1[9]}},din_re1}), // input wire [31 : 0] s_axis_b_tdata
.m_axis_dout_tvalid (fft2_ena ), // output wire m_axis_dout_tvalid
.m_axis_dout_tdata ({fft2_imag,fft2_real} ) // output wire [47 : 0] m_axis_dout_tdata
);
assign fft2_re_dout = fft2_real[3+:12]; // [14:3]: shift right 8-5=3 bit
assign fft2_im_dout = fft2_imag[3+:12]; // [14:3]: shift right 8-5=3 bit
//------------ third method ---------------------------------------------------------------
wire fft3_ena ;
wire signed [23:0] fft3_real ;
wire signed [23:0] fft3_imag ;
wire signed [11:0] fft3_re_dout;
wire signed [11:0] fft3_im_dout;
// din: real[11:0], image[27:16]; dout: real[19:0], image[43:24].
cmpy_0 u3_cmpy(
.aclk (i_sys_clk ), // input wire aclk
.s_axis_a_tvalid (din_ena ), // input wire s_axis_a_tvalid
.s_axis_a_tdata ({4'd0,din_im0,2'd0,4'd0,din_re0,2'd0}), // input wire [31 : 0] s_axis_a_tdata
.s_axis_b_tvalid ( 1'b1 ), // input wire s_axis_b_tvalid
.s_axis_b_tdata ({4'd0,din_im1,2'd0,4'd0,din_re1,2'd0}), // input wire [31 : 0] s_axis_b_tdata
.m_axis_dout_tvalid (fft3_ena ), // output wire m_axis_dout_tvalid
.m_axis_dout_tdata ({fft3_imag,fft3_real} ) // output wire [47 : 0] m_axis_dout_tdata
);
assign fft3_re_dout = fft3_real[7+:12]; // [18:7]: shift right 8+4-5=7 bit
assign fft3_im_dout = fft3_imag[7+:12]; // [18:7]: shift right 8+4-5=7 bit
endmodule二、testbench中的IP设置如下：
- IP cmpy_1的设置如下：两个输入都设置成12bit，输出默认的25bit；
- IP cmpy_0的设置如下：两个输入都设置成12bit，但输出设置为20bit；
三、几个关键点的理解如下：
1、当IP输出位宽为默认的最大值25时，此时IP没有截位。如仿真例子中第一种方法：
两个输入数据都是10bit宽，其中8bit为定点小数，实际上就是都左移8bit；那么相乘的结果就是左移了16bit，如果相乘的结果也是取8位为定点小数（即实际上右移8bit），那么就还需要右移8bit才能得到正确的值，也即如下代码：
assign fft1_re_dout = fft1_real[8+:12]; // [19:8]: shift right 8 bit2、当IP输出位宽设置为20时，此时IP相对于最大值25就截掉了5位。如仿真例子中第二种方法：
两个输入数据都是10bit宽，其中8bit为定点小数，实际上就是都左移8bit；那么相乘的结果就是左移了16bit，如果相乘的结果也是取8位为定点小数（即实际上右移8bit），那么就还需要右移8bit才能得到正确的值。但是因为IP已经帮我们截掉了5bit，所以此时我们只需要再截掉8-5=3bit就行了，也即如下代码：
assign fft2_re_dout = fft2_real[3+:12]; // [14:3]: shift right 8-5=3 bit3、如上第2点使用同一个IP设置：IP输出位宽设置为20时，此时IP相对于最大值25就截掉了5位。但修改输入数据的使用方法，如仿真例子中第三种方法：
仿真中给的两个输入数据都是10bit，但IP设置的输入数据位宽是12bit，那么就需要将10bit拓宽到12bit。有两种办法：
- 如前面两个仿真例子，都是直接复制符号位进行拓宽到指定长度；
- 如第三个仿真例子，是直接在结尾补0进行拓宽到指定长度。
现在来仔细讲下结尾补0的方法如何进行截位。本来两个都是10bit的数据，其中8bit为定点小数，实际上就是都左移8bit；但现在结尾补了2bit的0，那也就是总共左移了8+2=10bit了。
那么相乘的结果就是左移了20bit，如果相乘的结果也是取8位为定点小数（即实际上右移8bit），那么就还需要右移12bit才能得到正确的值。但是因为IP已经帮我们截掉了5bit，所以此时我们只需要再截掉12-5=7bit就行了，也即如下代码：
assign fft3_re_dout = fft3_real[7+:12]; // [18:7]: shift right 8+4-5=7 bit4、modelsim仿真结果如下所示，可以看到仿真结果是正确的。
本文完结！