面经问题收录

主要的内容来自于准备考研复试时的问题，想着这些问题以后找工作面试也可能被问到，随时记录，随时更新

面经地址：
https://cloud.tencent.com/developer/article/1415560

计算机网络

物理层

数据链路层

网络层

传输层

描述一下TCP三次握手

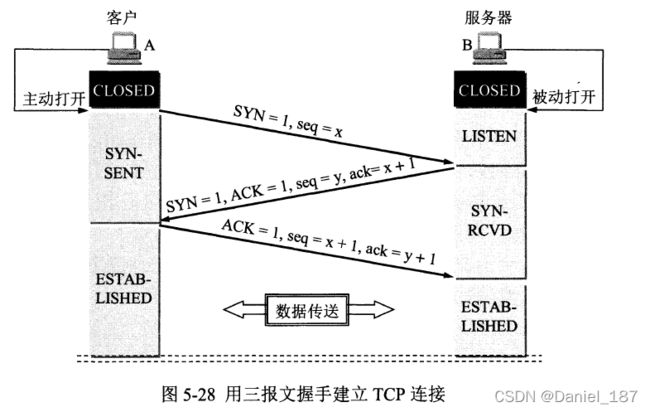
首先TCP三次握手是用来建立TCP连接的一个过程，这个过程需要发送3个数据包，故称为3次握手
以客户端发起请求为例：首先客户端发送连接请求数据包，SYN=1，并选定一个seq=x，然后客户端进入SYC-SENT状态。服务器收到该数据包后，对其进行确认，SYN=1，ACK=1，并选定一个seq=y，同时置ack=x+1，然后服务器从LISTEN状态进入SYN-RECVD状态。最后客户端对服务器发来的数据包进行确认，ACK=1，seq=x+1，ack=y+1，然后客户端进入ESTABLISHED状态，服务器收到该确认后，也进入ESTABLISHED状态。至此，三次握手完成，TCP连接建立成功

tcp三次握手，最后一个ack丢失会怎样，这时候发送方发送数据会怎样

服务器端：超时重传

客户端：在linux c 中，client 一般是通过 connect() 函数来连接服务器的，而connect()是在 TCP的三次握手的第二次握手完成后就成功返回值。也就是说 client 在接收到 SYN+ACK包，它的TCP连接状态就为 established （已连接），表示该连接已经建立。那么如果 第三次握手中的ACK包丢失的情况下，Client 向 server端发送数据，Server端将以 RST包响应，方能感知到Server的错误

三次握手中的第二个数据包也可以分开传送，即服务端先发送ACK对第一个数据包进行确认，然后再发送SYN同步报文段，这样，三次握手就变成了四次握手，但效果是一样的

描述一下TCP四次挥手

TCP四次挥手是用来释放TCP连接的一个过程，这个过程需要发送4个数据包，故称为4次挥手

以客户端主动释放连接为例：首先客户端发送FIN=1的数据包，然后进入FIN-WAIT1状态。服务器收到后，发送ACK=1的数据包进行确认。服务器进入CLOSE-WAIT状态，客户端收到后进入FIN-WAIT2状态，此时连接半关闭，数据只能单向地从服务器发往客户端。如果服务器没有数据发送，则发送FIN=1的数据包，请求关闭连接，并进入LAST-ACK状态。客户端收到后，发送ACK=1对其进行确认，并进入TIME-WAIT状态。服务端收到该确认后，进入CLOSE状态，连接被关闭。客户端经过2MSL的时间后，进入CLOSE状态，连接被关闭。

为什么客户端要等待2MSL时长

防止最后一个确认报文丢失，导致服务器无法正常进入关闭状态。

如果最后的确认报文丢失了，则服务器会超时重传第三个FIN报文，则客户端在该时间内就能对其进行确认。否则服务器无法正常进入关闭状态。

时长之所以是2MSL，主要是考虑到一种极端情况：假设最后的确认报文就是在MSL时丢失的，而服务器的重传报文到达客户端又经过了MSL的时间，这是最糟的一种情况，但是客户端能够对其进行响应。

TCP四次挥手，为什么不是三次？

TCP为全双工通信，每个方向都需要一个FIN和ACK，共有4个数据包，故称为4次挥手。

客户端到服务器的连接经过前两次握手已经被关闭。此后，服务器可能有数据向客户端传送，传送完成后服务器发送FIN关闭连接，客户端发送ACK予以确认。

可见，如果服务器收到FIN后直接发送ACK+FIN，也就是中间没有数据传送，则四次挥手就可以简化为三次挥手

time_wait作用？

1. 保证客户端发送的最后一个ACK数据包能够正确到达服务器：如果该数据包丢失，则经过MSL后服务器重传FIN，其最晚会经过MSL后到达客户端，因此需要等待2MSL的时间
2. 防止“已经失效的连接请求报文段”出现在本连接中。经过2MSL时长可以使本次连接产生的所有报文段都从网络中消失，可以保证下一个新的连接中不会出现旧的连接请求报文段

TCP和UDP的区别

1. TCP是面向连接的，可靠的传输协议，它的传输单位是字节流
2. UDP是一个非连接的协议，它尽最大努力交付，并不保证可靠交付，它的传输单位是数据包

TCP能改成两次握手三次挥手吗？

不能改成两次握手：设想这样一种情况，如果客户端的第一个握手数据包在网络某个节点滞留很长时间，导致客户端超时重新握手，第二次握手建立成功，并完成数据通信后，断开连接。如果第一个握手数据包在断开连接后到达了服务器，则服务器认为又有一个新的连接，然后它发送ack进行确认，但是客户端并不会理会，因为它没有发起连接。如果是两次握手的话，则服务器发送完那个ack后就认为连接建立成功，等待客户端发来数据，但是这种等待显然是没意义的。所以我们需要第三个握手数据包，再对连接进行确认

能改成三次挥手：改成三次挥手就不能再有半关闭状态，也就是将第二个和第三个数据包合二为一，中间没有服务器向客户端单向发送数据这个过程

TCP报文段最长多少字节

IP数据报的最大长度-IP数据报的首部-TCP报文段的首部=65535-20-20=65495

应用层

操作系统

描述系统调用的过程

系统调用号送eax
参数送寄存器
int 0x80

内核根据系统调用号转入响应的服务例程
从TSS中读出SS和SP，切换到内核栈，将用户态的断点和程序状态保存到内核栈中

进程管理

linux打开一个可执行文件的流程

shell首先fork一个子进程
然后执行exec，使用子进程的进程映像替换掉当前的进程
将pc设置为子进程的第一条指令开始执行，但是此时os还没有把代码调入内存，所以会产生缺页中断，然后os负责将代码调入内存

哲学家进餐问题如何避免死锁：

1. 保证每个哲学家拿叉子互斥，即对哲学家拿起左右两只叉子这个过程上锁保护
2. 令奇数号哲学家先拿左手边的叉子，偶数号的哲学家先拿右手边的叉子
3. 至多允许4名哲学家同时吃饭

什么是安全状态？介绍银行家算法

  安全状态：
  在某一时刻，系统能够按照某种进程顺序为每个进程分配其所需的资源，直至最大需求，使每个进程均可顺利完成，则称此时系统的状态为安全状态，称这样的一个进程序列为安全序列
  
  银行家算法：
  银行家算法涉及以下几个数据结构：一个可用资源向量available，记录系统中各类资源的当前可利用数目；最大需求矩阵max，记录每个进程对各类资源的最大需求量；分配矩阵allocation，记录每个进程对各类资源的当前占有量；需求矩阵need，记录每个进程对各类资源尚需要的数目，need=max-allocation；请求向量request。
  每当操作系统接收到一个请求向量，它首先检查request是否大于need，若大于则出错，然后检查其是否大于available，若大于，则说明系统中没有足够的资源，将该进程阻塞。
  接着系统试着将资源分配给进程，available-request，并执行安全性检查算法：尝试寻找系统中是否有安全序列，若有则将资源分配给进程，否则将进程阻塞

内存管理

描述虚实地址转换的过程

以32位虚拟地址向物理地址的转换为例，高20位为虚页号，低12位为页内地址，虚页号的高10位指向页目录表中的一个页目录项，该页目录项指向一个页表，然后用虚页号的低10位找到页表中页表项，得到物理页号，将该物理页号拼接上12位的页内地址就得到了物理地址。
如果有TLB的话，进行上面的过程的同时还会查询TLB(Translation Lookaside Buffer)，此时将虚页号分为组索引和标记两部分，根据组索引定位到组，然后比对标记和有效位观察是否命中，如果命中，则终止内存中的慢表查询，直接得到了物理页号，进而得到物理地址。否则继续访问慢表，并更新TLB   
得到物理地址后，会查询cache，假设采用组相连的映射方式，地址被分为标记，组号和块内地址三部分，首先定位到组，然后比对是否有满足要求的tag，若存在，则从数据块中偏移块内地址的位置取出数据送到CPU，并终止内存的访问。否则cache未命中，继续访问内存，并将更新cache

数据结构

线性表

链表带有头节点有什么好处

对空表和非空表的处理更加统一，比如当我们插入一个新节点时无需判断表是否为空，直接将新节点挂接在头节点后面即可
对于删除操作也是同理，如果我们把最后一个节点free了，对于不带头节点的链表还需要将链表指针置为null

怎么判断单链表有环

使用快慢指针，快指针每次走两个节点，慢指针每次走一个节点。可以证明，如果链表中存在环，则快指针一定会从后面追上慢指针，所以如果判断快慢指针指向了相同节点，就说明链表中有环；反之如果快指针走到了链表的尾节点，即next=NULL，说明链表中没有环

栈和队列

如何区分队空和队满

对于数组实现的循环队列，可以牺牲一个存储空间来区分队空和队满：队空时front和rear指向同一个空间，队满时(rear+1)%MAXSIZE==front
或者也可以设置一个变量记录队列的size，size=0时队空

树

树的存储结构有哪些？

1. 使用数组按节点顺序存储，但是这只适用于树比较满的情况，否则会造成空间浪费
2. 使用二叉链表存储，采用长子兄弟表示法，左指针指向该节点的第一个子节点，右指针指向该节点的右兄弟
3. 采用结构数组的方式，每个节点保存其父节点在数组中的下标，指向父节点，根节点的父节点设置为-1

图

图的遍历

图的遍历的时间复杂度是多少？

对于DFS和BFS，采用邻接矩阵时间复杂度是O(V^2)，采用邻接表时间复杂度是O(V+E)

用DFS和BFS分别遍历一个完全图，得到的生成树树高分别为多少？

用DFS遍历完全图，得到的生成树树高是顶点总数；用BFS遍历完全图，得到的生成树树高是2

DFS和BFS的应用场景

BFS：树的层序遍历；无权图的单源最短路问题；处理多个状态的问题，比如数组里面的跳跃，八数码问题
DFS：树的前序中序后序遍历属于DFS

最小生成树

最小生成树的定义

图的所有生成树中边的权值最小的那棵树
生成树：包含图G中所有顶点的一个极小连通子图

Prim算法原理

prim算法过程可以概括为从一个顶点出发让一棵小树长大的过程：
我们用T={V，E}来描述一棵树的话，首先选定一个起始点S将其加入V，然后选择与它相邻的权值最小的边将其加入E，并将其邻接点A加入V。然后考虑对于新加入的邻接点A，其他顶点是否会因为A的加入而变得离当前树的距离更紧，如果是则更新这个距离。
然后重复次过程，每次选择一个权值最小的边，将该边和顶点加入T集合中
时间复杂度：O(V^2)

Kruskal算法原理

它是按照网图中边的权值递增的顺序构造最小生成树的算法，过程可以概括为将n个孤立的顶点森林逐步合并为一棵生成树的过程
每次选择剩下的边集中权值最小的边，如果该边的两个顶点不在当前森林的同一棵树上，就将其加入最小生成树，这个判定过程可以使用并查集来实现。
时间复杂度：
建堆：O(E)
调整为堆：O(logE)
总的时间复杂度：O(E*logE)

最短路径

Dijkstra算法

类似于Prim算法求最小生成树：我们需要设置D和P这两个数组，D用于记录源点到当前节点的最短距离，P用于记录在最短路径上当前节点的父节点。
最开始将源点加入最短路径，然后寻找距离它最近的顶点加入最短路径，并用P数据记录它的前驱节点。然后更新D数组，观察是否因为新节点的加入而导致其他顶点到当前的最短路径的距离变得更小，如果变得更小，则更新D中的值，然后再从D中找到最小值，重复上述过程
时间复杂度：如果在D中寻找最小值用遍历法的话，时间复杂度是O(V2)
如果在D中寻找最小值用小顶堆的话，时间复杂度是O(E*logV)

Floyd算法

Floyd算法是计算多源最短路的算法，算法运行过程需要两个二位数组D和P分别记录从i到j的最短路长度，和j的父顶点
先用G的邻接矩阵初始化D。
然后使用一个三层for循环，对于每个临界点u，都用一个两层for循环试探以u作为中间节点是否能让v到w的距离更小，如果能得到更小的距离，则更新D。
时间复杂度O(V3)

查找算法

BST

BST的查找过程

我们可以递归地查找或迭代地查找：
递归：若key=val，则返回当前节点；若key>val，则转入右子树查找，否则转入左子树查找
迭代：while(root)，若key=val，则返回当前节点；若key>val，则令root=root->right，转入右子树查找，否则转入左子树查找

BST的删除过程

首先递归的查找要被删除的节点：设被删除的值为key，如果当前节点的值key，则转入左子树删除，如果=key，则找到了要被删除的节点。
删除节点时，如果当前节点没有孩子，或者只有一个孩子，这种情况是比较容易处理的，只需要将它的孩子返回给上一层的调用者用指针衔接上，这样就能保证有序性。反之，如果当前节点有两个孩子，我们可以用它右子树的最小值来覆盖掉当前节点，然后再把右子树的那个最小值删除，这样就能将问题转化为上面那种比较简单的删除情况。

BST的插入过程

先递归地查找正确的插入位置，若key>val，则转入右子树插入，否则转入左子树插入。直到遇到了NULL指针，此时malloc一个新节点，填充要插入的值，然后将该节点的地址返回给上一层调用者用指针衔接上。

AVL-Tree

AVL树的调整

当产生问题的节点在发现问题的节点的右子树的右子树，则进行RR旋转：将产生问题的父节点向上提，并让发现问题的节点作为其左子树
同理可以进行LL旋转。
当产生问题的节点在发现问题的节点的左子树的右子树，需要进行LR双旋，先将产生问题的节点向左上提，将其左子树挂到父节点上，把父节点挂在自己的左子树上；然后再将产生问题的节点向右上提，将其右子树挂到父节点的左子树上，把父节点挂到自己的左子树上
同理可进行RL双旋

RB-Tree

描述红黑树

红黑树是一种查找树，他的查找性能是O(logN)。与AVL树相比，RBT对节点的平衡性要求更弱一些，RBT允许最高的子树和最矮的子树高度相差2倍。
首先红黑树是一种BST，它要满足左<根<右的有序性。它的每个节点都会有一个颜色属性，红色或黑色，同时规定红黑树的根节点和叶子节点都是黑色的，而且从根节点到任意叶子节点经过的黑色节点数目都是相同的。红色节点的父节点和子节点都必须是黑色节点，也就是说在从根到叶的路径上不能连续出现两个红色节点。

B-Tree

描述B树和B+树

首先提出B树的目的是优化磁盘查找性能：对于磁盘这种块设备，读取1B和读取1KB所用的时间没有什么差别，所以我们在与磁盘交换信息时总是以块为单位的。在一个磁盘块中可以存储多个关键字，然后执行多路查找，也就构成了所谓的多路查找树，m路平衡搜索树就是所谓的m阶B树。
对于m阶B树，首先它是绝对平衡的，各个叶节点的深度相同。其次，它的内部节点的分支数最大为m，相应的，它的内部节点的关键码数量最大为m-1，这些关键码都是有序排列的。内部节点的分支数最小为m/2向上取整，但是树根节点的分支数最小可以为2。例如对于5阶B数，其内部节点分支数的范围为[3,5]

B+树的内部节点不保存数据，仅起到索引的作用。B+树的相邻叶子节点是通过指针连起来的，并且是按关键字大小排序的。B+树主要用于数据库的索引

排序算法

堆排序

描述堆这种数据结构

堆又称优先队列，它的逻辑结构是一棵完全二叉树，物理结构一般采用数组存储。堆可分为大顶堆和小顶堆，以大顶堆为例，对于其中的任何子树，其根节点都大于它的两个子节点，所以大顶堆的堆顶元素是堆中最大的元素。
以大顶堆为例，插入元素item时，首先将item放到数组的末尾，然后循环比较item是否大于它的父节点，如果大于，交换item和它的父节点，直到item小于它的父节点，此时就满足了堆的定义。
当我们删除堆顶元素时，我们需要用数组中的最后一个节点替换掉堆顶元素，然后比较它是否大于它的两个子节点，如果不大于，就与左右孩子中较大的值交换，重复此过程，直到它大于它的两个子节点，此时就满足了堆的定义。
如何将一个无序数组调整为堆：从最后一个有孩子的节点开始，将当前子树调整为堆（与左右孩子中较大的值交换），然后向前迭代，不断的将当前子树调整为堆，直到根节点。
建堆的时间复杂度：O(N)

快速排序

基础版：

int partition(int* arr,int left,int right){
	int pivot=arr[left];
	while(left<right){
		while(left<right&&arr[right]>=pivot){
			right--;
		}
		arr[left]=arr[right];
		while(left<right&&arr[left]<=pivot){
			left++;
		}
		arr[right]=arr[left];
	}
	arr[left]=pivot;
	return left;
}

void quick_sort(int* arr,int left,int right){
	if(left<right&&arr!=NULL){
		int p=partition(arr,left,right);
		quick_sort(arr,left,p-1);
		quick_sort(arr,p+1,right);
	}
}

计算机组成原理

数制和码制

CPU是怎么通过加法运算减法的

变补运算：所有位取反，末尾+1

中断

中断的响应过程

保存断点和程序状态
关中断（IF=0）
识别中断源并转入响应的中断处理程序

软中断：INT 0x80为系统调用

C语言

描述C语言过程调用过程

主调函数将参数从右向左压入栈，然后call被调函数（同时将返回地址压栈）
被调函数首先push ebp，将上一个函数栈帧的基址保存，然后mov esp,ebp，将当前的sp值作为当前函数栈帧的基址，然后sub sp一个值，开辟栈帧空间，再push需要保护的寄存器，最后通过ebp-4或ebp-8的形式取出传入的参数，接着进行处理
函数返回时要经过一系列pop恢复现场，返回值一般存放再eax中，然后执行ret指令返回主调函数

描述未赋值的全局变量和局部变量初值

这个问题我在gcc上尝试过，首先对于全局变量都会被初始化为0
对于局部变量，如果开O3优化的话，局部变量就会被赋值为0
如果不开优化的话，局部变量就是随机值

C++

描述C++的多态

多态的表现形式：父类中有虚函数；父类指针指向子类对象
如何实现多态：借助虚函数表，每个对象都有一个vtblptr，指向该类的虚函数表，如果子类重写了父类的虚函数，则其虚函数表的表项会指向自己那个函数的入口，实现了运行时多态
多态存在的意义：有多个不同的类，都带有同一个名称但具有不同实现的函数
多态的应用场景：工厂模式

描述指针和引用的区别

1. 引用在被创建时必须初始化，而指针可以在任何时候初始化
2. 不能有 NULL 引用，引用必须与合法的存储单元关联，而指针则可以是NULL
3. 函数的参数和返回值的传递方式有三种：值传递、指针传递和引用传递。
4. 有指针数组，但是不能有引用数组
5. 引用相比于指针使用起来更简单清楚，使得C++程序不必像C语言程序那样满屏的*号
6. 指针有自己的一块空间，而引用只是一个别名

描述面向过程和面向对象的区别

面向过程的的开发过程，就是一层层的函数调用过程，它更符合计算机本身的工作逻辑，因此效率比面向对象高。
而面向对象是把问题分解成一个个的对象，让每一个对象去解决不同的子问题。
面向对象具有三大特性：封装，继承和多态；
封装实现了对信息的隐藏和对客观事物的抽象
继承实现了代码的复用。而且在增加新需求时，只需多派生一个子类即可实现，无需修改已经测试好的代码
多态通过让父类指针指向子类对象，赋值之后，父对象就可以根据当前赋值给它的子对象的特性以不同的方式运作。
面向对象的编程方式使得每一个类都只做一件事，这样当需求发生变动时修改代码很容易。而面向过程会让一个类越来越全能，就像一个管家一样做了所有的事，需求变动时我们必须修改原有的代码，并重新测试

STL

map

map是stl中的一个关联式容器，底层采用红黑树实现。他的模板参数有两个，分别指定键和值的类型。插入的数据类型是pair类型，当用迭代器访问map中的元素时，iter->first可以取出第一个元素，iter->second可以取出第二个元素。

map 容器存储多个键值对时，该容器会自动根据各键值对的键的大小，按照既定的规则进行排序。使用 map 容器存储的各个键值对，键的值既不能重复也不能被修改。

map<string, int> myMap{ {"C语言教程",10},{"STL教程",20} };

myMap.emplace({"halo",30});
myMap.insert({"hello",40});

//输出当前 myMap 容器存储键值对的个数
cout << "myMap size==" << myMap.size() << endl;
//判断当前 myMap 容器是否为空
if (!myMap.empty()) {
    //借助 myMap 容器迭代器，将该容器的键值对逐个输出
    for (auto i = myMap.begin(); i != myMap.end(); ++i) {
        cout << i->first << " " << i->second << endl;
    }
} 

unordered_map

unordered_map 容器和 map 容器仅有一点不同，即 map 容器中存储的数据是有序的，而 unordered_map 容器中是无序的。

set

set也属于有序关联式容器，和 map、multimap 容器不同，使用 set 容器存储的各个键值对，要求键 key 和值 value 必须相等。

//创建空set容器
std::set<std::string> myset;
//空set容器不存储任何元素
cout << "1、myset size = " << myset.size() << endl;
//向myset容器中插入新元素
myset.insert("http://c.biancheng.net/java/");
myset.insert("http://c.biancheng.net/stl/");
myset.insert("http://c.biancheng.net/python/");
cout << "2、myset size = " << myset.size() << endl;
//利用双向迭代器，遍历myset
for (auto iter = myset.begin(); iter != myset.end(); ++iter) {
    cout << *iter << endl;
}

unordered_set

unordered_set 容器和 set 容器很像，唯一的区别就在于 set 容器会自行对存储的数据进行排序，而 unordered_set 容器不会。

无序容器的底层实现原理为采用链地址法来避免碰撞的哈希表

unordered_set uset{ "hello", "world", "hola" };

uset.insert("fuck");
uset.emplace("you");

for (auto iter = uset.begin(); iter != uset.end(); ++iter) {
    cout << *iter << endl;
}

设计模式

软件工程

软件的生命周期

问题定义，可行性分析，需求分析，开发，维护

软件过程

瀑布模型：类似于链表，把软件过程分为不同的阶段，只有当上一个阶段完成才能进入下一个阶段，否则返回重做。编码过程被推迟到后面实现
快速原型模型：先建立起一个能够反映用户原型系统，在实践中明确用户的需求
增量模型：将软件分解为一些增量构件，分阶段向用户提交更为完善的软件产品
螺旋模型：考虑了软件开发过程中的风险，在进行每一个开发周期之前都要评估风险
喷泉模型：改进了瀑布模型，在每一个设计编码测试阶段都进行迭代，以实现精益求精的过程