单调队列优化DP

模型

求一段区间(窗口)最值的时候，当然这个窗口不需要固定大小，只要保证首尾是递增的即可；

见经典模型滑动窗口；

如何使用

1. 按照常规DP思路定义好状态，写好转移方程(保证正确性)
2. 和其他优化方式一样，对转移方程做等价变换；

例题

最大子序和

题面

思路

时间复杂度是$O(n)$的；

注意一个点，子序列的长度不能为空！！

因此我们滑动窗口的右边框是当前点$i$往左边移动一个位置；

Code

#include 
#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;
struct Node{
	int val,idx;
};
const int N = 300000 + 10;
int s[N];//前缀和
int f[N];//这里f(i)其实没有必要，但是方便理解；
//用一个变量来代替即可，彼此之间没有递推关系
void solve(){
	int n,k;
	cin >> n >> k;
	for(int i=1;i<=n;++i)
		cin >> s[i],s[i] += s[i-1];
	deque<Node> dq;//维护最小值
	for(int i=0;i<=n;++i){//注意这里要取0，因为要计算前缀和
		while(!dq.empty()&&dq.front().idx < i-k) dq.pop_front();
		if(!dq.empty()) f[i] = s[i] - dq.front().val;
		while(!dq.empty()&&dq.back().val>=s[i]) dq.pop_back();
		dq.push_back({s[i],i});
	}
	ll ans = -1e18;
	for(int i=1;i<=n;++i) ans = max(ans,1ll*f[i]);
	cout << ans << '\n';
}

signed main(){
	std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	solve();
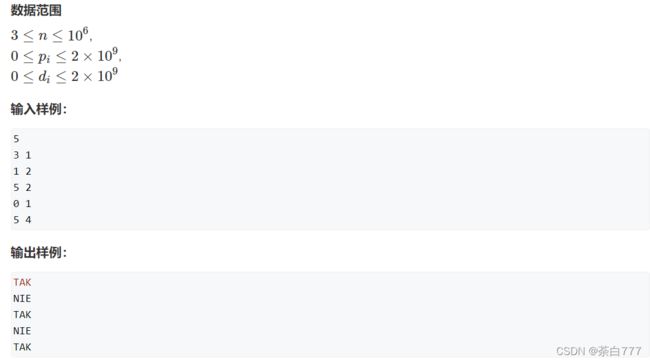
	return 0;
}

旅行问题

传送门

题面

思路

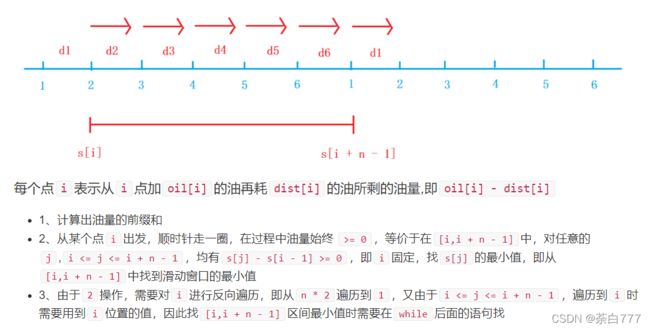
首先断环为链，问题就变成线性的了；

这里讲一下为什么顺时针需要逆序遍历，因为我们是要计算下面这个式子；

$min(s_j-s_i)$，提出常数则有$min(s_j)-s_i$

如果我们是从前往后，那么我们更新前面的点不一定是最优的，它需要后面的点来更新；

这就是为什么这道题是DP了，你需要考虑DP的拓扑序；

---

或者你简单的记忆，例题一最大子序和，是前面一项不变，后面一项最小，那么就是从前往后；

本题是后面一项不变，前面一项最小，那么就是从后往前；

---

逆序的情况和正序对称即可；

Code

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

#define int ll

const int N = 1e6 + 10;
int p[N],d[N];
ll s[N<<1];//前缀和
int dq[N<<1];//双端队列，存的是下标
bool st[N];
void solve(){
	int n;
	cin >> n;
	for(int i=1;i<=n;++i){
		cin >> p[i] >> d[i];
	}
	//先处理顺时针
	for(int i=1;i<=n;++i)
		s[i] = p[i] - d[i],s[i+n] = s[i];
	for(int i=1;i<=2*n;++i)
		s[i] += s[i-1];
	int hh = 0,tt = -1;//模拟双端队列 比deque快
	//注意递推顺序
	for(int i=2*n;i>=0;--i){
		while(hh <= tt&&dq[hh] > i+n-1) ++hh;
		if(hh <= tt && i < n)
			st[i+1] = (s[dq[hh]] - s[i]) >= 0;
		while(hh <= tt &&s[dq[tt]] >= s[i]) --tt;
		dq[++tt] = i;
	}
	//处理逆时针
	d[0] = d[n];//注意下面的d(i-1)会用到d(0)
	for(int i=1;i<=n;++i){
		s[i] = s[i+n] = p[i] - d[i-1];
	}
	for(int i=2*n;i>=1;--i)
		s[i] += s[i+1];
	hh = 0,tt = -1;
	for(int i=1;i<=2*n+1;++i){
		while(hh <= tt && i-n+1 > dq[hh]) ++hh;
		if(hh <= tt && i > n+1)
			st[i-1] = (s[dq[hh]] - s[i]) >= 0;
		while(hh <= tt && s[dq[tt]] >= s[i]) --tt;
		dq[++tt] = i;
	}
	for(int i=1;i<=n;++i) st[i] |= st[i+n];
	for(int i=1;i<=n;++i){
		puts(st[i]?"TAK":"NIE");
	}
}

signed main(){
	solve();
	return 0;
}

烽火传递

传送门

题面

思路

Code

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 2e5 + 10;
int f[N],a[N],dq[N];//f(i)表示前i个烽火台能正常传递信息，且点燃第i个的最小代价
void solve(){
	int n,m;
	cin >> n >> m;
	for(int i=1;i<=n;++i){
		cin >> a[i];
		f[i] = 1e9;
	}
	int hh = 0,tt = -1;
	//f[0] = 0
	for(int i=0;i<=n;++i){
		while(hh <= tt && dq[hh] < i-m) ++hh;
		if(hh <= tt) f[i] = a[i] + f[dq[hh]]; 
		while(hh <= tt && f[dq[tt]] >= f[i]) --tt;
		dq[++tt] = i;
	}
	int ans = 1e9;
	for(int i=n-m+1;i<=n;++i)
		ans = min(ans,f[i]);
	cout << ans;
}

signed main(){
	std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	solve();
	return 0;
}

绿色通道

传送门

题面

思路

首先看到最大值最小，考虑一下二分；

下图中的m指的是题中的时间t

转换完以后，这道题就变成了上一题，注意一下边界即可

Code

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 5e4 + 10;

int n,t;
//f[i]表示写第i道题目，且前i道题目中最长空格数量不超过k的所有方案中的最小花费时间
int a[N],f[N],dq[N];
bool ck(int k){
	int hh = 0,tt = -1;
	for(int i=1;i<=n;++i) f[i] = 1e9;
	//f[0] = 0
	for(int i=0;i<=n;++i){
						//第i个点不空，至多空k个，那么极限就是i-k-1不能空
		while(hh <= tt && dq[hh] < i-k-1) ++hh;
		if(hh <= tt) f[i] = f[dq[hh]] + a[i];
		while(hh <= tt && f[dq[tt]] >= f[i]) --tt;
		dq[++tt] = i;
	}
	int res = 1e9;
	//至多k个空，那么从n-k开始取就行
	for(int i=n-k;i<=n;++i)
		res = min(res,f[i]);
	return res <= t;
}
void solve(){
	cin >> n >> t;
	for(int i=1;i<=n;++i)
		cin >> a[i];
	int l = 0,r = n;
	while(l<r){
		int mid = (l+r)>>1;
		if(ck(mid)) r = mid;
		else l = mid + 1;
	}
	cout << l;
}

signed main(){
	std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	solve();
	return 0;
}

修建草坪

传送门

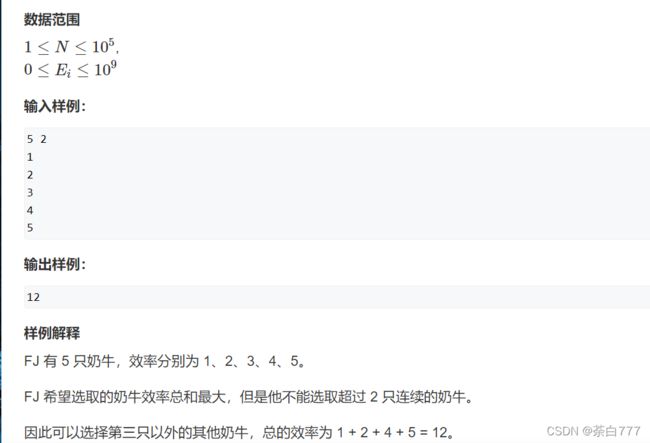
题面

思路

我们用f(i)表示前i头牛能组成的最大效率值

如果不选第$i$头牛，那么有f(i) = f(i-1)

如果选择第$i$头牛，因为题意要求我们至多连续选$k$头牛；

那么我们可以选$j\in [1...k]$头牛，为了保证是$j$头牛，那么要保证i-j这个位置一定不能取；

则有f(i) = s(i) - s(i-j) + f(i-j-1)，要保证第$i-j$头牛不能取；

因为要保证最大，则有$f(i)=s(i)+max\{f(i-j-1)-s(i-j)\}$

注意一下当$i=j$的时候，会访问到$f(-1)$，前-1头牛没有意义，取$0$即可；

然后令$x=i-j$，则上式变为$f(i)=s(i)+max\{f(x-1)-s(x)\}$

我们用单调队列维护后面这个式子($max\{f(x+1)-s(x)\}$)；

其中s(i)表示前缀和

Code

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;
int a[N],dq[N];
ll s[N],f[N];
ll g(int x){//x表示的是一个位置
	//g(x) = f(x-1) - s(x)
	if(x == 0) return 0;
	return f[x-1] - s[x];
}
void solve(){
	int n,k;
	cin >> n >> k;
	for(int i=1;i<=n;++i)
		cin >> a[i],s[i] = s[i-1] + a[i];
	//取一个0用来表示当i=j的时候
	int hh = 0,tt = 0;
	for(int i=1;i<=n;++i){
	//这里i-k是因为我们看初始的式子s(i)-s(i-j)+f(i-j-1),j是可以取到k的
	//现在我们把i-j看成一个坐标x，那么这个坐标左边界是i-k(包含的,当j=k时)
		while(hh <= tt && dq[hh] < i-k) ++hh;
		f[i] = f[i-1];
		if(hh <= tt)
			f[i] = max(f[i],s[i] + g(dq[hh]));
		while(hh <= tt && g(dq[tt]) <= g(i)) --tt;
		dq[++tt] = i;
	}
	cout << f[n];
}

signed main(){
	std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	solve();
	return 0;
}

理想正方形

传送门

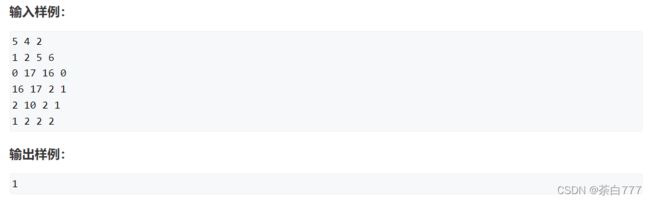
题面

思路

这题其实不是个DP，而是滑动窗口问题的扩展，因此也拿过来了；

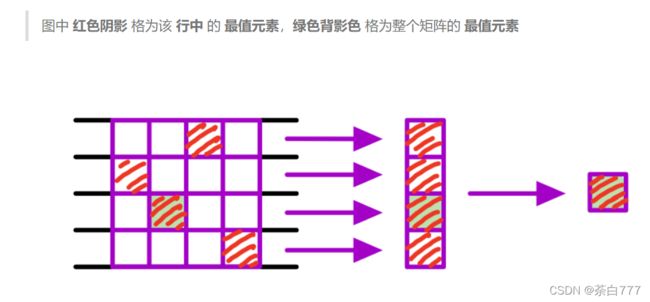
首先对于每个格子，我们预处理它往左连续$k$个的最值；

对于这些处理出来的最值，对于每个点，我们处理出它往上连续$k$个的最值；

不难想到，这些处理最值的过程就用滑动窗口模型来解决；

然后相减输出答案即可；

Code

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 1e3 + 10;

int n,m,k,dq[N];
int G[N][N];
int row_mx[N][N],row_mn[N][N];
//f(i)存放结果
void get_mx(int a[],int f[],int len){
	int hh = 0,tt = -1;
	for(int i=1;i<=len;++i){
		while(hh <= tt && dq[hh] < i-k+1) ++hh;
		while(hh <= tt && a[dq[tt]] <= a[i]) --tt;
		dq[++tt] = i;
		f[i] = a[dq[hh]];
	}
}
void get_mn(int a[],int f[],int len){
	int hh = 0,tt = -1;
	for(int i=1;i<=len;++i){
		while(hh <= tt && dq[hh] < i-k+1) ++hh;
		while(hh <= tt && a[dq[tt]] >= a[i]) --tt;
		dq[++tt] = i;
		f[i] = a[dq[hh]];
	}
}
void solve(){
	cin >> n >> m >> k;
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m;++j)
			cin >> G[i][j];
	//预处理每个位置往左探长度为k的最值
	for(int i=1;i<=n;++i){
		get_mx(G[i],row_mx[i],m);
		get_mn(G[i],row_mn[i],m);
	}
	int a[N],mx[N],mn[N];
	//枚举右边界
	int ans = 1e9;
	for(int r=k;r<=m;++r){
		for(int i=1;i<=n;++i) a[i] = row_mx[i][r];
		get_mx(a,mx,n);
		for(int i=1;i<=n;++i) a[i] = row_mn[i][r];
		get_mn(a,mn,n);
		for(int i=k;i<=n;++i)
			ans = min(ans,mx[i] - mn[i]);
	}
	cout << ans << '\n';
}

signed main(){
	std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	solve();
	return 0;
}

其他例题

单调队列优化多重背包