二叉搜索树删除操作的递归与非递归写法

如何进行删除操作

对于二叉搜索树的删除操作，主要分为以下3种情况讨论：

1、删除的结点没有左右孩子

2、删除的结点只有一个孩子

3、删除的结点有左右孩子

所以，我们将会用if…else…分为最多3种情况讨论（实际上只分了两种，因为情况1、2可以合并为一种情况）

---

删除操作的非递归写法

对于情况1、2：由于删除结点之后，有唯一（或nullptr）的结点来接手被删除的结点的位置（且该节点接手后不会破坏二叉搜索树），所以这两种情况的删除操作很容易实现

由于两边都为空的情况比较特殊，所以就做了一些处理：

将两边都为空的情况视为右孩子是nullptr，左孩子不确定 ，被删除的结点直接替换成左孩子（由于左孩子是nullptr，所以替换之后并无影响）

if (cur->_right == nullptr)//对于右孩子为空和左右孩子都为空的情况都会满足判断条件
{
    if (cur == _root)//对于根情况需要做额外判断
    {
        _root = cur->_left;
    }
    else if (parent->_left == cur)
    {
        parent->_left = cur->_left;
    }
    else
    {
        parent->_right = cur->_left;
    }
    delete cur;
    return true;
}
else if (cur->_left == nullptr)
{
    if (cur == _root)
    {
        _root = cur->_right;
    }
    else if (parent->_left == cur)
    {
        parent->_left = cur->_right;
    }
    else
    {
        parent->_right = cur->_right;
    }
    delete cur;
    return true;
}

对于情况3：由于删除结点之后，左右孩子（甚至其它结点）都有可能代替被删除结点，倘若直接替换，则会破坏该二叉搜索树。所以需要单独讨论

处理方法有两种，这里讨论其中一种

上图将5结点删除后，用x替代其位置：
如果用x替代5的位置，根据二叉搜索树的性质，有x>2，x<7，保证了删除后的二叉树还是二叉搜索树。

而这个x是被删除结点右子树的最左的孩子 ：从被删除结点的右孩子开始，一直找左孩子，直到空为止。

Node* rightMinparent = cur;//记录右子树的最小结点的父节点，用来确保其替换删除结点后，还能继续链接最小结点的右子树
Node* rightMin = cur->_right;
while (rightMin->_left != nullptr)//寻找最小结点
{
    rightMinparent = rightMin;//记录最小结点的父节点
    rightMin = rightMin->_left;
}
cur->_key = rightMin->_key;//交换被删除结点和最小结点的值
if (rightMinparent->_left == rightMin)//链接最小结点的右子树
    rightMinparent->_left = rightMin->_right;
else
    rightMinparent->_right = rightMin->_right;
delete rightMin;//释放被删除节点的空间（因为交换了值，所以此时该结点是被删除结点）
return true;

---

删除操作的递归写法

递归的整体思路与上述一致，只是对情况3的操作略有不同

• 若结点为空，则返回
• 若结点不是要删除结点，则递归其左右
• 若结点是要删除结点，则执行删除操作

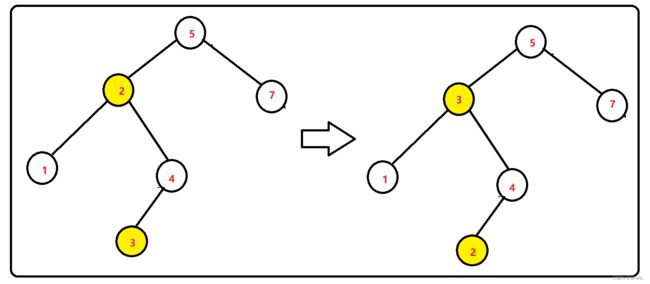
其中，对于情况3的删除操作做了如下处理：

如上图所示，在删除结点2时，并没有直接对其进行delete操作，而是将其与最小值结点进行了值交换，然后再递归过去删除最小值结点。

if (root == nullptr)
    return false;
if (root->_key > key)
{
    _EraseR(root->_left, key);//递归左子树
}
else if (root->_key < key)
{
    _EraseR(root->_right, key);//递归右子树
}
else
{
    Node* cur = root;
    if (root->_right == nullptr)//情况1、2
    {
        root = root->_left;
    }
    else if (root->_left == nullptr)
    {
        root = root->_right;
    }
    else//情况3
    {
        Node* rightMin = root->_right;
        while (rightMin->_left)
        {
            rightMin = rightMin->_left;
        }
        swap(root->_key, rightMin->_key);//交换值
        return _EraseR(root->_right, key);//继续递归
    }
    delete cur;//释放情况1、2的被删除结点的空间
    return true;
}