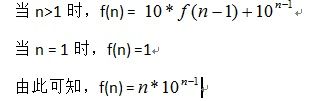c语言 火柴加法,C语言程序设计100例之（18）：火柴棒等式

例18   火柴棒等式

用n根火柴棍，可以拼出多少个形如“A+B=C”的等式？等式中的A、B、C是用火柴棒拼出的整数(若该数非零，则最高位不能是0)。用火柴棒拼数字0~9的拼法如图1所示。

图1  用火柴棒拼的数字0~9

另外，加号与等号各自需要两根火柴棒。

编写一个程序，输入火柴棒的根数n，输出能拼成的不同等式的数目。说明：(1)如果A≠B，则A+B=C与B+A=C视为不同的等式(A、B、C>=0)；(2)A和B最多为3位数；(3)n根火柴棒必须全部用上。

例如，输入18，输出应为9。即18根火柴棒可以拼出0+4=4、0+11=11、1+10=11、2+2=4 、2+7=9、4+0=4、7+2=9、10+1=11、11+0=11这9个等式。

(1)编程思路1。

用一个数组保存0~9每个数字所需火柴棒数，另外加号和等号需用去4根。

编写一个函数int needMatch(int num)用于统计数 num 需要的火柴棒个数。

程序中用二重循环对A(0~999)和B(0~999)的取值组合进行穷举，调用函数needMatch(A)、needMatch(B)和needMatch(A+B)分别返回等式中三个数所需的火柴棒的数目，若needMatch(A)+needMatch(B)+needMatch(A+B)+4==n，则计数。

(2)源程序1。

#include

int needMatch(int num);   // 统计数 num 需要的火柴棒个数

int main()

{

int n,i,j,sum1,sum2,sum3,cnt;

scanf("%d",&n);

cnt=0;

for(i=0;i<1000;i++)

for(j=0;j<1000;j++)   // 二重循环枚举两个加数

{

sum1=needMatch(i);

sum2=needMatch(j);

sum3=needMatch(i+j); // 分别求出两个加数和一个和分别需要的火柴棒

if(sum1+sum2+sum3+4==n)

cnt++;

}

printf("%dn",cnt);

return 0;

}

int needMatch(int num) // 统计数 num 需要的火柴棒个数

{

int table[10]={6,2,5,5,4,5,6,3,7,6};

int sum=0;

if(num==0)         // 数0 特殊处理

return(6);

else

{

while(num!=0)

{

sum+=table[num%10];  // 分解出每一位并加上此位的火柴棒个数

num=num/10;          // 准备处理下一位

}

return(sum);

}

}

(3)编程思路2。

编程思路1中调用一个函数needMatch来返回每个数字num所需火柴棒数，在穷举时，这个函数会被调用1000*1000*3=3000000(3百万次)，程序执行速度较慢。下面采用以空间换时间的方法，提高程序的执行速度。

由于等式中可能出现的数在0~1998之间，因此可以定义一个数组int needmatch[1999]，保存拼出0~1998每个数字所需要的火柴棒数，needmatch[i]的值为拼出数字i所需的火柴棒数。这样，先计算好数组中的每个元素的值后，在对等式中数A和B进行穷举时，等式中三个数所需的火柴棒数只需直接引用数组元素的值即可。相当于思路1中的needMatch函数只调用了1999次，因此程序的运行速度会大大提高。

(4)源程序2。

#include

int main()

{

int n,i,j,cnt;

int match[10]={6,2,5,5,4,5,6,3,7,6};  // 定义0~9每个数字所需要的火柴棒数

int needmatch[2000];     // 保存拼出0~1999每个数字所需要的火柴棒数

scanf("%d",&n);

for (i=0;i<=9;i++)

needmatch[i]=match[i];

for (i=10;i<2000;i++)     // 计算10~1999中每个数需要的火柴棒数目

{

if (i<100)           //  10~99 两位数

needmatch[i]=match[i/10]+match[i%10];

else if (i<1000)      //  100~999 三位数

needmatch[i]=match[i/100]+match[i/10%10]+match[i%10];

else               //  1000~1999  四位数

needmatch[i]=match[i/1000]+match[i/100%10]+match[i/10%10]+match[i%10];

}

cnt=0;

for(i=0;i<1000;i++)

for(j=0;j<1000;j++)   //二重循环枚举两个加数

if(needmatch[i]+needmatch[j]+needmatch[i+j]+4==n)

cnt++;

printf("%dn",cnt);

return 0;

}

习题18

18-1  计数问题

本题选自洛谷题库 (https://www.luogu.org/problem/P1980)

题目描述

试计算在区间 1 到 n的所有整数中，数字 x(0 ≤ x ≤ 9)共出现了多少次？例如，在 1到 11中，即在 1,2,3,4,5,6,7,8,9,10,11中，数字 1 出现了 4 次。

输入格式

2个整数n,x，之间用一个空格隔开。

输出格式

1个整数，表示x出现的次数。

输入样例

11 1

输出样例

4

(1)编程思路1。

定义一个数组count[10]，元素count[0]~count[9]分别保存数字0~9在全部n个整数中用到的次数。初始值全为0，表示开始时每个数字均没用到。

程序可以写成一个循环，框架为：

for (i=1； i<=n ；i++)

{

对每个整数i，依次分离出i的各位数字k，对应的count[k]++；

}

对于整数i，分离出各位数字的操作为：不断除以10，记下余数，直到商为0。所得余数序列就是整数i从低位到高位的各位数字。具体描述为：

while (i)

{    count[ i %10] ++;

i=i/10;

}

(2)源程序1。

#include

int main()

{

int n,i,t,x;

int count[10] = {0};

scanf("%d%d",&n,&x);

for(i = 1; i <= n; i++)

{

t = i;

while(t)

{

count[t%10]++;      t/=10;

}

}

printf("%dn",count[x]);

return 0;

}

(3)编程思路2。

程序1中n个整数各个数字的统计用一个二重循环完成，外循环处理n个整数，内循环处理n的每位数字，n的数字位数为log10n+1，所以这个算法的时间复杂度为O(n*log10n)。

下面我们给出一种更高效解决这个问题的方法。

1)考察由0、1、2、…、9十个数字组成的所有n位数。从n个0到n个9共有10n个n位数。在这10n个n位数中，0、1、2、…、9这十个数字使用次数相同，设为f(n)。f(n)满足如下递推式：

2)对于一个m位整数，我们可以把0到n之间的n+1个整数从小到大这样来排列：

000……0

…………

099……9

100……0

…………

199……9

…………

这样一直排到自然数n。对于从0到099……9这个区间来说，抛去最高位的数字不看，其低m-1位恰好就是m-1个0到m-1个9共个数。利用上面的递推公式，在这个区间里，每个数字出现的次数(不包括最高位数字)为。假设n的最高位数字是x，那么在n之间上述所说的区间共有x个。那么每个数字出现的次数x倍就可以统计完这些区间。再看最高位数字的情况，显然0到x-1这些数字在最高位上再现的次数为，因为一个区间长度为；而x在最高位上出现次数就是。接下来对，即n去掉最高位后的那个数字再继续重复上面的方法。直到个位，就可以完成各个数字的统计了。

比如，对于一个数字3482，我们可以这样来计算从1到3482之间所有数字中每个数字出现的次数。

从0到999，这个区间的每个数字的出现次数可以使用前面给出的递推公式，即每个数字出现400次。从1000到1999，中间除去千位的1不算，又是一个从000到999的排列，这样的话，从0到3482之间的这样的区间共有3个。所以从0000到2999之间除千位外，每个数字(0~9)出现次数均为3*400次。

然后再统计千位数字，每个区间长度为1000，所以0、1、2在千位上各出现1000次。而3则出现482+1=483次。

之后，抛掉千位数字，对于482，再使用上面的方法计算，一直计算到个位即可。

(4)源程序2。

#include

#include

int main()

{

int n,x,i,len,m,k,h;

int pow10[10] = {1}, count[10] = {0};

char d[11];

for(i = 1; i < 10; i++)

{

pow10[i] = pow10[i-1] * 10;

}

scanf("%d%d",&n,&x);

len = log10(n);         // len 表示当前数字的位权,一个5位数，

// 最高位权为10的4次方，len=4

m = len;

sprintf(d, "%d", n);      // 将数n 转换为字符串存入数组d中

k = 0;                //  k 存储当前最高位数字在d数组中的下标

h = d[k] - '0';           //  h 存储当前最高位的数字

n %= pow10[len];      //  去掉n的最高位

while(len > 0)

{

if(h == 0)         // 当前数字如果为0

{

count[0] += n + 1;       h = d[++k] - '0';

len--;                 n %= pow10[len];

continue;

}

for(i = 0; i < 10; i++)

count[i] += h * len * pow10[len-1];   //

for(i = 0; i < h; i++)        // 最高位0~h-1出现次数

count[i] += pow10[len];

count[h] += n + 1;            // 最高位 h 出现次数

len--;          h = d[++k] - '0';

n %= pow10[len];              // n 抛掉最高位

}

for(i = 0; i <= h; i++)          // 个位上0~h出现次数

count[i] += 1;

for(i = 0; i <= m; i++)          //  减去前导0的个数

count[0] -= pow10[i];

printf("%dn",count[x]);

return 0;

}

18-2  三连击

本题选自洛谷题库 (https://www.luogu.org/problem/P1008)

题目描述

将1,2,⋯,9共9个数分成3组，分别组成3个三位数，且使这3个三位数构成1:2:3的比例，试求出所有满足条件的3个三位数。

输入格式

没有输入

输出格式

若干行，每行3个数字。按照每行第1个数字升序排列。

输入样例

无

输出样例

192  384  576

* * *

...

* * *

(输出被和谐了)

(1)编程思路1。

三个三位数，一共9个位，可以将每一个数位为枚举对象，一位一位地去枚举。

定义9个整型变量A、B、C、D、E、F、G、H、I分别表示三个数的9个位，每个变量取1~9之间的一个值。如ABC表示第1个数x、DEF表示第2个数y，GHI表示第3个数z。

根据A~I的具体取值，可以计算x、y、z，三个数需要满足条件2*x==y && 3*x==z(构成1：2：3的比例)；另外，还得考虑A~I各个数位的数字取值不相同，为确保9个变量取值各不相同，只要同时满足A+B+C+D+E+F+G+H+I==45(1+2+3+4+5+6+7+8+9=45)和A*B*C*D*E*F*G*H*I==362880(1*2*3*4*5*6*7*8*9=362880)即可。

(2)源程序1。

#include

int main()

{

int a,b,c,d,e,f,g,h,i,x,y,z;

for (a=1;a<=9;a++)

for (b=1;b<=9;b++)

for (c=1;c<=9;c++)

for (d=1;d<=9;d++)

for (e=1;e<=9;e++)

for (f=1;f<=9;f++)

for (g=1;g<=9;g++)

for (h=1;h<=9;h++)

for (i=1;i<=9;i++)

{

x=a*100+b*10+c;

y=d*100+e*10+f;

z=g*100+h*10+i;

if (a+b+c+d+e+f+g+h+i==45  && a*b*c*d*e*f*g*h*i==362880

&& 2*x==y && 3*x==z)

printf("%d %d %dn",x,y,z);

}

return 0;

}

(3)编程思路2。

按程序1的思路，穷举次数有99次，如果分别设三个数为x、2x和3x，以x为枚举对象，则x的最小值为123、最大值为329(因为下一个数341*3=1023>987)，穷举的范围就减少为107。

由于对x进行穷举，因此需要将3个三位数的各个位上的数字分离出来。这9个数字可以像程序1中一样，用A~I这9个变量来保存。在程序2中，我们采用另外一种方法。定义一个一维数组a[9]，把组成整数x、2x、3x的9个数字存放在数组a中。然后用一个二重循环统计1~9这9个数字是否全在数组中出现。

(4)源程序2。

#include

int main()

{

int a[9],x,cnt,i,j,flag;

for (x=123;x<=329;x++)        // 枚举所有可能的解

{   // 把组成整数x、2x、3x的9个数字存放在数组a中

a[0]=x/100;  a[1]=x/10%10;  a[2]=x%10;

a[3]=(2*x)/100;  a[4]=(2*x)/10%10;  a[5]=(2*x)%10;

a[6]=(3*x)/100;  a[7]=(3*x)/10%10;  a[8]=(3*x)%10;

cnt=0;

for (i=1;i<=9;i++)    // 检查1~9这9个数字是否都在a中

{

flag=-1;

for (j=0;j<9;j++)

if (i==a[j])

{   flag=j; break;  }

if (flag!=-1)

cnt++;

else

break;   // 如果有数字不在a中，则退出循环

}

if (cnt==9)

printf("%d %d %dn",x,x*2,x*3);

}

return 0;

}

18-3  三连击(升级版)

本题选自洛谷题库 (https://www.luogu.org/problem/P1618)

题目描述

将1，2，…，9共9个数分成三组，分别组成三个三位数，且使这三个三位数的比例是A:B:C，试求出所有满足条件的三个三位数，若无解，输出“No!!!”。

输入格式

三个数，A B C(A

输出格式

若干行，每行3个数字。按照每行第一个数字升序排列。

输入样例

1 2 3

输出样例

192  384  576

219  438  657

273  546  819

327  654  981

(1)编程思路。

分别设三个数为x1、x2和x3，以x1为枚举对象，计算出x2和x3(x2=b*x1/a;  x3=c*x1/a)，且x1的最小值为123、最大值为987*a/c(x3最大为987)。

由于对x1进行穷举，因此需要判断1~9这9个数字是否全在x1、x2和x3这三个数中出现。为此定义一个数组hash[10]，其中hash[i]的值代表数字i(0<=i<=9)在3个三位数中出现的次数，每次穷举前hash数组的元素值全为0。若穷举某个x1时，hash[1]~hash[9]的值全为1，则表示1~9这9个数字全在三个数中出现了，得到一组解。

(2)源程序。

#include

int main()

{

int hash[10],x1,x2,x3,a,b,c,i,flag=0;

scanf("%d%d%d",&a,&b,&c);

for (x1=123;x1<=987*a/c;x1++)        // 枚举所有可能的解

{

for (i=0;i<=9;i++) hash[i]=0;

x2=b*x1/a;  x3=c*x1/a;

hash[x1/100]++;  hash[x1/10%10]++;  hash[x1%10]++;

hash[x2/100]++;  hash[x2/10%10]++;  hash[x2%10]++;

hash[x3/100]++;  hash[x3/10%10]++;  hash[x3%10]++;

for (i=1;i<=9;i++) // 检查1~9这9个数字是否都出现

if (hash[i]!=1) break;

if (i>9)

{

printf("%d %d %dn",x1,x2,x3);

flag=1;

}

}

if (flag==0)  printf("No!!!n");

return 0;

}

内容来源于网络如有侵权请私信删除