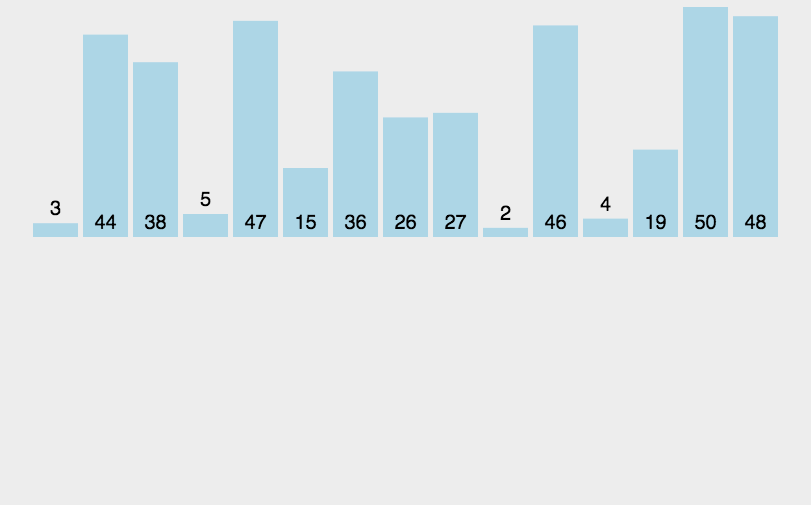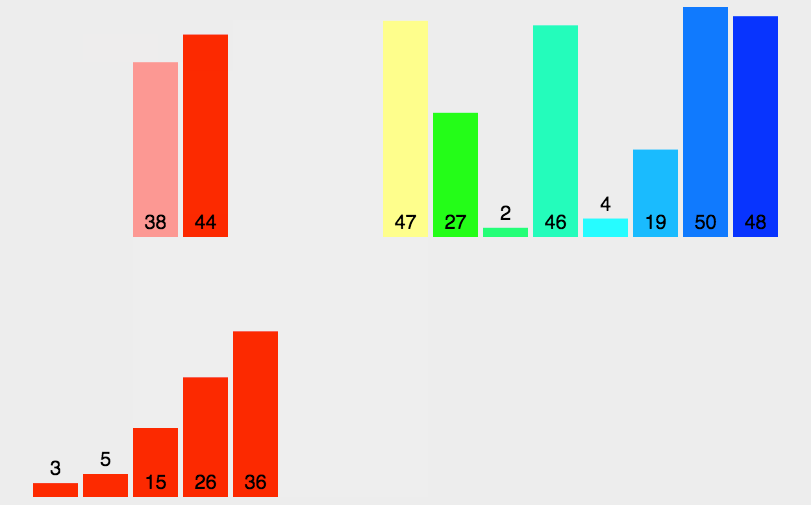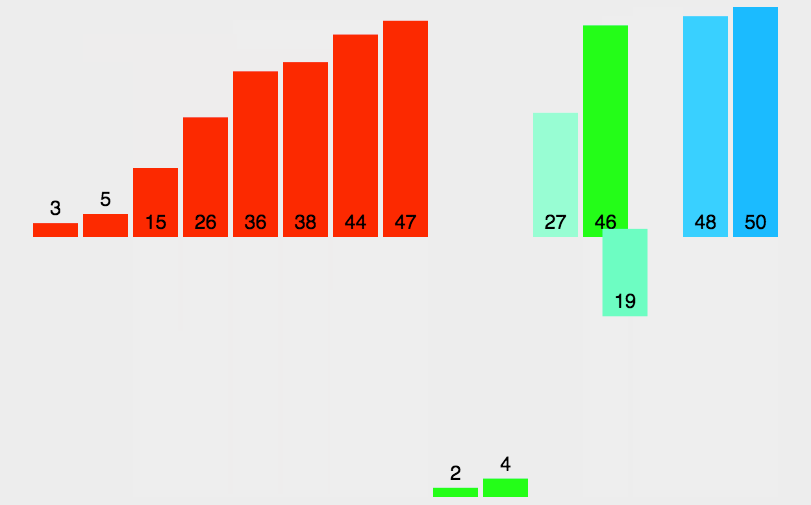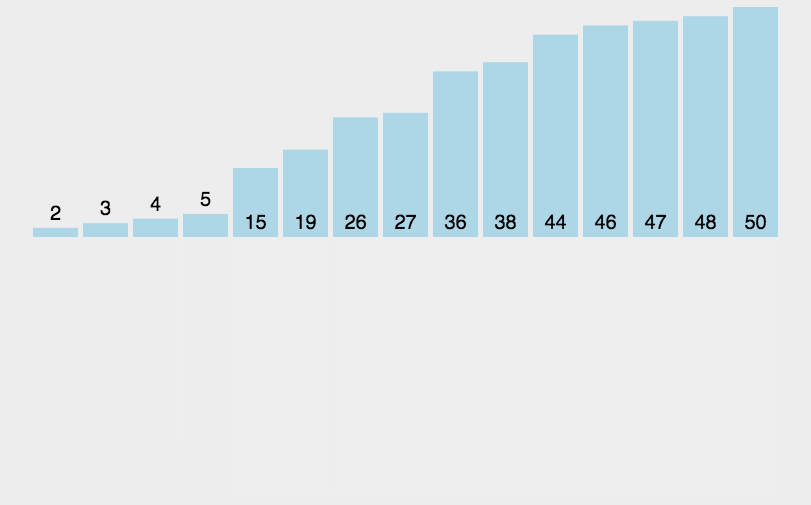
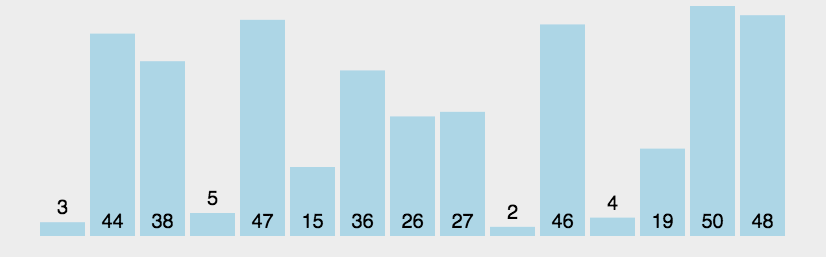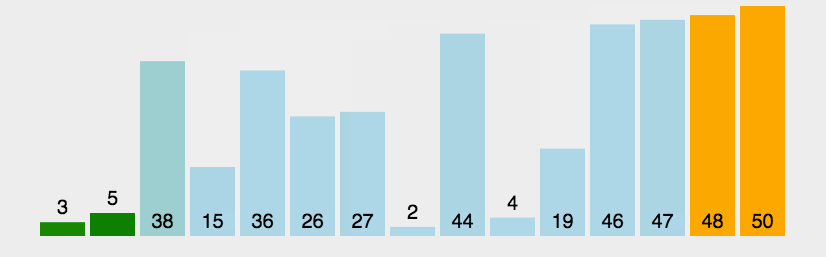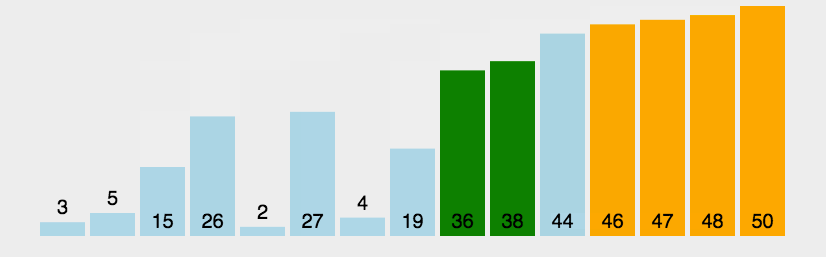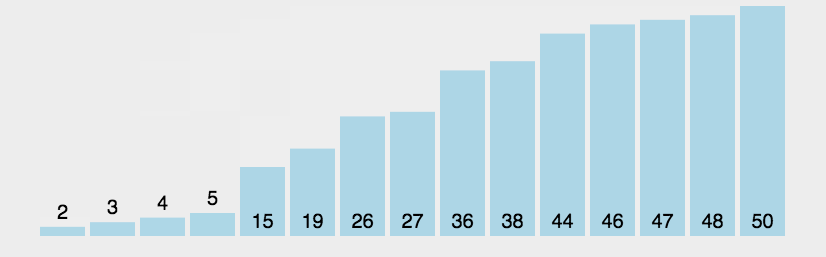常用经典排序算法
排序算法
本文主要介绍常用的经典排序算法
内容
重点排序算法主要分为：交换【1、2】、插入【3、4】、选择【5、6】、归并、计数排序、桶排序、基数排序 其中：1、冒泡排序
2、快速排序
3、简单插入排序
4、希尔排序
5、简单选择
6、堆排序
7、归并排序
8、计数排序
9、桶排序
10、基数排序
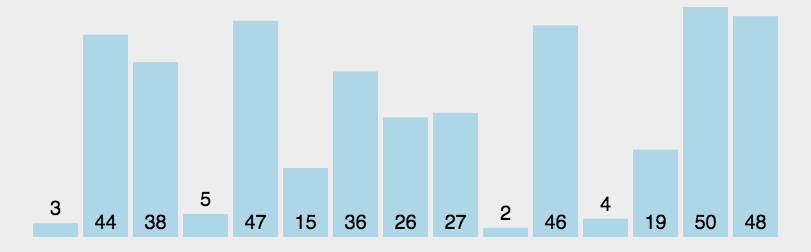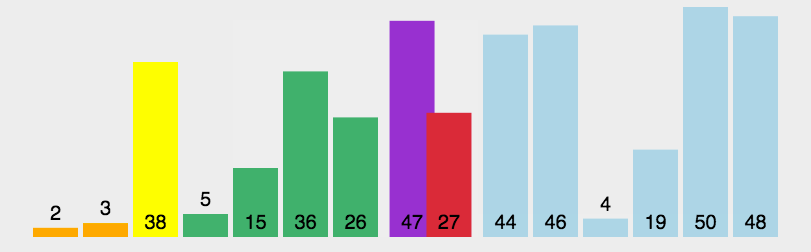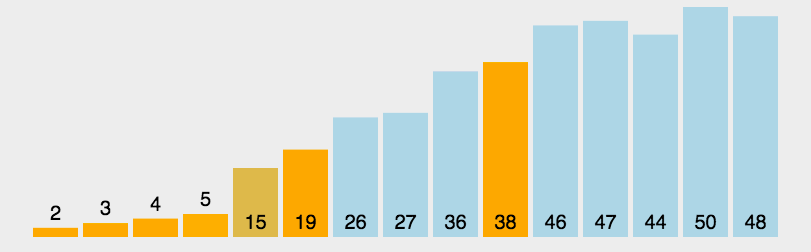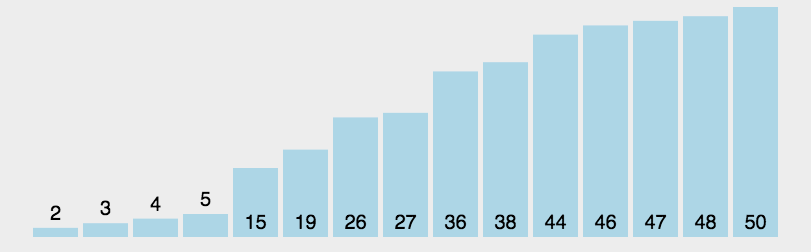
1 冒泡排序
这是一种简单的交换排序算法，通过比较两个元素的大小，确定是否交换顺序，通过遍历整个数列直到没有反序的记录为止。1.1 算法描述
- 比较相邻两个元素，确定是否交换
- 将数列中所有相邻元素进行比对，这样遍历一次后就能确定最后一个元素为最大值
- 重复以上步骤，但是每次都到上一次遍历的最后一个元素的前一个停止【前一次遍历排序了最大值】
1.2 时间复杂度
O(n^2)
1.3 代码实现
/*
* 算法导论 第二章 冒泡排序
* 思想：冒泡排序，顾名思义就是每一次将序列中最小的元素（较轻）移到前面去
* 轻的往上冒，重的往下掉，每次将未排序部分的最轻元素冒到最上面
* 时间复杂度为O(n^2)
*/
#include func bubbleSort(arr []int) []int{
len := len(arr);
for i := 0; i < len - 1; i++ {
for j := 0; j < len - 1 - i; j++ {
if(arr[j] > arr[j+1] { // 相邻元素两两对比
temp := arr[j+1] // 元素交换
arr[j+1] = arr[j]
arr[j] = temp
}
}
}
return arr;
}
2 快速排序
一种交换排序算法，【分治法，D&C = Divide and Conquer的应用】通过一趟排序将数列分成两个独立的部分，一部分记录关键字均比另一部分记录的关键字小，再分别对这两部分进行排序，直到整个序列有序。2.1 算法描述
- 选取基准值------作为将序列分割为两组元素的值
- 排序将大于基准值的交换至右侧，小于在左侧，与其相同的忽略
- 递归方法【Recursion】重复上述步骤将左右子序列排序
2.2 时间复杂度
平均O(nlogn)
递归调用，平均深度为O(logn)
说明：基准值的选取对于算法的复杂度影响较大，所以该算法是不稳定的算法。
由于实现方式使用递归，针对少量数据性能不佳，不如使用直接插入排序。
优化方案：1）low-high之间随机选取 2）三数取中：选取左右中三个值，取中间值 3）优化不必要的交换。
2.3 代码实现
int Partiton(int A[], int low, int high)
{
int i = low;
int x = A[low];//用子表的第一个记录作为枢纽值
//从左往右扫描,围绕x划分数组
for(int j = low+1 ; j <= high ; j++)
{
if(A[j] <= x)
{
i++;//i表示最后一个小于等于x的索引，最后要与A[low]交换，A[0]只作为temp临时值
if(i != j)
{
A[0] = A[i];
A[i] = A[j];
A[j] = A[0];
}
}
}
//A[low]填入i位置
A[0] = A[low];
A[low] = A[i];
A[i] = A[0];
return i;
}
void quicksort(int A[], int low, int high)
{
int w;
if(low < high)
{
w = Partiton(A, low, high);//把数组划分成两部分,w为计算出的枢纽值，且返回后数组元素A[w左边]比A[w]小，右边比A[w]大
quicksort(A, low, w-1);//对左半部分递归处理
quicksort(A, w+1, high);//对有半部分递归处理
}
}
void QuickSort(int L[]) {
QSort(L,1,sizeof(L)/sizeof(L[0]))
}
package main
import "fmt"
func quickSort(arr []int, start, end int) {
if start < end {
i, j := start, end
key := arr[(start+end)/2]
for i <= j {
for arr[i] < key {
i++
}
for arr[j] > key {
j--
}
if i <= j {
arr[i], arr[j] = arr[j], arr[i]
i++
j--
}
}
if start < j {
quickSort(arr, start, j)
}
if end > i {
quickSort(arr, i, end)
}
}
}
// 快速排序（直接）实现
func quickSort2(s []int) []int {
if len(s) < 2 {
return s
}
v := s[0]
var left, right []int
for _, e := range s[1:] {
if e <= v {
left = append(left, e)
} else {
right = append(right, e)
}
}
// 实现了“quickSort(left) + v + quickSort(right)”的操作
return append(append(quickSort(left), v), quickSort(right)...)
}
func main() {
arr := []int{3, 7, 9, 8, 38, 93, 12, 222, 45, 93, 23, 84, 65, 2}
quickSort(arr, 0, len(arr)-1)
fmt.Println(arr)
}
3 简单插入排序
基本思想：构建有序序列，将未排序的数据逐次插入有序序列中，使得新序列也有序。
3.1 算法描述
- 第一个元素默认有序
- 选下一个元素，将上述序列从后向前扫描，加入有序序列中
- 若元素值小于有序序列的元素，则向前继续扫描
- 不断重复上一步，直到找到有序序列中的位置【<=新元素】
- 将新元素插入该位置后面
- 重复2~5
3.2 时间复杂度
O(n^2)
3.3 代码实现
using namespace std;
void InsertSort(int a[], int size)
{
for (int i = 1; i < size; i++)
{
int index = i;
int key = a[index]; //待排序第一个元素
int end = index-1;//代表已经排过序的元素最后一个索引数
while (end >= 0 && key < a[end])//从后向前比对
{
a[end+1] = a[end];//将有序序列最后一个值右移一位，为新元素
end--;
}
a[end+1] = key;//在第一个小于key值的后面插入新元素
}
}
int main() {
int d[] = { 12, 15, 9, 20, 6, 31, 24 };
cout << "输入数组 { 12, 15, 9, 20, 6, 31, 24 } " << endl;
InsertSort(d,7);
cout << "排序后结果：";
for (int i = 0; i < 7; i++)
{
cout << d[i]<<" ";
}
return 0;
}
package main
import (
"fmt"
)
func InsertionSort(array [6]int, n int) {
var i, j int
var tmp int
for i = 1; i < n; i++ {
tmp = array[i]
for j = i; j > 0 && array[j-1] > tmp; j-- {
array[j] = array[j-1]
}
array[j] = tmp
}
fmt.Println(array)
}
func main() {
a := [...]int{34, 8, 64, 51, 32, 21}
fmt.Println(a)
num := len(a)
InsertionSort(a, num)
}
4 希尔排序
也是插入算法的一种，将整个集合根据不同的步长分成若干个子集和【相距某个“增量”的记录组成一个子序列】，子序列内进行直接插入排序-----基本有序。
4.1 算法描述
- 选择一个间隔【通常为长度的一半】，将整个集合进行分组；
- 在组内进行排序；
- 重新设置间隔【上次分组间隔的一半】，进行分组，并组内排序
- 直到分组间隔=1，最后进行排序
其中：
排序算法为插入排序算法
间隔既可以提前设定好间隔序列，也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法（第4版）》
4.2 时间复杂度
较好的增量序列可使时间复杂度降为：O(n^(3/2))，
甚至O(n^1.3) ,大量数据时，效率比插入排序高。
4.3 代码实现
#include func ShellSort(n []int,len int){
step := len/2
for ; step > 0;step=step/2 {
for i := step; i < len;i++ {
j := i-step
temp := n[i]
for j>=0 && temp < n[j] {
n[j+step] = n[j]
j=j-step
}
n[j+step] = temp
}
}
}
5 简单选择排序
选择排序的一种，从n-i+1中选出最小【大】的元素与第i个元素【进行n-i次比较】交换【1<=i<=n】。简单说就是：在未排序序列中找到最小（大）元素，存放至有序序列后，依次类推，不断取值，知道原序列为空，则新序列就是所有有序的元素。
5.1 算法描述
- 初始状态：无序区为R[1…n]，有序区为空；
- 第i趟排序(i=1,2,3…n-1)开始时，当前有序区和无序区分别为R[1…i-1]和R[i…n]。该趟排序从当前无序区中-选出最小【大】的元素;
- 将选出的元素R[x]与第i个元素交换，使得R[1…i]和R[i+1…n]分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；
- 进行 n-1趟结束，数组有序。
5.2 时间复杂度
虽然时间复杂度同为O(n^2),但是比较次数较多移动次数少，性能比冒泡要优一些。
稳定性较好，适合规模小的场景，且不需要额外空间。
5.3 代码实现
func SelectionSort(a []int, n int) {
if n <= 1 {
return
}
for i := 0; i < n; i++ {
// 查找最小值
minIndex := i
for j := i + 1; j < n; j++ {
if a[j] < a[minIndex] {
minIndex = j
}
}
// 交换
a[i], a[minIndex] = a[minIndex],a[i]
}
}
#include 6 堆排序
简单选择排序的改进，利用数据结构中“堆”的概念：具有某种性质的完全二叉树----每个节点的值>=左右孩子【大顶堆】，<=左右孩子【小顶堆】。
6.1 算法描述
1.将要排序的队列中构造成一个n个元素的大顶堆，那么根节点就是最大值；
2.排序，根节点与最后一个叶子节点交换，此时末尾元素就是最大值，并将剩余n-1的节点进行计算出一个次大顶堆；
3.以此类推。这样保证最后的元素都是排序好的，最终保证有序。
6.2 时间复杂度
O(nlogn)；构建堆排序次数较多,不适合个数较多的排序。
6.3 代码实现
//实现1
func buildMaxHeap(nums []int) { // 建立大顶堆
len := len(nums)
for i := len/2; i >= 0; i-- {//从最后一个父节点开始遍历，保证由底向上遍历后父节点都是最大的
heapify(nums, i)
}
}
func heapify(nums []int, parent int) { // 堆调整
len := len(nums)
left := 2 * parent + 1
right := 2 * parent + 2 //完全二叉树原理i节点的左右子节点索引为2i，2i+1【1开始计数】/2i+1,2i+2 【从0计数】
largest = parent
if left < len && nums[left] > nums[largest] {
largest = left;
}
if(right < len && nums[right] > nums[largest]) {
largest = right;
}
if(largest != parent) {//最大节点不是parent,则parent与child进行交换，反之认为
nums[parent], nums[largest] = nums[largest], nums[parent]
heapify(nums, largest);//递归遍历已经交换父节点后的子树重新调整保证大顶堆
}
}
func heapSort(arr []int) []int{
buildMaxHeap(arr);
len := len(arr)
for i := len - 1; i > 0; i-- {
arr[i], arr[0] = arr[0], arr[i]
len--
heapify(arr[0:len], 0);
}
return arr;
}
//实现2
func buildMaxHeap2(nums []int,parent,len int) { // 建立大顶堆
temp := nums[parent]
child := 2*parent+1//完全二叉树原理i节点的左右子节点索引为2i，2i+1【1开始计数】/2i+1,2i+2 【从0计数】
for child < len {
if child+1 < len && nums[child] < nums[child+1] {
child++//假如左节点小于右节点，则child选择右节点与parent比较
}
if child < len && nums[child] <= temp {
break//左右child节点都小于parent节点，则中断，本身parent已经是较大元素了，无需遍历所有子树【左右子节点都较小，比较也没有什么作用，且有整个buildMaxHeap的外循环】
}
nums[parent], nums[child]= nums[child], nums[parent]//parent 与child进行交换
parent = child//遍历该节点所有子树，使得子树也能满足堆的特征，且parent始终存放较大元素
child = child*2+1
}
nums[parent] = temp
}
func HeadSort(nums []int){
for i := len(nums)/2; i>=0; i-- {//完全二叉树原理，父节点索引i<=n/2向下取整
buildMaxHeap2(nums,i,len(nums))
}
for i := len(nums)-1;i >0; i--{
nums[0],nums[i] = nums[i],nums[0]//不断取根节点元素与最后节点进行交换
buildMaxHeap2(nums,0,i)//保证根节点nums[0]始终最大
}
}
#include7 归并排序（Merge Sort）
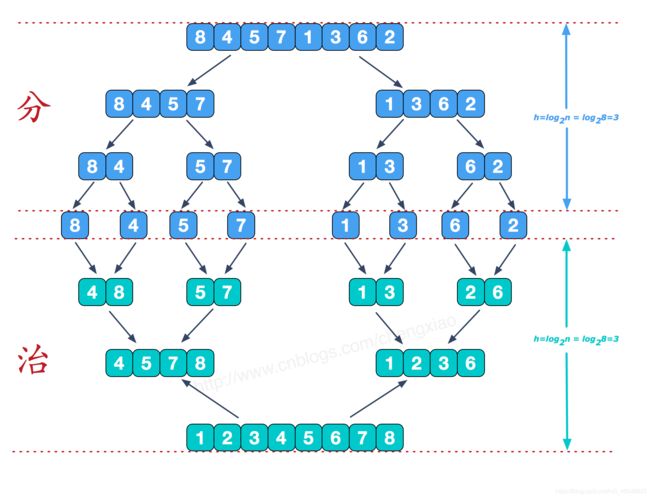
归并排序，又称二路/多路归并排序，是采用分治法（Divide & Conquer）的另一个典型【上一个为：快速排序】应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将n个有序表合并成一个有序表，称为n-路归并。 下面主要介绍二路归并。
注：分治法（D&C）：将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之。
基本思想如下：将待排序序列R[0…n-1]看成是n个长度为1的有序序列，将相邻的有序表成对归并，得到n/2个长度为2的有序表；将这些有序序列再次归并，得到n/4个长度为4的有序序列；如此反复进行下去，最后得到一个长度为n的有序序列
7.1 算法描述
- 把长度为n的输入序列分成两个长度为n/2的子序列；
- 对这两个子序列分别采用归并排序；
- 将两个排序好的子序列合并成一个最终的排序序列。
归并排序其实要做两件事：
（1）“分解”——将序列每次折半划分（递归实现）
（2）“合并”——将划分后的序列段两两合并后排序
- 在每次合并过程中，都是对两个有序的序列段进行合并，然后排序。 这两个有序序列段分别为 R[low, mid] 和 R[mid+1, high]。
- 先将他们合并到一个局部的暂存数组R2中，带合并完成后再将R2复制回R中。 我们称 R[low, mid] 第一段，R[mid+1, high] 为第二段。
- 每次从两个段中取出一个记录进行关键字的比较，将较小者放入R2中，最后将各段中余下的部分直接复制到R2中。
- 经过这样的过程，R2已经是一个有序的序列，再将其复制回R中，一次合并排序就完成了。
7.2 时间复杂度
O(nlogn),空间复杂度O(n+logn),比较占用内存但是效率高稳定。
当数据量较少时，QuickSort的运行时间比MergeSort的运行时间少；
随着数据增加，MergeSort的运行时间比QuickSort的运行时间少。
7.3 代码实现
实现：递归sort+merge
func MergeSort(n []int,start,end int){
if start >= end {
return
}
mid := (start+end)/2
MergeSort(n,start,mid)
MergeSort(n,mid+1,end)
Merge(n,start,mid,end)
}
func Merge(n []int,start,mid,end int){
var temp []int
i := start
k := mid + 1
j := 0
for ;i<=mid && k<=end;j++{
if n[i] < n[k] {
temp = append(temp,n[i])
i++
}else{
temp = append(temp,n[k])
k++
}
}
if i > mid {
temp=append(temp,n[k:end+1]...)
}else{
temp = append(temp,n[i:mid+1]...)
}
copy(n[start:end+1],temp)
}
/*
1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
4. 重复步骤3直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾
*/
#include 8 计数排序
非比较类排序，要求输入的数据必须有确定的范围的整数。
将输入数值转换为key值存放额外的数组中。
8.1 算法描述
- 找出排序序列的最大值和最小值
- 统计每个元素i出现的次数并记录于新数组c[i]中，并累加
- 反向填充目标数组：将每个元素i放在新数组第C[i]项，且每放一个，C[i]–
8.2 时间复杂度
当输入的元素是 n 个 0到 k 之间的整数时，时间复杂度是O(n+k)，但是需要额外的数组空间存放每个元素出现的次数，所以空间复杂度是O(n+k)，其排序速度快于任何比较排序算法。
适合于一定范围，K值不大且序列集中的情况。
8.3 代码实现
func CounterSort(arr []int, k int) {
len := len(arr)
c := make([]int, k+1)
sortindex := 0
for i := 0; i < len; i++ {
c[arr[i]]++
}
for j := 1; j < k+1; j++ {
for c[j]>0 {
a[sortindex] = j
sortindex++
c[j]--
}
}
return
}
void counting_sort(int A[], int n, int k)
{
int *c, *b;
int i;
c = (int *)malloc(sizeof(int)*k);/*临时数组,注意它的大小是待排序序列中值最大的那个。如假定该排序序列中最大值为1000000，则该数组需要1000000*sizeof(int)个存储单元*/
b = (int *)malloc(sizeof(int)*n); /*存放排序结果的数组*/
for (i = 0; i < k; i++)
c[i] = 0; /*初始化*/
for (i = 0; i < n; i++)
c[A[i]] += 1; /*统计数组A中每个值为i的元素出现的次数*/
for (i = 1; i < k; i++)
c[i] = c[i - 1] + c[i]; /*确定值为i的元素在数组c中出现的位置*/
for (i = n - 1; i >= 0; i--)
{
b[c[A[i]] - 1] = A[i]; /*对A数组，从后向前确定每个元素所在的最终位置;*/
c[A[i]] -= 1;
}
for (i = 0; i < n; i++)
A[i] = b[i];/*这个目的是返回A数组作为有序序列*/
free(c);
free(b);
}
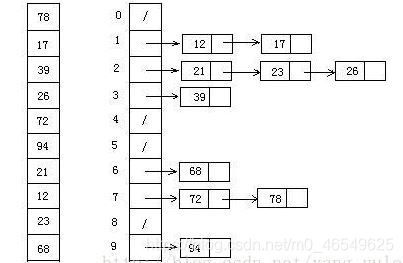
9 桶排序
计数排序的升级，利用函数映射关系。假如输入序列服从均匀分布，则将数据分到对应的桶中，分别排序（递归或其他排序算法）。
9.1 算法描述
- 设置有大小限制的空桶。
- 将序列分别以某种规则加入桶中
- 对非空桶进行排序
- 最后进行拼接
9.2 时间复杂度
对数组进行划分数据块，时间复杂度为O(n)，对每个数据块进行排序，时间复杂度取决于使用的排序算法。在极致情况下，每个桶只有一个数据，这样的时间复杂度无疑是最优的，因为每个数据块不需要进行排序。但是空间复杂度太高。
总之，桶排序的思想就是，将数组中的全部元素划分成若干个数据块，并对每个数据块分别进行排序，以此提高时间复杂度。该算法主要适合于数量比较大并且数字相对比较集中的场合。
9.3 算法实现
include <stdio.h>
#include package main
import (
"fmt"
"container/list"
)
func bucketSort(theArray []int,num int){
var theSort [99]int
for i:=0;i< len(theArray);i++{
theSort[10]=1
if theSort[theArray[i]] !=0{
theSort[theArray[i]] = theSort[theArray[i]]+1
}else{
theSort[theArray[i]] = 1
}
}
l:=list.New()
for j:=0;j<len(theSort);j++{
if theSort[j]==0{
//panic("error test.....")
}else{
for k:=0;k<theSort[j];k++{
l.PushBack(j)
}
}
}
for e := l.Front(); e != nil; e = e.Next() {
fmt.Print(e.Value, " ")
}
}
func main() {
var theArray = []int{10, 1, 18, 30, 23, 12, 7, 5, 18, 17}
fmt.Print("排序前")
fmt.Println(theArray)
fmt.Print("排序后")
bucketSort(theArray,11)
}
10 基数排序
基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。
10.1 算法描述
- 取得数组中的最大数，并取得位数；
- arr为原始数组，从最低位开始取每个位组成新数组；
- 对新数组进行计数排序（利用计数排序适用于小范围数的特点）；
10.2 时间复杂度
基数排序基于分别排序，分别收集，所以是稳定的。但基数排序的性能比桶排序要略差，每一次关键字的桶分配都需要O(n)的时间复杂度，而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字，则基数排序的时间复杂度将是O(d*2n) ，当然d要远远小于n，因此基本上还是线性级别的。
基数排序的空间复杂度为O(n+k)，其中k为桶的数量。一般来说n>>k，因此额外空间需要大概n个左右。
10.3 代码实现
#include package main
import (
"algorithms"
"fmt"
)
func main() {
arr := algorithms.GetArr(5, 1000)
//arr = []int{27, 38, 12, 101, 27, 16}
fmt.Println("[UNSORTED]:\t", arr)
fmt.Println("[SORTED]:\t", radixSort(arr))
}
func radixSort(arr []int) []int {
max := getMax(arr)
// 数组中最大值决定了循环次数，101 循环三次
for bit := 1; max/bit > 0; bit *= 10 {
arr = bitSort(arr, bit)
fmt.Println("[DEBUG bit]\t", bit)
fmt.Println("[DEBUG arr]\t", arr)
}
return arr
}
//
// 对指定的位进行排序
// bit 可取 1，10，100 等值
//
func bitSort(arr []int, bit int) []int {
n := len(arr)
// 各个位的相同的数统计到 bitCounts[] 中
bitCounts := make([]int, 10)
for i := 0; i < n; i++ {
num := (arr[i] / bit) % 10
bitCounts[num]++
}
for i := 1; i < 10; i++ {
bitCounts[i] += bitCounts[i-1]
}
tmp := make([]int, 10)
for i := n - 1; i >= 0; i-- {
num := (arr[i] / bit) % 10
tmp[bitCounts[num]-1] = arr[i]
bitCounts[num]--
}
for i := 0; i < n; i++ {
arr[i] = tmp[i]
}
return arr
}
// 获取数组中最大的值
func getMax(arr []int) (max int) {
max = arr[0]
for _, v := range arr {
if max < v {
max = v
}
}
return
}
11 算法比较
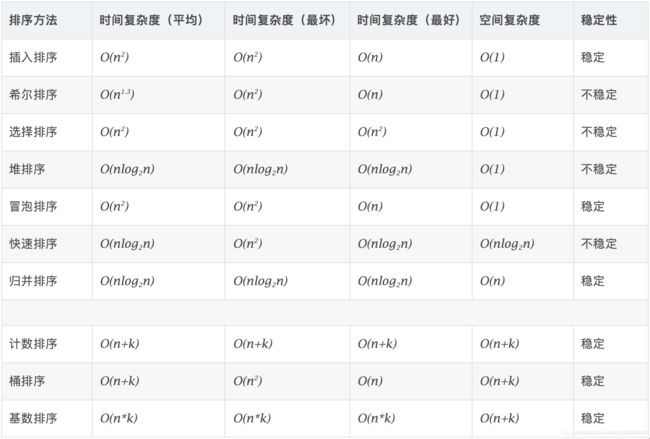
其中
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。
在云计算之类的环境中，待排序的数据是实时生成的，在排序算法开始运行时，数据并未完全就绪，而是随着排序算法本身的进行而逐步给出的。当然也要考虑算法的并行性和串行性。
更多：https://blog.csdn.net/zhangjikuan/article/details/49095533