实验4:最优化模型实验
实验4:最优化模型实验
4.1 基础训练
- 求函数极值
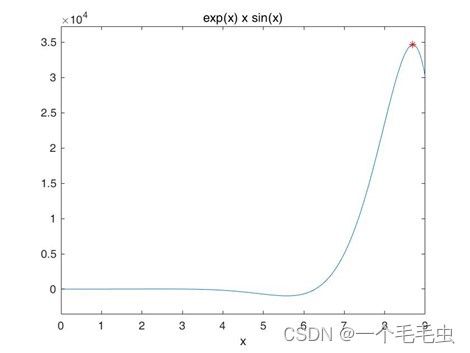
求一元函数 f ( x ) = e x s i n x f(x)=e^xsinx f(x)=exsinx在区间[0,9]内的最大值点、最大值,并绘制出函数图形,编写function程序文件返回2个参数,依次返回最大值点、最大值.
提示:调用函数fminbnd计算;先绘制函数曲线,通过观察确定最大值点所在区间.
参考函数如下:
function [x0,y0]=fun
代码:
function [x0,y0] = fun
%定义并画出原函数
fun1 = inline('exp(x)*x*sin(x)');
ezplot(fun1,[0,9]),hold on
%根据图像判断最大值在8到9之间
fun2 = inline('exp(x)*(-x)*sin(x)');
[x0,y0] = fminbnd(fun2,8,9);
%计算真实最大值
y0 = -y0;
plot(x0,y0,'r*')
end
- 求解下列线性规划模型
m a x f ( x 1 , x 2 , x 3 ) = 2.5 x 1 + 5 x 2 + 10 x 3 max f(x_1,x_2,x_3)=2.5x_1+5x_2+10x_3 maxf(x1,x2,x3)=2.5x1+5x2+10x3
s . t . { x 1 + x 2 + x 3 = 100 2.5 x 1 + 5 x 2 + 10 x 3 ≥ 50 x 3 ≤ 2 ( x 1 + x 2 ) 10 ≤ x 1 ≤ 30 0 ≤ x 2 ≤ 90 20 ≤ x 3 ≤ 80 s.t. \begin{cases}x_1+x_2+x_3=100\\2.5x_1+5x_2+10x_3\ge 50\\x_3\le2(x_1+x_2)\\10\le x_1\le 30\\0\le x_2\le 90\\20\le x_3\le 80 \end{cases} s.t.⎩ ⎨ ⎧x1+x2+x3=1002.5x1+5x2+10x3≥50x3≤2(x1+x2)10≤x1≤300≤x2≤9020≤x3≤80
提示:先把本模型化为MATLAB求解的线性规划模型的一般形式.如目标函数改为极小化,还有约束条件的转换.
解:
化为一般形式如下:
m i n g ( x 1 , x 2 , x 3 ) = − 2.5 x 1 − 5 x 2 − 10 x 3 min\quad g(x_1,x_2,x_3)=-2.5x_1-5x_2-10x_3 ming(x1,x2,x3)=−2.5x1−5x2−10x3
s . t . { x 1 + x 2 + x 3 = 100 − 2.5 x 1 − 5 x 2 − 10 x 3 ≤ − 50 − 2 x 1 − 2 x 2 + x 3 ≤ 0 10 ≤ x 1 ≤ 30 0 ≤ x 2 ≤ 90 20 ≤ x 3 ≤ 80 s.t. \begin{cases}x_1+x_2+x_3=100\\-2.5x_1-5x_2-10x_3\le -50\\-2x_1-2x_2+x_3\le0\\10\le x_1\le 30\\0\le x_2\le 90\\20\le x_3\le 80 \end{cases} s.t.⎩ ⎨ ⎧x1+x2+x3=100−2.5x1−5x2−10x3≤−50−2x1−2x2+x3≤010≤x1≤300≤x2≤9020≤x3≤80
代码:
Aeq = [1,1,1]; %等式线性约束矩阵和向量
beq = [100];
A = [-2.5 -5 -10;-2 -2 1]; %不等式线性约束矩阵和向量
b = [-50;0];
Lb = [10,0,20]; %边界约束向量
Ub = [30,90,80];
[x,fval] = linprog(C,A,b,Aeq,beq,Lb,Ub)
运行结果:
由结果可知,最大值约为808.333
- 通过对某实际问题建模得到下列最优化模型,请完成如下实验任务.
m i n f ( x ) = 2 ( x 1 − 1 ) 2 + 3 ( x 2 − 1 ) 2 + 0.2 x 1 x 2 + 0.2 x 2 x 3 + ( 2 x 3 − 2 ) 2 min\quad f(x)=2(x_1-1)^2+3(x_2-1)^2+0.2x_1x_2+0.2x_2x_3+(2x_3-2)^2 minf(x)=2(x1−1)2+3(x2−1)2+0.2x1x2+0.2x2x3+(2x3−2)2
s . t . { 3 x 1 + 2 x 2 + 6 x 3 ≤ 50 , 4 x 1 + 5 x 2 + 2 x 3 ≤ 40 2 x 1 + 9 x 2 + 7 x 3 ≤ 100 2 x 1 2 + x 2 2 + x 3 2 ≥ 5 x 1 2 + x 2 2 + 2 x 3 2 ≤ 200 0 ≤ x 1 ≤ 15 0 ≤ x 2 ≤ 9 0 ≤ x 3 ≤ 25 且 x 3 为整数 s.t.\begin{cases}3_x1+2_x2+6x_3\le50,\\4x_1+5x_2+2x_3\le 40\\2x_1+9x_2+7x_3\le 100\\2x_1^2+x_2^2+x_3^2\ge5\\x_1^2+x_2^2+2x_3^2\le200\\0\le x_1\le 15\\0\le x_2\le 9\\0\le x_3\le 25且x_3为整数\end{cases} s.t.⎩ ⎨ ⎧3x1+2x2+6x3≤50,4x1+5x2+2x3≤402x1+9x2+7x3≤1002x12+x22+x32≥5x12+x22+2x32≤2000≤x1≤150≤x2≤90≤x3≤25且x3为整数
(1)利用MATLAB最优化工具箱函数fmincon的用法,调用fmincon函数求解上述模型.
(2)请学习MATLAB遗传算法工具箱函数ga的用法,调用ga函数求解上述模型.
提示: 根据优化函数求出最优解后,可将 x 3 x_3 x3取整,然后确定其取值.
(1) 代码:
%主函数
function testmain1
A = [3 2 6;4 5 2;2 9 7];
b = [50;40;100];
Aeq = [];
beq = [];
Lb = [0;0;0];
Ub = [15;9;25];
x0 = [0;0;0];
[xmin,fmin] = fmincon(@fun,x0,A,b,Aeq,beq,Lb,Ub,@nonlcon)
end
%目标函数
function f =fun(x)
f = 2*(x(1)-1)^2+3*(x(2)-1)^2+0.2*x(1)*x(2)+0.2*x(2)*x(3)+(2*x(3)-2)^2;
end
%定义非线性约束子函数
function [c,ceq] = nonlcon(x)
c = [-2*x(1)^2-x(2)^2-x(3)^2+5;x(1)^2+x(2)^2+2*x(3)^2-200];
ceq = [];
end
运行结果:
将 x 3 x_3 x3取整为1
(2)代码:
%主函数
function testmain1
A = [3 2 6;4 5 2;2 9 7];
b = [50;40;100];
Aeq = [];
beq = [];
Lb = [0;0;0];
Ub = [15;9;25];
n = 3;
[xmin,fmin] = ga(@fun,n,A,b,Aeq,beq,Lb,Ub,@nonlcon)
end
%目标函数
function f =fun(x)
f = 2*(x(1)-1)^2+3*(x(2)-1)^2+0.2*x(1)*x(2)+0.2*x(2)*x(3)+(2*x(3)-2)^2;
end
%定义非线性约束子函数
function [c,ceq] = nonlcon(x)
c = [-2*x(1)^2-x(2)^2-x(3)^2+5;x(1)^2+x(2)^2+2*x(3)^2-200];
ceq = [];
end
运行结果:
观察可得,运行3次后,结果与fmincon基本一致。
4.2 综合训练
一、实验任务
某工厂有三种原料C1,C2,C3,其储量分别为150公斤,160公斤和180公斤。现在用来生产甲、乙两种产品。已知每生产1公斤产品甲需要原料C1 3公斤,原料C2 6公斤,原料C3 2公斤。每生产1公斤产品乙需要原料C1 5公斤,原料C2 5公斤,原料C3 6公斤。又已知生产1公斤产品甲利润为17元,生产1公斤产品乙利润为15元。请为该工厂制定生产计划,使得利润尽可能大.
二、实验目的
认识线性规划模型。
熟悉Matlab求解线性规划模型的函数linprog。
三、实验过程(需要写出建立的数学模型、程序代码和计算结果)
(一)建立数学模型:
设生产产品甲数量 x 1 x_1 x1公斤,产品乙数量 x 2 x_2 x2公斤,则目标函数为
m a x f ( x 1 , x 2 ) = 17 x 1 + 15 x 2 max\quad f(x_1,x_2)=17x_1+15x_2 maxf(x1,x2)=17x1+15x2
约束条件为:
{ 3 x 1 + 5 x 2 ≤ 150 6 x 1 + 5 x 2 ≤ 160 2 x 1 + 6 x 2 ≤ 180 x 1 ≥ 0 x 2 ≥ 0 \begin{cases}3x_1+5x_2\le150\\6x_1+5x_2\le 160\\2x_1+6x_2\le 180\\x_1\qquad\quad \ge 0\\ \qquad\quad x_2\ge 0\end{cases} ⎩ ⎨ ⎧3x1+5x2≤1506x1+5x2≤1602x1+6x2≤180x1≥0x2≥0
化为标准形式:
m i n g ( x 1 , x 2 ) = − 17 x 1 − 15 x 2 min\quad g(x_1,x_2)=-17x_1-15x_2 ming(x1,x2)=−17x1−15x2
{ 3 x 1 + 5 x 2 ≤ 150 6 x 1 + 5 x 2 ≤ 160 2 x 1 + 6 x 2 ≤ 180 − x 1 ≤ 0 − x 2 ≤ 0 \begin{cases}3x_1+5x_2\le 150\\6x_1+5x_2\le160\\2x_1+6x_2\le180\\-x_1 \qquad \le 0\\ \qquad -x_2\le 0\end{cases} ⎩ ⎨ ⎧3x1+5x2≤1506x1+5x2≤1602x1+6x2≤180−x1≤0−x2≤0
(二)程序代码:
C = [-17,-15];
A = [3 5;6 5;2 6;-1 0;0 -1];
b = [150;160;180;0;0];
Aeq = [];
beq = [];
Lb = [0;0];
Ub =[inf;inf];
[x,fval] = linprog(C,A,b,Aeq,beq,Lb,Ub)
(三)计算结果:
由运行结果可知,生产产品甲3.333公斤,产品乙28.0000公斤时,利润有最大值476.6667元。
四. 实验自评与改进x_1方向
(一)实验自评:
内容上:较好地完成了实验任务,达成实验目标,获得了正确的预期实验结果;
形式上:排版较为清晰明了,代码用黑底彩色标注便于识别,报告整体清晰美观。
(二)改进方向:
应该进一步加深对MATLAB最优化工具箱函数的熟悉程度,达到不用翻看课本和课件也能熟练运用的效果。
五. 实验体会,收获及建议
通过本次实验,我认识到了最优化问题在生活中的普遍性,以及解决最优化问题的必要性。MATLAB在求解最优化问题时,通过调用自带的最优化工具箱函数便可以高效率地解决绝大部分的最优化问题,与其他方法相比具有很大的优势。在实验过程中,我收获良多,不仅进一步熟悉了常用的最优化函数,而且从实际问题中抽象数学模型的能力也得到很大提升,对以后的学习科研具有很大的帮助。