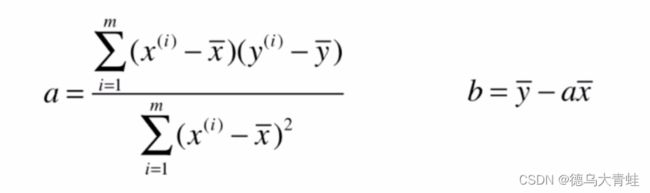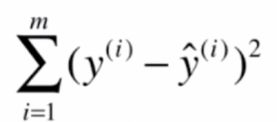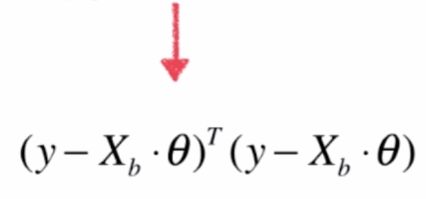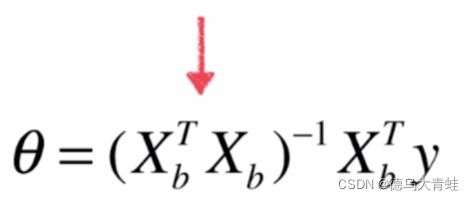线性回归算法原理及python实现

引言

回归与分类的区别

区分回归与分类其实很简单，举个例子，预测病人患病概率，结果只有患病和不患病2种，这就是分类；预测房价，结果可能是在一段区间内，这个就是回归。

线性回归

线性回归是利用数理统计中回归分析方法，其本质是寻找出一条线最大程度的拟合特征及样本输出间的关系。

线性回归具有以下特点

1. 思想简单，容易实现
2. 是其他许多非线性回归模型的基础
3. 结果具有很好的可解释性

简单线性回归

原理及推导

当样本只有一个特征时，称为简单线性回归。例如房屋价格和房屋面积之间的关系。

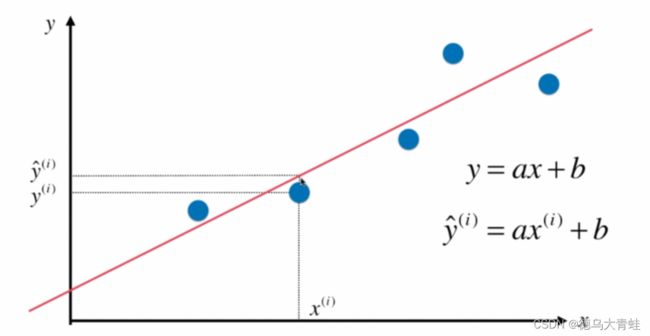
假设我们找到了最佳的拟合直线方程为y=ax+b,则对于每个样本点预测值为

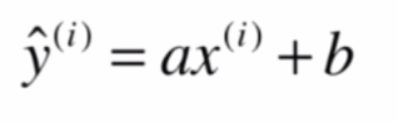
实际值为

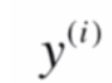
要使得预测结果最贴近实际值，那么预测值减去实际值的值要最小，一般用样本点预测值减实际值的平方和表示，也称之为损失函数，我们要做的就是求得a,b使损失函数值尽可能小。


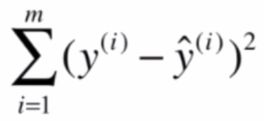
根据大学的高数可知求得a,b使损失函数值尽可能小，即对损失函数分别对a，b求导，使得求导结果等于0处即是极值，求导的结果得：

python实现算法

样本数据

import numpy as np
import matplotlib.pyplot as plt
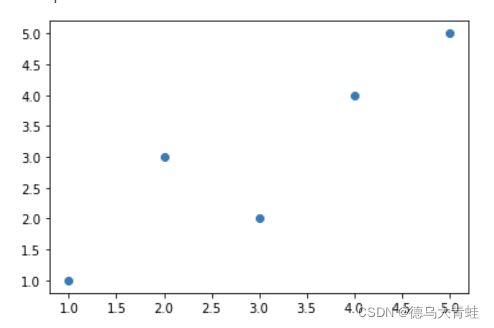
x_data = np.array([1,2,3,4,5])
y_data = np.array([1,3,2,4,5])
plt.scatter(x_data,y_data)
plt.show()

算法实现

sub1 = 0.0
sub2 = 0.0
for x_i,y_i in zip(x_data,y_data):
    sub1 += (x_i-np.mean(x_data))*(y_i-np.mean(y_data))
    sub2 += (x_i-np.mean(x_data))**2
a = sub1/sub2
b = np.mean(y_data)-a*np.mean(x_data)

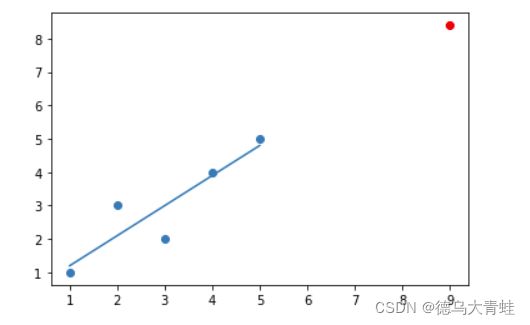
x_predict = 9
y_predict = a * x_predict + b

多元线性回归

原理及推导

当x为1个向量时，此时就是多元线性回归。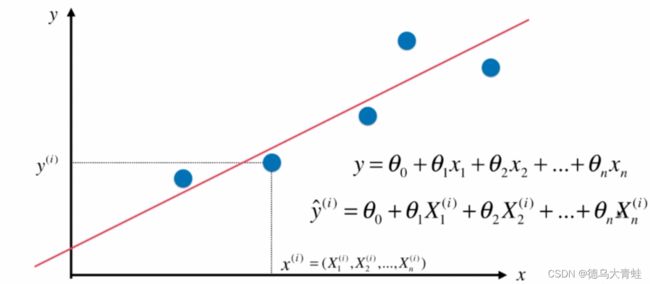
多元线性回归一个观测值就不再是一个标量而是一个向量了，而对应的因变量的观测值不变，因此我们把这些观测值每一行每一行的叠加起来就成为了一个向量或者矩阵。

此时损失函数为

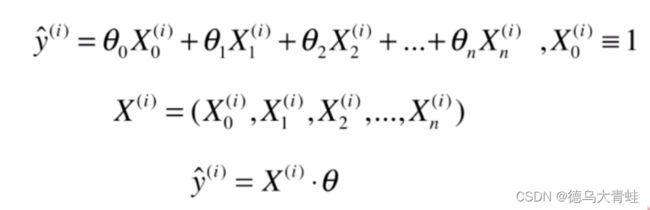
python实现算法

手工实现多元线性回归算法

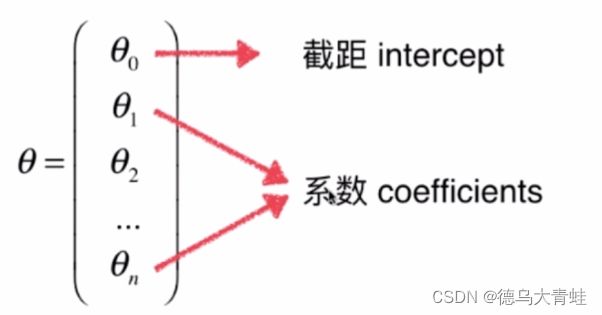
线性回归方程可以分为系数和截距2部分，例如y=a*x+b，a为系数，b为截距，同理可得出多元线性回归方程的系数和截距如下：

import numpy as np
class LinearRegression:
    def __init__(self):
        self.intercept = None
        self.coef = None

    def fit(self,x_train,y_train):
        #x_b为x_train前加一列1
        x_b = np.hstack((np.ones((len(x_train),1)),x_train))
        #根据上节theta公式求theta
        self._theta = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y_train)
        self.intercept = self._theta[0]
        self.coef = self._theta[1:]
        return self

    def predict(self,x_test):
        x_b = np.hstack((np.ones((len(x_test),1)),x_test))
        y_predict = x_b.dot(self._theta)
        return y_predict

    #计算R 方差
    def score(self,x_test,y_test):
        y_predict = self.predict(x_test)
        mean_squared_error = np.sum((y_test - y_predict)**2) / len(y_test)
        r2_score = 1 - mean_squared_error/np.var(y_test)
        return r2_score

sklearn实现多元线性回归算法

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston

boston = load_boston()
x_data = boston.data
y_data = boston.target
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.2)

LinearRegression = LinearRegression()
LinearRegression.fit(x_train, y_train)

y_predict = LinearRegression.predict(x_test)
score = LinearRegression.score(x_test, y_test)