牛客周赛 Round 23
A.小红的整数转换
题目描述
小红拿到了两个正整数x和y,她希望构造两个正整数a和b,满足以下性质:
对x执行a次以下操作:使x加上b。操作结束后使得x等于y。
请你构造任意合法解。共有t组询问。
输入描述:
第一行输入一个正整数t,代表询问的次数。
接下来的t行,每行输入两个正整数x和y,代表一次询问。
1≤t,x,y≤100
输出描述:
对于每次询问,如果无解,则输出两个-1。
否则输出两个正整数,代表一个合法解。
有多解时输出任意即可。
示例1
输入
2 1 5 2 2
输出
2 2 -1 -1
说明
第一组询问,对1进行两次加2操作,即可使其变成5。
第二组询问,显然没有任何合法操作。
解题思路:
由于a,b都是正整数,那么只要x>=y,就无法构造,只要x 可以让a=1,b=y-x就是一组答案 综上所述当x>=y时,无法构造,输出-1,-1 x cpp代码如下 小红想让你打印一个大小为 n 的 'O'字母。你能帮帮她吗? 没什么好说的,直接根据题意模拟就行了 cpp代码如下 小红想构造一个总共 n 个节点完全二叉树,该二叉树满足以下两个性质: 首先我们拿到的点从1开始的连续的点,也就是[1,2,3,...,n],从1开始也就是奇数开始。 (1)如果n是奇数那么奇数结尾,奇数的个数就比偶数的个数多1。 (2)如果n是偶数那么偶数结尾,奇数的个数和偶数的个数是一样的。 也就是说奇数的个数要么比偶数的个数多1,要么和偶数的个数相同 然后就可以考虑构造了,题目要求构造一棵完全二叉树,首先完全二叉树就是上面的所有层都必须是满的,最后一层可以满也可以不满,当最后一层也满时完全二叉树就变为了满二叉树,满二叉树就是所有层都是满的的二叉树。 对于一颗满二叉树,最后一层结点个数是上面所有的层的结点个数之和+1,根据这个性质就可以发现存在一个很容易的构造方式了,先把偶数点放在上面,奇数点全部作为叶子结点挂在下面。 此时我们就可以考虑到一种可能的构造方式就是偶数点全放在上面的所有层,奇数点全部放在叶子结点,那么这种构造一定符合要求吗,答案是符合的,下面来证明一下,我们可以知道的是把所有的偶数点放在上面构造出来的一定是一颗满二叉树或者完全二叉树。 (1)当把所有偶数点放完之后是一颗满二叉树,如下图所示 根据满二叉树的性质最后一层可以放上面所有层点结点个数加1个结点,所以只要奇数点的个数小于等于偶数点的个数加1就可以把所有奇数点放在叶子结点,上面已经分析出了奇数的个数要么和偶数点的个数相同,要么比偶数点的个数多1,刚好是满足这个要求的,至此满足所有结点和父结点的权值乘积都为偶数,所以是一种符合要求的构造。 (2)当把所有偶数点放在上面的所有层是一颗完全二叉树,但不是满二叉树,如下图所示 此时我们需要考虑的就是能否把所有奇数点都挂在叶子结点下面作为新的叶子结点 这个完全二叉树最后一层如果是满的,那么假设满的时候有x个结点,假设此时的完全二叉树有y个结点,也就是说少了x-y个结点,我们可以发现最后一层本来每一个结点下面可以挂俩个叶子,如果某个叶子缺失了,那么就只能将叶子挂到上一层去,到了上一层这个位置就只能挂一个叶子了, 那么此时可以挂在叶子的奇数点的结点个数就是y*2+x-y=x+y,我们需要计算一下此时的奇数结点个数是多少个,首先最后一层满的时候有x个结点,那么上面所有层的结点个数就是x-1,加上当前层的y个结点,那么就有x-1+y偶数结点,由于奇数结点个数<=偶数结点个数+1,也就是说奇数结点个数<=x-1+y+1=x+y,上面分析出了可以挂在叶子上面的奇数结点个数最多刚好为x+y,所以所有的奇数结点是都可以挂在最下面的叶子结点下面作为新的叶子结点的。 到此就证明完了,说明上述构造方式是合法的 cpp代码如下 小红有n个硬币,其中一些硬币为红色,另外一些为蓝色。每个硬币有一个面值(保证所有硬币的面值不同)。 小红想选择一些硬币凑出总面值为p,且至少有一个红硬币和至少一个蓝硬币,你能她求出选择的方案数吗?答案对1e9+7取模。 提示:建议python考生使用pypy提交。 要凑出总面值为m,并且至少有一个红硬币和至少有一个蓝硬币,如果直接分类讨论可以发现情况非常多,不好计算,这就该用到常用的技巧正难则反了,上面的情况就可以转换为总方案-只有红色硬币的方案数-只有蓝色硬币的方案数。 对于这三种情况考虑dp (1)要凑出面值为m,且所有硬币都可以使用的方案数 定义f[i]表示凑出面值为i的硬币的方案数 初始值f[0]=1,(凑出面值为0的方案数为1个,就是什么也不选) 状态转移 答案就是f[m],记tot1=f[m] (2)要凑出面值为m,且只使用红色硬币的方案数 定义f[i]表示凑出面值为i的硬币的方案数 初始值f[0]=1,(凑出面值为0的方案数为1个,就是什么也不选) 状态转移 答案就是f[m],记f[m]=tot2 (3)要凑出面值为m,且只使用蓝色硬币的方案数 定义f[i]表示凑出面值为i的硬币的方案数 初始值f[0]=1,(凑出面值为0的方案数为1个,就是什么也不选) 状态转移 最终答案就是tot1-tot2-tot3 cpp代码如下#include B.小红打O
题目描述
'O'字母的打印细节请参考样例。输入描述:
一个正整数 n,代表打印的图形大小。
1≤n≤50
输出描述:
一共 4n 行,每行输出一个长度为 4n 的字符串。
示例1
输入
1
输出
.**.
*..*
*..*
.**.
示例2
输入
2
输出
..****..
.******.
**....**
**....**
**....**
**....**
.******.
..****..
示例3
输入
3
输出
...******...
..********..
.**********.
***......***
***......***
***......***
***......***
***......***
***......***
.**********.
..********..
...******...
解题思路:
#include C.小红的完全二叉树构造
题目描述
1. 所有节点的权值值为 1 ~ n 的一个排列。
2. 除了根节点以外,每个节点的权值和它父亲的权值的乘积为偶数。
请你帮小红构造出这个二叉树,并按层序遍历的方式打印所有节点。输入描述:
一个正整数 n,代表二叉树的节点数量。
2≤n≤1e5
输出描述:
输出一行n个正整数,代表小红构造的二叉树的层序遍历的序列。
示例1
输入
4
输出
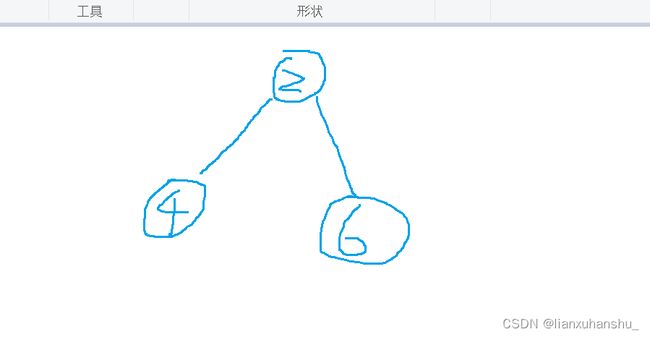
2 4 3 1
说明
解题思路:
#include D.小红的红蓝硬币
题目描述
输入描述:
第一行输入两个正整数n和p,用空格隔开。
第二行输入一个仅包含'R'和'B'的字符串,第i个字符为'R'代表第i个硬币为红色,'B'代表蓝色。
第三行输入n个正整数ai,代表每个硬币的面值。
1≤n,ai≤1000
1≤p≤10000
输出描述:
一个正整数,代表方案数对1e9+7取模的值。
示例1
输入
5 10
BBRRR
1 2 3 6 8
输出
2
说明
1(蓝色)+3(红色)+6(红色)
2(蓝色)+8(红色)
示例2
输入
5 10
RRRRR
1 2 3 6 8
输出
0
说明
所有硬币都是红色,因此没有合法的方案。
解题思路:
for(int i=1;i<=n;i++)
{
for(int j=m;j>=a[i];j--)
{
f[j]+=f[j-a[i]];
f[j]%=mod;
}
}for(int i=1;i<=n;i++)
{
for(int j=m;j>=a[i];j--)
{
if(s[i]=='R')f[j]+=f[j-a[i]];
f[j]%=mod;
}
} for(int i=1;i<=n;i++)
{
for(int j=m;j>=a[i];j--)
{
if(s[i]=='B')f[j]+=f[j-a[i]];
f[j]%=mod;
}
}#include