海量数据处理算法—Bit-Map

1. Bit Map算法简介        来自于《编程珠玑》。所谓的Bit-map就是用一个bit位来标记某个元素对应的Value， 而Key即是该元素。由于采用了Bit为单位来存储数据，因此在存储空间方面，可以大大节省。

 

 

2、 Bit Map的基本思想

        我们先来看一个具体的例子，假设我们要对0-7内的5个元素(4,7,2,5,3)排序（这里假设这些元素没有重复）。那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数，我们就只需要8个Bit（1Bytes），首先我们开辟1Byte的空间，将这些空间的所有Bit位都置为0，如下图：
                                                      

然后遍历这5个元素，首先第一个元素是4，那么就把4对应的位置为1（可以这样操作 p+(i/8)|(0x01<<(i%8)) 当然了这里的操作涉及到Big-ending和Little-ending的情况，这里默认为Big-ending）,因为是从零开始的，所以要把第五位置为一（如下图）：

                                                     

然后再处理第二个元素7，将第八位置为1,，接着再处理第三个元素，一直到最后处理完所有的元素，将相应的位置为1，这时候的内存的Bit位的状态如下：

                                                   

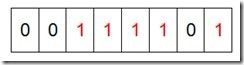
然后我们现在遍历一遍Bit区域，将该位是一的位的编号输出（2，3，4，5，7），这样就达到了排序的目的。

 

优点：

1.运算效率高，不许进行比较和移位；

2.占用内存少，比如N=10000000；只需占用内存为N/8=1250000Byte=1.25M。 缺点：

       所有的数据不能重复。即不可对重复的数据进行排序和查找。   

 

算法思想比较简单，但关键是如何确定十进制的数映射到二进制bit位的map图。

 

 

3、 Map映射表

假设需要排序或者查找的总数N=10000000，那么我们需要申请内存空间的大小为int a[1 + N/32]，其中：a[0]在内存中占32为可以对应十进制数0-31，依次类推： bitmap表为： a[0]--------->0-31 a[1]--------->32-63 a[2]--------->64-95 a[3]--------->96-127 .......... 那么十进制数如何转换为对应的bit位，下面介绍用位移将十进制数转换为对应的bit位。

 

 

3、 位移转换

 

 

申请一个int一维数组，那么可以当作为列为32位的二维数组，

               |                           32位                                       |

int a[0]    |0000000000000000000000000000000000000|

int a[1]    |0000000000000000000000000000000000000|

………………

int a[N]   |0000000000000000000000000000000000000|

例如十进制0，对应在a[0]所占的bit为中的第一位： 00000000000000000000000000000001 0-31：对应在a[0]中 i =0                            00000000000000000000000000000000 temp=0                     00000000000000000000000000000000 answer=1                 00000000000000000000000000000001

i =1                            00000000000000000000000000000001 temp=1                     00000000000000000000000000000001 answer=2                 00000000000000000000000000000010

i =2                            00000000000000000000000000000010 temp=2                     00000000000000000000000000000010 answer=4                 00000000000000000000000000000100

i =30                              00000000000000000000000000011110 temp=30                       00000000000000000000000000011110

answer=1073741824  01000000000000000000000000000000

i =31                               00000000000000000000000000011111 temp=31                         00000000000000000000000000011111 answer=-2147483648 10000000000000000000000000000000
32-63：对应在a[1]中 i =32                            00000000000000000000000000100000 temp=0                        00000000000000000000000000000000 answer=1                    00000000000000000000000000000001

i =33                            00000000000000000000000000100001 temp=1                       00000000000000000000000000000001 answer=2                    00000000000000000000000000000010

i =34                            00000000000000000000000000100010 temp=2                        00000000000000000000000000000010 answer=4                    00000000000000000000000000000100

i =61                              00000000000000000000000000111101 temp=29                       00000000000000000000000000011101 answer=536870912    00100000000000000000000000000000

i =62                               00000000000000000000000000111110 temp=30                        00000000000000000000000000011110 answer=1073741824  01000000000000000000000000000000

i =63                                00000000000000000000000000111111 temp=31                         00000000000000000000000000011111 answer=-2147483648  10000000000000000000000000000000
浅析上面的对应表，分三步： 1.求十进制0-N对应在数组a中的下标： 十进制0-31，对应在a[0]中，先由十进制数n转换为与32的余可转化为对应在数组a中的下标。比如n=24,那么 n/32=0，则24对应在数组a中的下标为0。又比如n=60,那么n/32=1，则60对应在数组a中的下标为1，同理可以计算0-N在数组a中的下标。

2.求0-N对应0-31中的数：

十进制0-31就对应0-31，而32-63则对应也是0-31，即给定一个数n可以通过模32求得对应0-31中的数。

3.利用移位0-31使得对应32bit位为1.

找到对应0-31的数为M, 左移M位：即2^M. 然后置1.

 

由此我们计算10000000个bit占用的空间：

1byte = 8bit

1kb = 1024byte

1mb = 1024kb

占用的空间为：10000000/8/1024/1024mb。

大概为1mb多一些。

 

 

3、 扩展

        Bloom filter可以看做是对bit-map的扩展

 

4、 Bit-Map的应用

      1）可进行数据的快速查找，判重，删除，一般来说数据范围是int的10倍以下。

       2）去重数据而达到压缩数据

 

5、 Bit-Map的具体实现

c语言实现：

 

#define BITSPERWORD 32
#define SHIFT 5
#define MASK 0x1F
#define N 10000000

int a[1 + N/BITSPERWORD];//申请内存的大小


//set 设置所在的bit位为1
void set(int i) {
    a[i>>SHIFT] |=  (1<<(i & MASK));
}
//clr 初始化所有的bit位为0
void clr(int i) {
    a[i>>SHIFT] &= ~(1<<(i & MASK));
}
//test 测试所在的bit为是否为1
int  test(int i){
    return a[i>>SHIFT] &   (1<<(i & MASK));
}

int main()
{   int i;
    for (i = 0; i < N; i++)
        clr(i);
    while (scanf("%d", &i) != EOF)
        set(i);
    for (i = 0; i < N; i++)
        if (test(i))
            printf("%d\n", i);
    return 0;
}

#define BITSPERWORD 32

#define SHIFT 5

#define MASK 0x1F

#define N 10000000



int a[1 + N/BITSPERWORD];//申请内存的大小





//set 设置所在的bit位为1

void set(int i) {        

	a[i>>SHIFT] |=  (1<<(i & MASK)); 

}

//clr 初始化所有的bit位为0

void clr(int i) {        

	a[i>>SHIFT] &= ~(1<<(i & MASK)); 

}

//test 测试所在的bit为是否为1

int  test(int i){ 

	return a[i>>SHIFT] &   (1<<(i & MASK)); 

}



int main()

{	int i;

	for (i = 0; i < N; i++)

		clr(i);  

	while (scanf("%d", &i) != EOF)

		set(i);

	for (i = 0; i < N; i++)

		if (test(i))

			printf("%d\n", i);

	return 0;

}

 

注明： 左移n位就是乘以2的n次方，右移n位就是除以2的n次方

解析本例中的void set(int i) {        a[i>>SHIFT] |=  (1<<(i & MASK)); } 1)  i>>SHIFT： 其中SHIFT=5，即i右移5为，2^5=32,相当于i/32，即求出十进制i对应在数组a中的下标。比如i=20，通过i>>SHIFT=20>>5=0 可求得i=20的下标为0；
2)  i & MASK： 其中MASK=0X1F,十六进制转化为十进制为31，二进制为0001 1111，i&（0001 1111）相当于保留i的后5位。
比如i=23，二进制为：0001 0111，那么                          0001 0111                    &    0001 1111 = 0001 0111 十进制为：23 比如i=83，二进制为：0000 0000 0101 0011，那么                           0000 0000 0101 0011                      &   0000 0000 0001 0000 = 0000 0000 0001 0011 十进制为：19
i & MASK相当于i%32。
3) 1<<(i & MASK) 相当于把1左移 (i & MASK)位。 比如(i & MASK)=20，那么i<<20就相当于：          0000 0000 0000 0000 0000 0000 0000 0001 << 20        =0000 0000 0001 0000 0000 0000 0000 0000

 

注意上面 “|=”.

在博文：位运算符及其应用 提到过这样位运算应用：

将int型变量a的第k位清0，即a=a&~(1<<k) 将int型变量a的第k位置1， 即a=a|(1<<k)

这里的将  a[i/32] |= (1<<M)); 第M位置1 .

4) void set(int i) {        a[i>>SHIFT]  |=  (1<<(i & MASK)); }等价于：

void set(int i)
{
   a[i/32] |= (1<<(i%32));
}

void set(int i) 

{ 

   a[i/32] |= (1<<(i%32)); 

}

 

即实现上面提到的三步：

1.求十进制0-N对应在数组a中的下标： n/32

2.求0-N对应0-31中的数： N%32=M

3.利用移位0-31使得对应32bit位为1: 1<<M，并置1;

php实现是一样的：

 

<?php
  error_reporting(E_ERROR);
define("MASK", 0x1f);//31
define("BITSPERWORD",32);
define("SHIFT",5);
define("MASK",0x1F);
define("N",1000);

$a = array();
//set 设置所在的bit位为1
function set($i) {
    global $a;
    $a[$i>>SHIFT] |=  (1<<($i & MASK));
}
//clr 初始化所有的bit位为0
function clr($i) {
    $a[$i>>SHIFT] &= ~(1<<($i & MASK));
}
//test 测试所在的bit为是否为1
function test($i){
    global $a;
    return $a[$i>>SHIFT] & (1<<($i & MASK));
}
$aa = array(1,2,3,31, 33,56,199,30,50);
while ($v =current($aa))  {
   set($v);
   if(!next($aa)) {
       break;
   }
}
foreach ($a as $key=>$v){
    echo $key,'=', decbin($v),"\r\n";
}

<?php  

  error_reporting(E_ERROR);

define("MASK", 0x1f);//31  

define("BITSPERWORD",32);   

define("SHIFT",5);  

define("MASK",0x1F); 

define("N",1000); 



 $a = array(); 

//set 设置所在的bit位为1  

function set($i) {   

    global $a;       

    $a[$i>>SHIFT] |=  (1<<($i & MASK));   

}  

//clr 初始化所有的bit位为0  

function clr($i) {          

    $a[$i>>SHIFT] &= ~(1<<($i & MASK));   

}  

//test 测试所在的bit为是否为1  

function test($i){  

    global $a;  

    return $a[$i>>SHIFT] & (1<<($i & MASK));   

}  

$aa = array(1,2,3,31, 33,56,199,30,50);  

while ($v =current($aa))  {

   set($v); 

   if(!next($aa)) {

       break;

   }

}

foreach ($a as $key=>$v){

    echo $key,'=', decbin($v),"\r\n";

}

然后我们打印结果：

 

0=11000000000000000000000000001110 1=1000001000000000000000010 6=10000000

32位表示，实际结果一目了然了，看看1,2,3,30,31, 33,50，56,199数据所在的具体位置：

       31    30                                                                                        3     2     1

                                                                                             

0=    1     1    00       0000   0000   0000   0000    0000     0000   1     1   1  0

                         56                 50                                                33

                                                                                           1=  0000     0001    0000   0100   0000    0000     0000    0010

                                                                               199

                                                                              6=  0000  0000    0000   0000   0000    0000    1000    0000

 

 

【问题实例】

已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数。

8位最多99 999 999，大概需要99m个bit，大概10几m字节的内存即可。 （可以理解为从0-99 999 999的数字，每个数字对应一个Bit位，所以只需要99M个Bit==1.2MBytes，这样，就用了小小的1.2M左右的内存表示了所有的8位数的电话）
2)2.5亿个整数中找出不重复的整数的个数，内存空间不足以容纳这2.5亿个整数。 将bit-map扩展一下，用2bit表示一个数即可，0表示未出现，1表示出现一次，2表示出现2次及以上，在遍历这些数的时候，如果对应位置的值是0，则将其置为1；如果是1，将其置为2；如果是2，则保持不变。或者我们不用2bit来进行表示，我们用两个bit-map即可模拟实现这个2bit-map，都是一样的道理。

实现：

 

// TestWin32.cpp : Defines the entry point for the console application.
#include "stdafx.h"

#include<memory.h>

//用char数组存储2-Bitmap,不用考虑大小端内存的问题
unsigned char flags[1000]; //数组大小自定义
unsigned get_val(int idx)  {
//  |    8 bit  |
//  |00 00 00 00|  //映射3 2 1 0
//  |00 00 00 00|  //表示7 6 5 4
//  ……
//  |00 00 00 00|

    int i = idx/4;  //一个char 表示4个数，
    int j = idx%4;
    unsigned ret = (flags[i]&(0x3<<(2*j)))>>(2*j);
    //0x3是0011 j的范围为0-3，因此0x3<<(2*j)范围为00000011到11000000 如idx=7 i=1 ,j=3 那么flags[1]&11000000, 得到的是|00 00 00 00|
    //表示7 6 5 4
   return ret;
}

unsigned set_val(int idx, unsigned int val)  {
    int i = idx/4;
    int j = idx%4;
    unsigned tmp = (flags[i]&~((0x3<<(2*j))&0xff)) | (((val%4)<<(2*j))&0xff);
    flags[i] = tmp;
    return 0;
}
unsigned add_one(int idx)
{
    if (get_val(idx)>=2) {  //这一位置上已经出现过了？？
        return 1;
    }  else  {
        set_val(idx, get_val(idx)+1);
        return 0;
    }
}

//只测试非负数的情况;
//假如考虑负数的话,需增加一个2-Bitmap数组.
int a[]={1, 3, 5, 7, 9, 1, 3, 5, 7, 1, 3, 5,1, 3, 1,10,2,4,6,8,0};

int main()   {
    int i;
    memset(flags, 0, sizeof(flags));

    printf("原数组为:");
    for(i=0;i < sizeof(a)/sizeof(int); ++i)  {
        printf("%d  ", a[i]);
        add_one(a[i]);
    }
    printf("\r\n");

    printf("只出现过一次的数:");
    for(i=0;i < 100; ++i)  {
        if(get_val(i) == 1)
            printf("%d  ", i);
        }
    printf("\r\n");

    return 0;
}