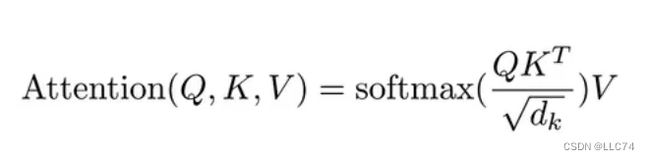Attention +Transformer学习记录（二）

目录

a.注意力机制和自注意力机制的区别

b.引入自注意力机制的原因

c.计算公式

d.代码实现

二、Multi-Head Attention

1.Multi-Head Attention的计算

2.位置编码

三、Transformer模型

1.Transformer整体结构

2.Transformer的input输入

2.1如何获得位置编码？

3.Transformer的Encoder

3.1Add＆Normalize

3.2ResNet残差神经网络

3.3Normalize

3.4全连接层

4.Transformer的Decoder

4.1Decoder的输入

a.训练时的输入

b.预测时的输入

4.2Masked Multi-Head Attention

a.Padding mask

b.sequence mask

4.3基于Encoder-Decoder的Multi-Head Attention

5.Transformer的输出

---

一、Self-Attention

参考论文：原创 | Attention is all you need 论文解析（附代码）

自注意力机制(Self-Attention)_Michael_Lzy的博客-CSDN博客

参考视频：self-Attention｜自注意力机制 ｜位置编码 ｜ 理论 + 代码_哔哩哔哩_bilibili

a.注意力机制和自注意力机制的区别

Attention机制中的权重的计算需要Target来参与。即在Encoder-Decoder 模型中，Attention权值的计算不仅需要Encoder中的隐状态而且还需要Decoder中的隐状态。

self-attention机制不是输入语句和输出语句之间的Attention机制，而是输入语句内部元素之间或者输出语句内部元素之间发生的Attention机制。例如在Transformer中在计算权重参数时，将文字向量转成对应的KQV，只需要在Source处进行对应的矩阵操作，用不到Target中的信息。

b.引入自注意力机制的原因

神经网络接受很多长短不一的向量，并且向量与向量之间存在关系，但实际常常因为不能充分发挥这些输入之间的关系从而导致训练效果变差。self-attention让机器注意到这些输入之间的相关性。

c.计算公式

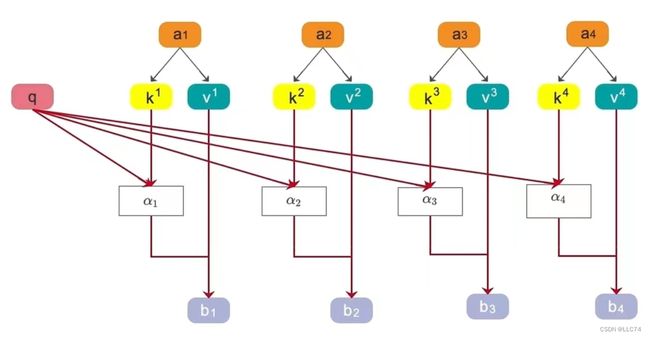
q--查询的问题 ，k--商品标签，a--相似度 ， v--商品评价 ， b--商品总分

如何理解self ?

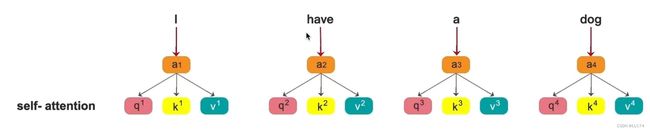
self-attention 中的self，表示 q , k , v 都来自于自己，每个token（a)都能提取出自己的q、k、v。

q、k:从每个token中提取出，反映对token的理解。若要获取a1与其他词的相似度，则用a1的q与其他词的k相乘；q是主动获取与其他token的相似度，k是被动。

v:表示当前token的重要程度（比如在本句中，'I'和'dog'的value较高）

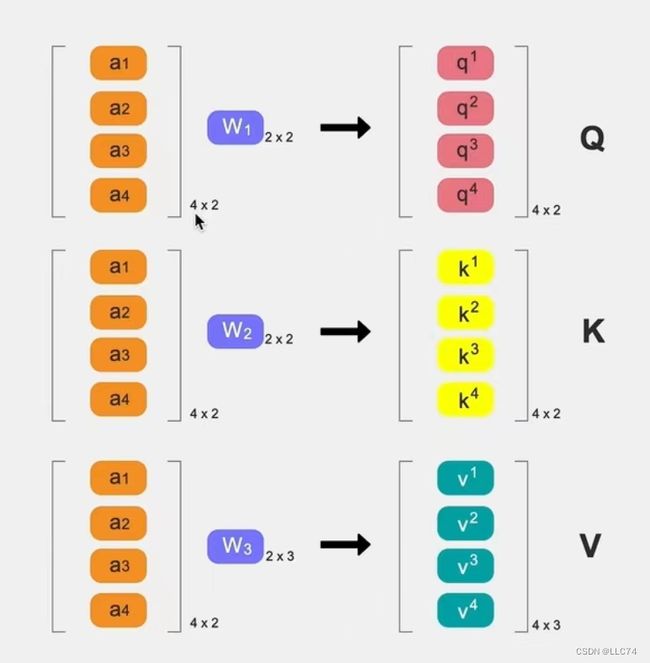
举例：假设a1,a2,a3,a4均为embedding之后的向量

四个token共用一套w1,w2,w3

q、k的维度为2，v的维度为3，dk是k的长度，即为2

d.代码实现

class Self_Attention(nn,Moudle):
     def __init__(self,dim,dk,dv):
         super(self_Attention,self).__init__
         self.scale = dk ** -0.5
         self.q = nn.Linear(dim, dk)
         self.k = nn.Linear(dim, dk)//q,k的输出维度要保持一致
         self.v = nn.Linear(dim, dv)//三个全连接层，从输入中提取q,k,v
     

     def forward(self,x):
         q = self.q(x)//q = {Tensor:(1,4,2)}
         k = self.k(x)//k = {Tensor:(1,4,2)}
         v = self.v(x)//k = {Tensor:(1,4,3)}
         

         attn = (q @ k.transpose(-2，-1)) * self.scale
         attn = attn.softmax(dim=-1)
         

         x = attn @ v
         return x


att = self_Attention(dim=2,dk=2,dv=3)
x = torch.rand((1,4,2))//随机得出，1是batchsize,4是4个token,2是每个token的长度
output = att(x)

二、Multi-Head Attention

参考原文：详解Transformer中Self-Attention以及Multi-Head Attention-CSDN博客

1.Multi-Head Attention的计算

原论文提到：Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.多头注意力机制可以联合来自不同head部分学习到的信息。

和Self-Attention一样，首先将ai通过Wq,Wk,Wv，得到对应的qi,ki,vi，然后根据head的数目h，将qi,ki,vi均分成h份。例如，以下是2个head的情况：

h=1时，q1被分为了q(1,1)和q(1,2),q(1,1)属于head1,q(1,2)属于head2.

用上述方法便可得到每个head对应的q,k,v，针对每个head的q,k,v和Self-Attention计算方法即可得到对应的结果。

接下来将每个head得到的结果进行concat拼接，head1得到的b1和head2得到的b1拼接在一起，head1得到的b2和head2得到的b2拼接在一起，最后将拼接的结果通过W（可学习的参数）融合在一起，得到最终的结果b1,b2。

代码实现：

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        #在类的初始化时，会传入三个参数，h代表头数，d_model代表词嵌入的维度，dropout代表进行dropout操作时置0比率，默认是0.1
        super(MultiHeadedAttention, self).__init__()
        #在函数中，首先使用了一个测试中常用的assert语句，判断h是否能被d_model整除，这是因为我们之后要给每个头分配等量的词特征，也就是embedding_dim/head个
        assert d_model % h == 0
        #得到每个头获得的分割词向量维度d_k
        self.d_k = d_model // h
        #传入头数h
        self.h = h
        
        #创建linear层，通过nn的Linear实例化，它的内部变换矩阵是embedding_dim x embedding_dim，然后使用，为什么是四个呢，这是因为在多头注意力中，Q,K,V各需要一个，最后拼接的矩阵还需要一个，因此一共是四个
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        #self.attn为None，它代表最后得到的注意力张量，现在还没有结果所以为None
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, query, key, value, mask=None):
        #前向逻辑函数，它输入参数有四个，前三个就是注意力机制需要的Q,K,V，最后一个是注意力机制中可能需要的mask掩码张量，默认是None
        if mask is not None:
            # Same mask applied to all h heads.
            #使用unsqueeze扩展维度，代表多头中的第n头
            mask = mask.unsqueeze(1)
        #接着，我们获得一个batch_size的变量，他是query尺寸的第1个数字，代表有多少条样本
        nbatches = query.size(0)
        
        # 1) Do all the linear projections in batch from d_model => h x d_k 
        # 首先利用zip将输入QKV与三个线性层组到一起，然后利用for循环，将输入QKV分别传到线性层中，做完线性变换后，开始为每个头分割输入，这里使用view方法对线性变换的结构进行维度重塑，多加了一个维度h代表头，这样就意味着每个头可以获得一部分词特征组成的句子，其中的-1代表自适应维度，计算机会根据这种变换自动计算这里的值，然后对第二维和第三维进行转置操作，为了让代表句子长度维度和词向量维度能够相邻，这样注意力机制才能找到词义与句子位置的关系，从attention函数中可以看到，利用的是原始输入的倒数第一和第二维，这样我们就得到了每个头的输入
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]
 
        # 2) Apply attention on all the projected vectors in batch. 
        # 得到每个头的输入后，接下来就是将他们传入到attention中，这里直接调用我们之前实现的attention函数，同时也将mask和dropout传入其中
        x, self.attn = attention(query, key, value, mask=mask, 
                                 dropout=self.dropout)
 
        # 3) "Concat" using a view and apply a final linear. 
        # 通过多头注意力计算后，我们就得到了每个头计算结果组成的4维张量，我们需要将其转换为输入的形状以方便后续的计算，因此这里开始进行第一步处理环节的逆操作，先对第二和第三维进行转置，然后使用contiguous方法。这个方法的作用就是能够让转置后的张量应用view方法，否则将无法直接使用，所以，下一步就是使用view重塑形状，变成和输入形状相同。  
        x = x.transpose(1, 2).contiguous() \
             .view(nbatches, -1, self.h * self.d_k)
        #最后使用线性层列表中的最后一个线性变换得到最终的多头注意力结构的输出
        return self.linears[-1](x)

2.位置编码

Self-Attention和Multi-Head Attention模块在计算中是没有考虑到位置信息的，在Self-Attenntion中，输入a1,a2,a3，得到b1,b2,b3。对于a1而言，a2,a3与a1之间的距离是一样近的，且没有先后顺序。如果将输入改成a1,a3,a2，对结果b1是没有影响的。

为了引入位置信息，原论文中引入了位置编码，

如图所示，位置编码直接加在输入a={a1,a2,...,an}中，即pe={pe1,pe2,...,pen}，它和a有相同的维度。关于位置编码，在原论文中有提出两种方案，一种是原论文中使用的固定编码，即论文中给出的sine and cosine functions方法，按照该方法可计算出位置编码；另一种是可训练的位置编码，作者说尝试了两种方法发现结果差不多。

代码实现：

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout, max_len=5000):
        """
        位置编码器类的初始化函数
        
        共有三个参数，分别是
        d_model：词嵌入维度
        dropout: dropout触发比率
        max_len：每个句子的最大长度
        """
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)
        
        # Compute the positional encodings
        # 注意下面代码的计算方式与公式中给出的是不同的，但是是等价的，你可以尝试简单推导证明一下。
        # 这样计算是为了避免中间的数值计算结果超出float的范围，
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) *
                             -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)
        
    def forward(self, x):
        x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
        return self.dropout(x)

三、Transformer模型

参考文章：史上最小白之Transformer详解_transformer最小白-CSDN博客

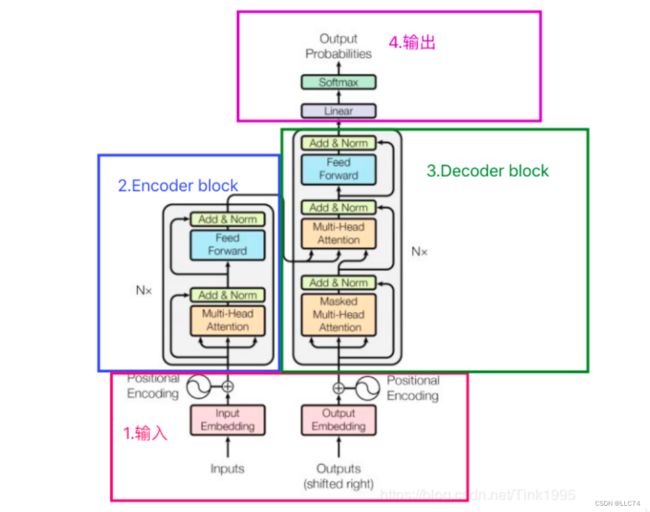
1.Transformer整体结构

Transformer是一个基于Encoder-Decoder框架的模型，主要分为以上四个模块，其中Encoder block 和Deconder block两部分比较重要。

2.Transformer的input输入

以"Tom chase Jerry"为例，input即输入该句分词后的词向量，可以是任意形式的词向量。

图中，输入input embedding后，又给每个word的词向量添加了位置编码：因为词的位置不同会导致语义发生极大的变化，我们的Transformer是完全基于Self-Attention之上的，而Self-Attention不含位置编码。

2.1如何获得位置编码？

可以通过数据训练学习得到positional encoding，类似于训练学习词向量，goole在之后的bert中的positional encoding便是由训练得到的。

3.Transformer的Encoder

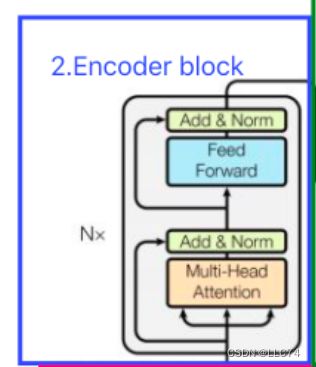      一个enconder block由6个enconder构成，图中灰色部分是一个enconder结构，其中Nx=6。一个Enconder部分由一个Multi-Head Attention和一个全连接神经网络Feed Forward Network构成。                                                          通过Multi-Head Attention 得到矩阵Z之后并不是直接传入全连接神经网络FNN，而是进行了一步Add-Normalize。

3.1Add＆Normalize

Add:就是在矩阵Z上面加了一个残差块X（Transformer里加上的X就是Multi-Head Attention里输入的矩阵X），目的是防止深度神经网络在训练中发生退化问题。

退化：即深度神经网络通过增加网络层数，Loss逐渐减小，然后趋于饱和达到稳定，随着网络层数继续增加，Loss反而增大。

退化的原因：比如某个神经网络的最优层数是16层，但是我们在设计的时候不知道有多少层，我们假定设计32层，那么多出来16层，所以我们需要让多出来的16层进行恒等映射（即F(x)=x），才能让这多出来的16层不会对此神经网络产生影响。

多余的层数一多，影响就很明显了，所以提出了ResNet残差神经网络来解决此问题。

3.2ResNet残差神经网络

如图是一个残差块，x为残差块的输入，x经过一轮线性变化并激活输出得到F(x)，F(x)进行第二轮的线性变化，然后加上x，进行激活输出。此路径被称为shortcut连接。

此时，要完成恒等映射的函数就变成了H(x)=F(x)+x，要使得H(x)=x，则使F(x)=0，因为一般初始化神经网络的参数就是【0，1】的随机数，使F(x)=0比使F(x)=x简单地多。

3.3Normalize

在神经网络进行训练之前，都要对数据进行Normalize归一化，有两个目的：1.加快训练的速度2.提高训练的稳定性。

LN是在同一样本中不同位置的神经元进行归一化，BN是在不同样本中同一位置的神经元进行归一化，即将同一维度的神经元进行归一化。我们选择使用LN，是因为在NLP中，输入的都是词向量，单独分析它的每一维是没有意义的。

3.4全连接层

此为全连接层公式： 

FFN(x)=max(0,xW1​+b1​)W2​+b2​

该全连接层是一个两层的神经网络，先进行线性变换，再进行ReLU非线性变换，最后进行线性变换。此时的x就是Multi-Head Attention的输出矩阵Z。这两层映射到更高维的空间中，再进行非线性ReLU筛选，筛选回原来的维度。最后进行Add-Normalize进入到Decoderc层。

4.Transformer的Decoder

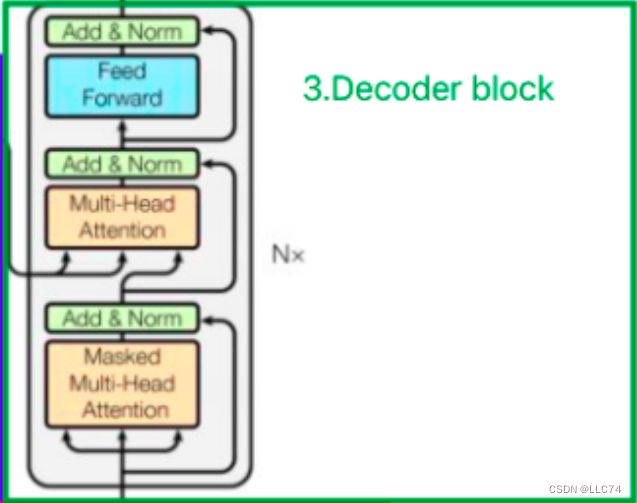一个Decoder block 由6个Decoder构成，其中Nx=6。一个Decoder由Masked Multi-Head Attention、Multi-Head Attention、全连接神经网络FNN构成。

4.1Decoder的输入

a.训练时的输入

例如：Encoder输入："Tom chase Jerry"，Decoder输入"汤姆追逐杰瑞"。

b.预测时的输入

从起始符开始，每一次的输入都是上一次Transformer的输出。

例如：输入起始符" "，输出"汤姆"，输入"汤姆"，输出"汤姆追逐"，直到输出"汤姆追逐杰瑞"为止。

4.2Masked Multi-Head Attention

Masked表示掩码，它对某些值进行掩盖，使其在参数更新时不产生效果。

Encoder中也需要mask,不过只需用到Padding mask。

a.Padding mask

由于输入序列的长度不一样，为了对齐，常常会在较短的序列后添加0，对于较长的序列，常常会删掉其左边多余的部分，因为这些填充的位置通常是无意义的，所以不该把attention放在他们身上。一般情况下，会在这些位置上加上一个无穷大的非负数值，经过softmax处理后，这些位置会接近0。

b.sequence mask

sequence mask使Decoder不能看见未来的信息，对一个序列，在step_time为t的时候，我们的解码输出只能依赖于t时刻前的输出，所以要将t时刻后的信息隐藏起来，这只在训练的时候有效，因为训练的时候我们会将Target数据完整地输入Decoder中。

那预测的时候怎么办呢？

只需要产生一个上三角的值全部为0的矩阵，作用在每一个序列上。

4.3基于Encoder-Decoder的Multi-Head Attention

Encoder中的Multi-Head Attention是基于self-Head Attention，Decoder中的Multi-Head Attention仅基于Attention，它的输入Q来自于Masked Multi-Head Attention的输出，K和V来自于Encoder最后一层的输出。

 Masked Multi-Head Attention是为了得到之前已经预测出的信息，Multi-Head Attention是输入已经预测到的信息，继续预测得到下一刻的信息，即输出信息。

5.Transformer的输出

经过一次Linear，再进行softmax得到输出的概率分布，通过词典，概率最大所对应的单词则为下一次的输出。

思考：Transformer虽然速度快，效果好，但还存在一定的问题。词语位置信息间有存在丢失，即使加入了positional encoding，但还存在可优化的地方。