信号系统之神经网络

1 目标检测

科学家和工程师经常需要知道是否存在特定的物体或条件。例如，地球物理学家在地球上探索石油，医生检查病人是否有疾病，天文学家在宇宙中寻找外星智慧，等等。这些问题通常涉及将采集的数据与阈值进行比较。如果超过阈值，则视为存在目标（所寻求的对象或条件）。

例如，假设发明了一种用于检测人类癌症的设备。该设备在患者身上挥舞，视频屏幕上会弹出一个 介于 0 和 30 之间的数字。低数字对应于健康受试者，而高数字表示存在癌组织。发现该设备运行良好，但并不完美，偶尔会出错。问题是：如何使用这个系统来造福被检查的患者？

图 26-1 说明了分析这种情况的系统方法。假设该设备在两组上进行测试：数百名已知健康的志愿者（非目标）和数百名已知患有癌症的志愿者（目标）。图（a）和（b）显示了这些测试结果，显示为直方图。健康受试者通常比患有癌症的受试者产生更少的数量（好），但两种分布之间存在一些重叠（坏）。

直方图可以用作**概率分布函数（pdf）**的估计值，如（c）所示。例如，假设该设备用于随机选择的健康受试者。从（c）开始，大约有 8% 的几率是 3，大约 1% 的几率是 18，依此类推。

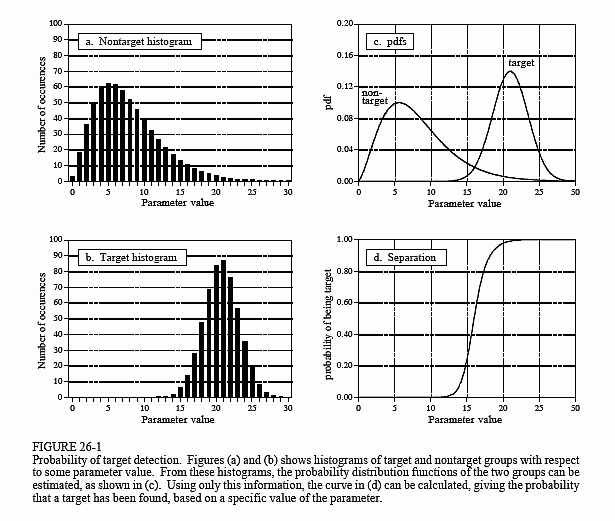
当该设备用于健康状况未知的患者时会发生什么？ 例如，如果一个以前从未见过的人收到值 15，可以得出什么结论？他们是否患有癌症？我们知道，一个健康人产生 15 的概率是 2.1%。同样，癌症患者有 0.7% 的几率会产生 15。如果没有其他信息，会得出结论，受试者不患癌症的可能性是患癌症的三倍。也就是说，测试结果 15 意味着受试者来自目标群体的概率为 25%。这种方法可以推广为形成（d）中的曲线，即受试者患癌症的概率仅基于设备产生的数量[数学上，$pd{f}_t/(pd{f}_t+pd{f}_{nt})$]。

如果在这一点上停止分析，将犯目标检测中最常见错误之一。通常必须考虑另一个信息来源，以使（d）中的曲线有意义。这是要测试的人群中目标与非目标的相对数量。例如，可能会发现，每千人中只有一人患有试图检测的癌症。为了将其包含在分析中，调整（c）中非目标pdf的振幅，使曲线下面积为0.999。同样，调整目标 pdf 的振幅，使曲线下的面积为 0.001。然后像以前一样计算图（d），以给出患者患癌症的概率。

忽略此信息是一个严重的错误，因为它极大地影响了测试结果的解释方式。换言之，当包括患病率信息时，图（d）中的曲线发生了巨大变化。例如，如果患有癌症的人口比例为 0.001，则测试结果为 15 仅对应于该患者患有癌症的概率为 0.025%。这与仅依靠机器输出发现的 25% 概率有很大不同。

这种将输出值转换为概率的方法对于理解问题很有用，但它不是完成目标检测的主要方式。大多数应用程序需要对以下方面做出是/否决定目标的存在，因为“是”将导致一个动作，而“否”将导致另一个动作。这是通过将测试的输出值与阈值进行比较来完成的：

• 如果输出高于阈值，则称测试为阳性，表明目标存在。
• 如果输出低于阈值，则称测试为阴性，表明目标不存在。

在癌症例子中，阴性检测结果意味着患者被告知他们很健康，并被送回家。当检测结果呈阳性时，将进行额外的检测，例如通过插入活检针获取组织样本。

由于目标分布和非目标分布重叠，因此某些测试结果将不正确。也就是说，一些被送回家的病人实际上会患有癌症，而一些被送去做额外检查的病人会很健康。在目标检测的术语中，正确的分类称为 true，而不正确的分类称为 false。例如，如果患者患有癌症，并且测试正确检测到病情，则称为真阳性。同样，如果患者没有癌症，并且测试表明不存在癌症，则称为真阴性。当患者没有癌症，但测试错误地表明他们有癌症时，就会发生假阳性。这导致了不必要的担忧，以及额外测试的痛苦和费用。更糟糕的情况发生在假阴性的情况下，存在癌症，但测试表明患者是健康的。

这两种错误造成的人类痛苦使阈值选择成为一种微妙的平衡行为。可以容忍多少个假阳性来减少假阴性的数量？ 图 26-2 显示了评估此问题的图形方法，即 ROC 曲线（Receiver Operating Characteristic 的缩写）。ROC 曲线绘制了各种阈值值下报告为正的目标信号的百分比（越高越好）与错误报告为正的非目标信号的百分比（越低越好）。换言之，ROC 曲线上的每个点都代表了真阳性和假阳性性能的一种可能权衡。

图（a）至（d）显示了癌症检测示例中阈值的四种设置。例如，查看 （b） 中的阈值设置为 17。请记住，每个产生大于阈值的输出值的测试都会报告为阳性结果。非目标分布面积的约13%大于阈值（即阈值右侧）。在所有没有癌症的患者中，87% 将报告为阴性（即真阴性），而 13% 将报告为阳性（即假阳性）。相比之下，目标分布的面积约为80%大于阈值。这意味着 80% 的癌症患者将产生阳性检测结果（即真阳性）。另外 20% 患有癌症的人将被错误地报告为阴性（即假阴性）。如（b）中的ROC曲线所示，该阈值导致曲线上的一个点为：%nontargets positive=13%，%targets positive=80%。

检测过程越高效，ROC曲线向图形左上角弯曲的程度就越大。纯粹的猜测结果是一条对角线为 45° 的直线。如（a）所示，将阈值设置得相对较低，几乎可以检测到所有目标信号。这是以许多误报为代价的。如（d）所示，将阈值设置得相对较高会提供相反的情况：误报很少，但错过目标很多。

此分析可以扩展到提供多个输出的设备。例如，假设癌症检测系统通过拍摄受试者的 X 射线图像来运行，然后使用自动图像分析算法来识别肿瘤。这些算法识别可疑区域，然后测量关键特征以帮助评估。例如，假设测量可疑区域的直径（参数 1）及其在图像中的亮度（参数 2）。进一步假设我们的研究表明，肿瘤通常比正常组织更大、更亮。作为第一次尝试，可以对每个参数进行前面介绍的 ROC 分析，并为每个参数找到一个可接受的阈值。然后，只有当测试满足两个条件时，才能将测试归类为阳性：参数 1 大于某个阈值，参数 2 大于另一个阈值。

这种分别对参数进行阈值化然后调用逻辑函数（AND、OR 等）的技术非常常见。然而，它的效率非常低，并且有更好的方法。图 26-3 显示了为什么会出现这种情况。在此图中，每个三角形代表一个目标（癌症患者）的单个出现，该目标绘制在与其两个参数值相对应的位置。同样，每个方块代表非目标（没有癌症的患者）的单次出现。如pdf所示图表在每个轴的一侧，两个参数在目标分布和非目标分布之间有很大的重叠。换句话说，每个参数单独来看，都是癌症的不良预测指标。将这两个参数与简单的逻辑功能相结合只会提供很小的改进。这特别有趣，因为这两个参数包含将目标与非目标完美分开的信息。这是通过在两组之间绘制一条对角线来完成的，如图所示。

在行话中，这种类型的坐标系称为参数空间。例如，此示例中的二维平面可称为直径-亮度空间。这个想法是目标将占据参数空间的一个区域，而非目标将占据另一个区域。两个区域之间的分离可能像一条直线一样简单，也可能像具有不规则边界的封闭区域一样复杂。图 26-4 显示了下一个复杂度级别，即在 x、y 和 z 轴 上表示的三个参数空间。例如，这可能对应于 测量直径、亮度和第三个参数（例如边缘锐度） 的癌症检测系统。就像在二维情况下一样，重要的想法是目标和非目标群体的成员将占据空间的不同区域，从而将两者分开。在三维空间中，区域由平面和曲面分隔。术语超空间（超过、高于或超出正常空间）通常用于描述具有三维以上的参数空间。从数学上讲，超空间与一维空间、二维空间和三维空间没有什么不同；然而，它们有一个实际问题，即无法在三维宇宙中以图形形式显示。

为单个参数问题选择的阈值（通常）不能归类为正确或错误。这是因为每个阈值都会导致假阳性和假阴性的唯一组合，即沿 ROC 曲线的某个点。这是用一个目标换另一个目标，没有绝对正确的答案。另一方面，具有两个或多个参数的参数空间肯定会在区域之间有错误的划分。例如，想象一下增加图 26-3 中的数据点数量，显示目标组和非目标组之间的小重叠。可以在组之间移动阈值线，以将误报数与假阴性数进行交换。也就是说，对角线将向右上角或左下角移动。但是，旋转线是错误的，因为它会增加两种类型的错误。

正如这些示例所表明的，传统的目标检测方法（有时称为模式识别）是一个两步过程:

• 第一步称为特征提取。这使用算法将原始数据减少到几个参数，例如直径、亮度、边缘锐度等。这些参数通常称为要素或分类器。需要进行特征提取以减少数据量。例如，医疗 X 射线图像可能包含超过 100 万像素。特征提取的目标是将信息提炼成更集中、更易于管理的形式。
• 在第二步中，对分类器进行评估，以确定目标是否存在。换句话说，使用某种方法将参数空间划分为与目标相对应的区域和与非目标相对应的区域。这对于单参数和双参数空间来说非常简单;已知数据点绘制在图表上（如图 26-3），区域用眼睛分隔。然后将除法作为方程式写入计算机程序，或者以其他方式定义一个区域与另一个区域。原则上，这种相同的技术可以应用于三维参数空间。问题是，三维图形很难被人类理解和可视化（如图26-4）。注意：不要在超空间中尝试此操作。

简而言之，需要一台可以根据目标和非目标信号示例进行多参数空间划分的机器。这种理想的目标检测系统非常接近本章的主题，即神经网络。

### 2 神经网络架构

人类和其他动物使用神经网络处理信息。它们是由数万亿个神经元（神经细胞）交换称为动作电位的短暂电脉冲形成的。模仿这些生物结构的计算机算法被正式称为人工神经网络。

神经网络研究的动机有两个：更好地了解人脑，以及开发能够处理抽象和定义不明确的问题的计算机。例如，传统计算机在理解语音和识别人脸方面存在困难。相比之下，人类在这些任务上做得非常好。

神经网络最常用的结构如图26-5所示。该神经网络由三层组成，分别称为输入层、隐藏层和输出层。每个图层由一个或多个节点组成，在此图中由小圆圈表示。节点之间的线表示信息从一个节点到下一个节点的流动。在这种特殊类型的神经网络中，信息仅从输入流向输出（即从左到右）。其他类型的神经网络具有更复杂的连接，例如反馈路径。

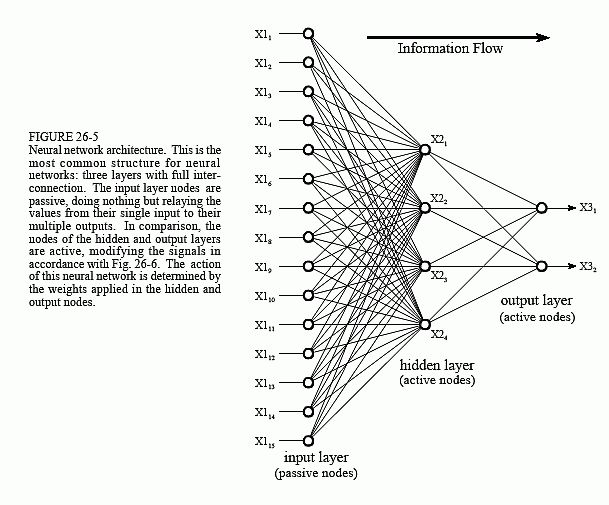
输入层的节点是被动的，这意味着它们不会修改数据。他们在输入时接收一个值，并将该值复制到它们的多个输出。相比之下，隐藏层和输出层的节点处于活动状态，这意味着他们修改了数据，如图 26-6 所示。变量： $X{1}_1，X{1}_2...X{1}_{15}$ 保存要评估的数据（见图 26-5），它们可能是来自图像的像素值、来自音频信号的样本、连续几天的股票市场价格等。它们也可能是其他一些算法的输出，例如癌症检测示例中的分类器：直径、亮度、边缘锐度等。

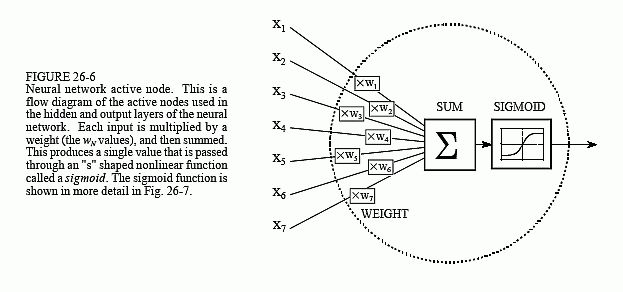
输入图层中的每个值都会被复制并发送到所有隐藏节点。这称为完全互连的结构。如图 26-6 所示，进入隐藏节点的值乘以权重，权重是存储在程序中的一组预定数字。然后将加权输入相加以生成单个数字。这在图中用符号 ∑ 表示。在离开节点之前，该数字将通过称为 sigmoid 的非线性数学函数传递。这是一条“s”形曲线，用于限制节点的输出。也就是说，sigmoid 的输入值介于 -∞ 和 +∞ 之间，而其输出只能介于 0 和 1 之间。

隐藏层的输出在流程图（图 26-5）中由变量表示：$X{2}_1、X{2}_2、X{2}_3和X{2}_4$ 。和以前一样，这些值中的每一个都会被复制并应用于下一层。输出层的有源节点组合并修改数据以生成该网络的两个输出值 $X{3}_1和X{3}_2$。

神经网络可以具有任意数量的层，每层可以具有任意数量的节点。大多数应用程序使用三层结构，最多有几百个输入节点。隐藏层的大小通常约为输入层的 10%。在目标检测的情况下，输出层只需要一个节点。此节点的输出是阈值的，以提供输入数据中目标存在或不存在的正或负指示。

表26-1是执行图26-5的流程图的程序。关键是这个架构非常简单，非常通用。同样的流程图可以用于许多问题，无论它们的特殊怪癖如何。神经网络提供有用的数据操作的能力在于权重的正确选择。这与传统的信息处理截然不同，在传统的信息处理中，解决方案是在分步程序中描述的。

例如，想象一个用于识别声纳信号中物体的神经网络。假设来自信号的 1000 个样本存储在计算机中。计算机如何确定这些数据是否代表潜艇、鲸鱼、海底山脉，或者什么都不代表？传统的DSP将通过数学和算法来解决这个问题，例如相关性和频谱分析。使用神经网络，只需将 1000 个样本输入层，即可从输出层弹出值。通过选择适当的权重，可以将输出配置为报告各种信息。例如，可能有以下输出：潜艇（是/否）、鲸鱼（是/否）、海底山脉（是/否）等。

使用其他权重，输出可能会将对象分类为：金属或非金属、生物或非生物、敌人或盟友等。没有算法，没有规则，没有程序；只有输入和输出之间的关系，由所选权重的值决定。

图 26-7a 显示了对 sigmoid 函数的仔细观察，该函数在数学上由以下公式描述：

sigmoid 的确切形状并不重要，重要的是它是一个平滑的阈值。为了进行比较，当 x>0 时，一个简单的阈值产生一个值 1，当 x<0 时，一个值产生一个 0 的值。sigmoid 执行相同的基本阈值功能，但也是可微的，如图 26-7b 所示。虽然流程图中没有使用导数（图 25-5），但它是找到合适权重的关键部分。sigmoid 的一个优点是有一个快捷方式来计算其导数的值：

例如，如果 x=0，则 s(x)=0.5（通过方程 26-1），并计算一阶导数：s’(x)=0.5(1-0.5)=0.25。这不是一个关键概念，只是一个使代数更短的技巧。

如果 sigmoid 可以向左或向右调整，使其以 x=0 以外的其他值为中心，神经网络会不会更灵活？答案是肯定的，大多数神经网络都允许这样做。实施起来非常简单；将向输入层添加一个附加节点，其输入值始终为 1。当此值乘以隐藏层的权重时，它会为每个 S 形数据提供偏置（直流偏移）。这种添加称为偏置节点。它的处理方式与其他节点相同，但常量输入除外。

神经网络可以在没有 S 形或类似非线性的情况下构建吗？要回答这个问题，请看图 26-5 的三层网络。如果 S 形不存在，则三层将collapse仅两层。换句话说，隐藏层和输出层的总和和权重可以合并为一个层，从而仅产生一个两层网络。

3 它为什么有效？

使神经网络执行特定任务所需的权重由学习算法找到，以及系统应如何运行的示例。例如，声纳问题中的示例是包含 1000 个样本段中的数百个（或更多）的数据库。一些示例段对应于潜艇，其他对应于鲸鱼，其他对应于随机噪声等。学习算法使用这些示例来计算一组适合手头任务的权重。术语学习在神经网络领域被广泛用于描述这一过程；但是，更好的描述可能是：根据示例的统计数据确定一组优化的权重。无论该方法叫什么，人类几乎都无法理解所得到的权重。在极少数情况下，模式可能是可以观察到的，但通常它们似乎是随机数。可以观察到使用这些权重的神经网络具有适当的输入/输出关系，但为什么这些特定的权重会起作用是相当令人困惑的。

尽管如此，经常听到神经网络倡导者发表这样的声明：“神经网络很好理解”。为了探索这一说法，我们将首先证明通过传统的DSP方法可以选择神经网络权重。接下来，将证明学习算法提供了比传统技术更好的解决方案。虽然这并不能解释为什么一组特定的权重会起作用，但它确实提供了对该方法的信心。

在最复杂的观点中，神经网络是一种在参数空间中标记各个区域的方法。例如，考虑具有 1000 个输入和单个输出的声纳系统神经网络。通过适当的权重选择，如果输入信号是来自潜艇的回波，则输出将接近 1，如果输入只是噪声，则输出将接近零。这形成了一个 1000 维的参数超空间。神经网络是一种为这个超空间中的每个位置分配一个值的方法。也就是说，1000 个输入值定义了超空间中的一个位置，而神经网络的输出则提供了该位置的值。查找表可以完美地执行此任务，为每个可能的输入地址存储一个输出值。不同之处在于，神经网络计算每个位置（地址）的值，而不是存储每个值的不可能完成的大型任务。事实上，神经网络架构通常通过它们在给定数量的权重下分离超空间的程度来评估。

这种方法还为隐藏层中所需的节点数提供了线索。N 维的参数空间需要 N 个数字来指定位置。识别超空间中的区域需要 2N 个值（即沿每个轴的最小值和最大值定义一个超空间矩形实体）。例如，这些简单的计算表明，具有 1000 个输入的神经网络需要 2000 个权重才能将超空间的一个区域与另一个区域区分开来。在完全互连的网络中，这将需要两个隐藏的节点。所需的区域数取决于特定问题，但可以预期远远小于参数空间中的维数。虽然这只是一个粗略的近似值，但它通常解释了为什么大多数神经网络可以在输入层大小为 2% 到 30% 的隐藏层的情况下运行。

一种完全不同的理解神经网络的方式使用DSP的相关性概念。相关性是检测信号中是否包含已知模式的最佳方法。它是通过将信号与要寻找的模式相乘，然后乘积来实现的。总和越高，信号越像模式。现在，检查图 26-5，并将每个隐藏节点视为在输入数据中寻找特定模式。也就是说，每个隐藏节点都将输入数据与与该隐藏节点关联的权重集相关联。如果存在该模式，则传递给 sigmoid 的总和将很大，否则会很小。

从这个角度来看，sigmoid 的作用非常有趣。回头看图 26-1d，注意到分隔两个钟形分布的概率曲线类似于 S 形分布。如果手动设计一个神经网络，可以使每个隐藏节点的输出是输入数据中存在特定模式的分数概率。输出层重复此操作，使整个三层结构成为相关性的关联，即查找模式的网络。

传统的 DSP 基于两种技术，卷积和傅里叶分析。神经网络可以执行这两种操作，以及更多操作。想象一下，一个 N 个样本信号被滤波以产生另一个 N 个样本信号。根据卷积的输出侧视图，输出信号中的每个样本都是来自输入的样本的加权和。想象一个两层神经网络，每层有 N 个节点。每个输出层节点生成的值也是输入值的加权和。如果每个输出层节点使用与所有其他输出节点相同的权重，则网络将实现线性卷积。同样，DFT 可以使用两层神经网络计算，每层有 N 个节点。每个输出层节点查找一个频率分量的幅度。这是通过使每个输出层节点的权重与要查找的正弦曲线相同来完成的。生成的网络将输入信号与每个基函数正弦曲线相关联，从而计算DFT。当然，两层神经网络远不如标准的三层架构强大。这意味着神经网络可以执行非线性和线性处理。

假设这些传统 DSP 策略之一用于设计神经网络的权重。可以说网络是最佳的吗？传统的DSP算法通常基于对输入信号特性的假设。例如，假设信号和噪声频谱都是已知的，Wiener滤波是最大化信噪比的最佳方法；相关性对于检测目标（假设噪声为白色）是最佳选择；反卷积抵消了不需要的卷积，假设反卷积核是原始卷积核的反核。

例如，想象一下使用实际输入信号测试传统的 DSP 算法。接下来，使用略微更改的算法重复测试，例如，将其中一个参数增加 1%。如果第二个测试结果优于第一个测试结果，则原始算法不会针对手头的任务进行优化。几乎所有的传统DSP算法都可以通过对算法参数和程序的微小变化进行试错评估来显着改进，这就是神经网络的策略。

4 训练神经网络

神经网络设计可以用一个例子来解释。图 26-8 显示了将要解决的问题，识别文本图像中的单个字母。

开发神经网络的第一步是创建一个示例数据库。对于文本识别问题，这是通过打印 26 个大写字母来实现的：A、B、C、D …Y，Z，在一张纸上 50 次。接下来，这 1300 个字母通过使用可用于个人计算机的众多扫描设备之一转换为数字图像。然后将这个大型数字图像分成 10×10 像素的小图像，每个图像包含一个字母。此信息存储为 1.3 兆字节的数据库：1300 张图像；每张图像 100 像素；每像素 8 位。

将使用该数据库中的前 260 张图像来训练神经网络（即确定权重），其余图像用于测试其性能。数据库还必须包含一种识别每个图像中包含的字母的方法。例如，可以为每个 10×10 的图像添加一个额外的字节，其中包含字母的 ASCII 代码。在另一个方案中，位置数据库中每 10×10 张图像可以指示字母是什么。例如，图像 0 到 49 可能都是“A”，图像 50-99 可能都是“B”，依此类推。

在本演示中，神经网络将设计用于任意任务：确定 10×10 张图像中的哪一张包含元音，即 A、E、I、O 或 U。这可能没有任何实际应用，但它确实说明了神经网络学习非常抽象的模式识别问题的能力。通过在训练集中包含每个字母的十个示例，网络将（希望）学习区分目标图像和非目标图像的关键特征。

本例中使用的神经网络是传统的三层全互连架构，如图 26-5 和 26-6 所示。输入层有 101 个节点（100 个像素值加上一个偏置节点），隐藏层有 10 个节点，输出层有 1 个节点。当将 100 像素的图像应用于网络输入时，如果存在元音，希望输出值接近 1，如果元音不存在，则输出值接近零。不要担心输入信号是以二维数组 （10×10） 的形式获取的，而神经网络的输入是一维数组。这是对像素值如何相互关联的理解；神经网络会找到自己的关系。

表 26-2 显示了用于计算神经网络权重的主程序，表 26-3 包含从主程序调用的三个子程序。数组元素：X1[1] 到 X1[100]，保存输入图层值。此外，X1[101] 始终保持值 1，为偏置节点提供输入。包含隐藏节点的输出值在数组元素中：X2[1] 到 X2[10]。变量 X3 包含网络的输出值。隐藏层的权重包含在数组 WH[,] 中，其中第一个索引标识隐藏节点（1 到 10），第二个索引是输入层节点（1 到 101）。输出层的权重保持在 WO[1] 到 WO[10] 之间。这样一来，总共有 1020 个权重值，用于定义网络的运行方式。

该程序的第一个动作是使用随机数生成器将每个权重设置为任意初始值。如第 190 行至第 240 行所示，隐藏层权重的初始值介于 -0.0005 和 0.0005 之间，而输出层权重介于 -0.5 和 0.5 之间。这些范围被选择为与最终权重必须相同的数量级。这基于：(1)输入信号中的值范围，(2)每个节点处的输入数相加，以及 (3)sigmoid 处于活动状态的值范围，输入约为 -5< x < 5，输出为 0 到 1。例如，当典型值为 100 的 101 个输入乘以典型权重值 0.0002 时，乘积的总和约为 2，在 S 形输入的有效范围内。

如果使用这些随机权重来评估神经网络的性能，我们会期望它与随机猜测相同。学习算法通过在适当的方向上逐渐改变每个权重来提高网络的性能，这称为迭代过程，在程序中由第 270-400 行中的 FOR-NEXT 循环控制。每次迭代都会使权重在将目标示例与非目标示例分开时效率略高。迭代循环通常会一直执行，直到没有进一步的改进。在典型的神经网络中，这可能是一万到一万次迭代，但几百次是很常见的，此示例执行 800 次迭代。

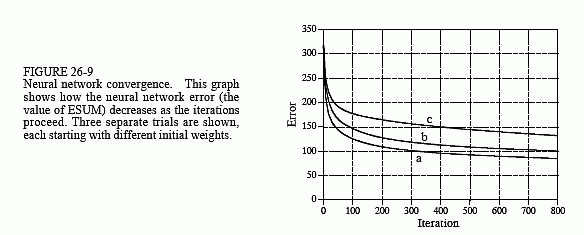
为了使这种迭代策略起作用，必须有一个参数来描述系统当前的性能。变量 ESUM（表示误差和）在程序中提供此功能。迭代循环中的第一个操作是将 ESUM 设置为零（第 290 行），以便它可以用作累加器。在每次迭代结束时，ESUM 的值将打印到视频屏幕（第 380 行），以便操作员可以确保正在取得进展。ESUM 的值将从高开始，并随着神经网络被训练以识别目标而逐渐降低。图 26-9 显示了 ESUM 如何随着迭代的进行而减少的示例。

训练集中的所有 260 张图像在每次迭代期间都会被评估，由第 310-360 行中的 FOR-NEXT 循环控制。子例程1000用于从示例数据库中检索图像。输入子例程 1000 时，参数 LETTER% 介于 1 和 260 之间。返回后，输入节点值 X1[1] 到 X1[100] 包含数据库中与 LETTER% 对应的图像像素值。偏置节点值 X1[101] 始终以常量值 1 返回。子例程 1000 还返回另一个参数 CORRECT。这包含此特定字母的网络所需的输出值。也就是说，如果图像中的字母是元音，则将返回值为 1 的 CORRECT。如果图像中的字母不是元音，则将返回值为零的 CORRECT。

在将正在处理的图像加载到X1[1]到X1[100]之后，子程序2000将数据传递到当前神经网络中以产生输出节点值X3。换言之，子例程2000与表26-1中的程序相同，只是每层中的节点数不同。此子例程还计算当前网络将字母标识为目标或非目标的程度。在第 2210 行中，变量 ELET（表示错误字母）计算为实际生成的输出值 X3 与所需值 CORRECT 之间的差值。这使得 ELET 的值介于 -1 和 1 之间。ELET 的所有 260 个值（第 340 行）被组合在一起形成 ESUM，即整个训练集的网络总平方误差。

第 2220 行显示了计算误差时通常包含的一个选项：为目标和非目标的错误分配不同的重要性。例如，回想一下前面介绍的癌症例子，以及误报误差与假阴性误差的后果。在本例中，将任意声明检测目标的错误是检测非目标错误的五倍。实际上，这告诉网络在目标上做得更好，即使它损害了非目标的性能。

子程序 3000 是神经网络策略的核心，用于在每次迭代中更改权重的算法。当使用进化作为训练算法时，神经网络中的每个权重都会通过添加随机数生成器中的值而略有变化。如果修改后的权重使网络变得更好（即 ESUM 的值较低），则保留更改，否则将丢弃这些更改。虽然这可行，但它的收敛速度非常慢。简单来说，该计划将需要几天时间才能找到解决方案，而不是几分钟或几小时。

之前说过，非线性（sigmoid）需要是可微的。如果知道非线性上每个点的斜率，就可以直接为每个权重的斜率（ΔX3/Δw）写一个方程，而实际上不必扰动它。考虑一个特定的权重，例如 WO[1]，对应于输出节点的第一个输入。看看图 26-5 和 26-6 中的结构，并问：如果这个特定的权重(w)略有变化，但其他一切都保持不变，输出(X3)将受到什么影响？答案是：

其中 $SLOP{E}_O$ 是输出层 sigmoid 的一阶导数，计算了我们在它的曲线上操作的位置。换言之，$SLOP{E}_O$ 描述了 sigmoid 的输出随着 sigmoid 输入的变化而变化的程度。从方程 26-2 中， $SLOP{E}_O$ 可以根据 sigmoid X3 的当前输出值计算得出。此计算显示在第 3160 行中。在第 3170 行中，该权重的斜率通过方程 26-3 计算，并存储在变量 DX3DW（即 ΔX3/Δw）中。

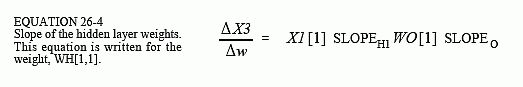
使用类似的分析，可以通过以下方式找到隐藏层上权重的斜率，例如 WH[1,1]：

$SLOP{E}_{H1}$ 是隐层 S 形的一阶导数，我们在它的曲线上进行评估。其他值 X1[1] 和 WO[1] 只是权重变化在进入输出时看到的常量。在第 3070 行和第 3080 行中，使用方程 26-2 计算 S 形曲线的斜率。隐藏层权重 DX3DW 的斜率在第 3090 行中通过方程 26-4 计算。

现在知道了每个权重的斜率，可以看看每个权重在下一次迭代中是如何变化的。通过获取当前权重并添加与斜率成正比的量来找到每个权重的新值：

该计算在隐藏层的第 3100 行和输出层的第 3180 行中执行。比例常数由两个因素组成，ELET（该特定输入的网络误差）和 MU（程序开始时设置的常数）。为了理解此计算中对 ELET 的需求，假设放置在输入端的图像在输出信号中产生一个小误差。接下来，假设应用于输入的另一张图像会产生较大的输出错误。在调整权重时，希望为第二张图像而不是第一张图像推动网络。如果某件事运作不佳，想改变它；如果它运行良好，想不理它。这是通过按当前误差 ELET 的比例更改每个权重来实现的。

在神经网络中，MU 控制每次迭代时权重的变化程度。要使用的值取决于特定问题，低至 10 -6 或高至 0.1。太小的值会导致网络收敛太慢。相比之下，过大的值将导致收敛不稳定，并在最终解周围表现出混沌振荡。不幸的是，神经网络对MU的各种值做出反应的方式可能难以理解或预测。因此，在训练期间监控网络错误（即 ESUM）至关重要，例如在每次迭代结束时将其打印到视频屏幕上。如果系统未正确收敛，请停止程序并尝试 MU 的另一个值。

5 评估结果

那么，它是如何工作的呢？元音识别训练程序运行了三次，使用不同的随机值作为初始权重。在 100 MHz Pentium 人员计算机上完成 800 次迭代大约需要一小时。图 26-9 显示了网络 ESUM 的误差在这段时间内的变化情况。逐渐下降表明网络正在学习任务，并且权重在数百次迭代后达到接近最佳值。每次试验都会产生不同的问题解决方案，最终性能也不同。

在图26-10中，三种解决方案的隐藏层权重显示为图像。这意味着神经网络采取的第一个行动是将这些图像与输入信号相关联（相乘和求和）。它们看起来像随机噪音！这些权重值可以被证明是有效的，但它们为什么有效是一个谜。这里还有一点值得思考。人脑由大约100万亿个神经元组成，每个神经元平均有10,000个互连。如果不能理解这个例子中的简单神经网络，怎么能研究至少复杂 100,000,000,000,000 倍的东西呢？这是21世纪的研究。

图 26-11a 显示了训练集中 260 个字母的神经网络输出的直方图。请记住，选择权重是为了使元音图像的输出接近 1，否则接近零。分离已经完美实现，两个分布之间没有重叠。另请注意，元音分布比非元音分布窄。这是因为声明目标错误的重要性是非目标错误的重要五倍（参见第 2220 行）。

相比之下，图26-11b显示了数据库中图像261至1300的直方图。虽然目标和非目标分布是相当不同的，但它们并不是完全分开的。为什么神经网络在前 260 个字母上的表现比后 1040 个字母更好？图（a）是作弊！换句话说，神经网络识别的是训练集中的特定图像，而不是识别元音和非元音的一般模式。

图 26-12 显示了三种解决方案的性能，显示为 ROC 曲线。试验 （b） 提供的网络明显优于另外两个。这是一个随机机会的问题，具体取决于所使用的初始权重。在一个阈值设置下，试验“b”中设计的神经网络可以检测 25 个目标中的 24 个（即 96% 的元音图像），误报率仅为 25 个非目标中的 1 个（即非元音图像的 4%）。考虑到这个问题的抽象性质，以及所应用的非常通用的解决方案，这还不错。

关于神经网络的一些最后评论。让神经网络在训练期间收敛可能很棘手。如果网络错误（ESUM）没有稳步减少，则必须终止、更改程序，然后重新启动程序。这可能需要多次尝试才能成功。可以改变三件事来影响收敛性：

• （1）MU
• （2）初始随机权重的大小
• （3）隐藏节点的数量（按照它们应该改变的顺序）

神经网络开发中最关键的项目是训练样本的有效性。例如，在开发新的商业产品时，唯一可用的测试数据来自原型、模拟、有根据的猜测等。如果神经网络是根据这些初步信息进行训练的，它可能无法在最终应用程序中正常运行。训练数据库和最终数据之间的任何差异都会降低神经网络的性能（神经网络的墨菲定律）。

6 递归滤波器设计

设计一个递归过滤器，就像设计神经网络一样：从一组通用的递归系数开始，然后使用迭代慢慢地将它们塑造成想要的样子。这种技术很重要，原因有两个：

• 首先，它允许设计自定义递归滤波器，而不必为 z变换 的数学问题而烦恼。
• 其次，它表明传统DSP和神经网络的思想可以结合起来，形成精湛的算法。

此方法的主程序如表 26-4 所示，表 26-5 中有两个子程序。阵列 T[] 保持所需的频率响应，这是手动设计的某种曲线。由于该程序基于FFT，因此信号的长度必须为2的幂。如前所述，该程序使用 FFT 长度 256，由第 130 行中的变量 N% 定义。这意味着 T[0] 到 T[128] 对应于采样率的 0 到 0.5 之间的频率。此数组中仅包含幅度；在这个设计中，相位不受控制。

递归系数在第 270-310 行中设置为其初始值，通常选择为恒等系。不要在这里使用随机数，否则初始过滤器将不稳定。递归系数保存在数组 A[] 和 B[] 中。变量 NP% 设置所设计滤波器中的极点数。例如，如果 NP% 为 5，则“a”系数从 A[0] 到 A[5]，而“b”系数从 B[1] 到 B[5]。

如前所述，迭代过程需要一个值来描述当前系统的运行情况。这由变量 ER（表示误差）提供，并在子例程 3000 中计算。行 3040 到 3080 在阵列 IMX[] 中加载一个脉冲。接下来，第 3100-3150 行使用此脉冲作为递归滤波器的输入信号，该信号由 A[] 和 B[] 的电流值定义。因此，该滤波器的输出是当前系统的脉冲响应，并存储在阵列 REX[] 中。然后通过获取脉冲响应的FFT来找到系统的频率响应，如第3170行所示。子程序 1000 是第 12 章表 12-4 中列出的 FFT 程序。此 FFT 子例程以矩形形式返回频率响应，覆盖数组 REX[] 和 IMX[]。

然后，第 3200-3250 行计算 ER，即当前频率响应幅度与所需频率响应之间的均方误差。该程序的迭代操作优化了此错误，使其定义方式非常重要。FOR-NEXT环路贯穿频率响应中的每个频率。对于每个频率，行 3220 根据矩形数据计算当前频率响应的幅度。在第 3230 行中，通过从当前幅度 MAG 中减去所需的幅度 T[] 来发现该频率的误差。然后将此误差平方，并添加到累加器变量 ER 中。在遍历每个频率后，线路 3250 完成计算，使 ER 成为整个频率响应的均方误差。

第 340 行到第 380 行控制程序的迭代循环。子例程 2000 是对递归系数进行更改的地方。该子例程中的第一个操作是确定 ER 的当前值，并将其存储在另一个变量 EOLD 中（第 2040 行和第 2050 行）。子例程更新系数后，将再次确定 ER 的值，并将其分配给变量 ENEW（第 2270 行和第 2280 行）。

变量 MU 控制迭代步长，就像在前面的神经网络程序中一样。该程序中使用了一项高级功能：自动调整MU的值。这就是拥有 EOLD 和 ENEW 这两个变量的原因。当程序启动时，MU 设置为相对较高的值 0.2（第 160 行）。这允许收敛快速进行，但会限制滤波器与最佳解的接近程度。随着迭代的进行，将达到没有进展的点，ENEW 比 EOLD 高。每次发生这种情况时，第 370 行都会减少 MU 的值。

子程序 2000 根据最陡峭的体面方法更新递归系数：计算每个系数的斜率，然后将系数更改与其斜率成正比的量。第 2080-2130 行计算 “a” 系数的斜率，并将它们存储在数组 SA[] 中。同样，第 2150-2200 行计算 “b” 系数的斜率，将它们存储在数组 SB[] 中。然后，第 2220-2250 行将每个递归系数修改为与这些斜率成比例的量。在这个程序中，比例常数就是步长 MU。比例常数中不需要误差项，因为只有一个示例需要匹配：所需的频率响应。

最后一个问题是程序如何计算递归系数的斜率。在神经网络示例中，推导了斜率方程。此处不能使用此过程，因为它需要将导数跨过 DFT。取而代之的是，应用了一种蛮力方法：实际以很小的增量改变递归系数，然后直接计算ER的新值。然后，斜率为ER的变化除以增量。具体而言，ER 的当前值位于第 2040-2050 行中，并存储在变量 EOLD 中。第 2080-2130 行中的循环贯穿每个“a”系数。此循环中的第一个操作是向正在处理的递归系数（第 2090 行）添加一个小增量 DELTA。子例程 3000 在第 2100 行中调用，以查找具有修改系数的 ER 值。然后，第 2110 行将该系数的斜率计算为：（ER - EOLD）/DELTA。然后，第 2120 行通过减去 DELTA 的值来恢复修改后的系数。

图 26-13 显示了使用此程序设计的过滤器的几个示例。虚线是所需的频率响应，而实线是所设计滤波器的频率响应。这些滤波器中的每一个都需要几分钟才能汇聚到 100 MHz Pentium 上。图（a）是一个8极点低通滤波器，其中误差在整个频谱（所写的程序）上均等加权。图（b）是相同的滤波器，只是在计算ER时阻带中的误差乘以8。这迫使滤波器具有较小的阻带纹波，但代价是通带中的纹波更大。

图（c）显示了 1/sinc（x） 的 2 极滤波器。此筛选器中的误差仅在 0 和 0.45 之间求和，从而在此范围内产生更好的匹配，但代价是 0.45 和 0.5 之间的匹配较差。最后，（d）是一个非常不规则的6极频率响应，包括急剧下降。为了实现收敛，递归系数最初被设置为notch滤波器的递归系数。