蓝桥杯每日一题----单调栈和单调队列
单调栈和单调队列
单调栈
单调栈即栈内的元素是单调递减或者单调递增的,我们通过一个题目来理解。
单调栈模板题
题目描述
给出项数为 n 的整数数列 a 1 … a n a_1…a_n a1…an。
定义函数 f ( i ) f(i) f(i)代表数列中第 i 个元素之后第一个大于 a i a_i ai 的元素的下标,即 f ( i ) = m i n i < j < = n , a j > a i j f(i)=min_{i
试求出 f ( 1 … n ) f(1…n) f(1…n)。
输入格式
第一行一个正整数 n。
第二行 n 个正整数 a 1 … a n a_1…a_n a1…an。
输出格式
一行n个整数表示 f ( 1 ) , f ( 2 ) , … , f ( n ) f(1),f(2),…,f(n) f(1),f(2),…,f(n)的值。
题目分析
题目要求第i个数后面第一个比 a [ i ] a[i] a[i]大的数。首先从头遍历数组,将第一个元素入栈,接着遍历下一个元素,假设当前入栈的元素下标为i,当前遍历到了 i + 1 i+1 i+1,如果 a [ i ] > a [ i + 1 ] a[i]>a[i+1] a[i]>a[i+1],那么 a [ i + 1 ] a[i+1] a[i+1]就不入栈接着向后遍历,如果 a [ i ] < a i + 1 a[i]
换个思路,假设我们是找 i i i左边第一个比 i i i小的数字,从头开始遍历数组,将第一个元素入栈,接着遍历下一个元素,假设当前入栈的元素下标为 i i i,当前遍历到了 i + 1 i+1 i+1,如果 a [ i + 1 ] > = a [ i ] a[i+1]>=a[i] a[i+1]>=a[i],则将 a [ i ] a[i] a[i]从栈中弹出,因为 a [ i + 1 ] a[i+1] a[i+1]在 a [ i ] a[i] a[i]的右边,对于求左边第一个比 a [ i + 2 ] a[i+2] a[i+2]大的数字,如果 a [ i ] > a [ i + 2 ] a[i]>a[i+2] a[i]>a[i+2],必然会有 a [ i + 1 ] > a [ i + 2 ] a[i+1]>a[i+2] a[i+1]>a[i+2],而 a [ i + 1 ] a[i+1] a[i+1]从左边更靠近 a [ i + 2 ] a[i+2] a[i+2],所以它会成为答案,也就是只要 a [ i + 1 ] a[i+1] a[i+1]在这里, a [ i ] a[i] a[i]永远不会成为答案,所以直接弹出就行了。那么最后栈顶的元素要么为空要么大于 a [ i + 1 ] a[i+1] a[i+1],并且是从 a [ i + 1 ] a[i+1] a[i+1]往左数第一个大于 a [ i + 1 ] a[i+1] a[i+1]的数字,所以栈顶元素即为我们想要的答案。
上述思路用一个图来表示,1,2,3,4,5表示的是数组下标,矩形的高度表示的是数组中值的大小,值越大,矩形越高。
当遍历到3的时候,2比3小,所以要从栈里面弹出,后续遍历到4,即便2要比4大,但是因为3的存在只要2符合条件3一定符合条件,但是3要比2更靠近4,也就是更靠近后面的数,所以3永远不会成为答案,把3弹出栈没有问题。遍历到5的时候,虽然3要比4大,也比5大,但是4比5大且更靠近5,所以4是答案。而如果5大于4小于3时,3又会成为答案,所以此时无论是4还是3都有可能成为答案,所以他们留在栈中。
换个形象点的方式,就是站在4上向左看,比3小的数字一定会被3挡住,所以从栈中拿掉就可以了,比如站在4中向左看,只能看到1和3,此时栈中也就只剩下了1和3。站在5中向左看,可以看见1,3,4。
刚刚讲的是求一个数字左边第一小的数字,但是题目要求的是右边第一小的数字,那么只需要对原数组倒序遍历就是求左边第一小的数字了。
题目代码
package 单调队列和单调栈;
import java.util.Scanner;
import java.util.Stack;
public class 单调栈模板 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int a[] = new int[n+1];
int f[] = new int[n+1];
for(int i = 1;i <= n;i++) a[i] = scanner.nextInt();
Stack<Integer> stack = new Stack<Integer>();
for(int i = n;i > 0;i--) {
while(!stack.isEmpty()&&a[stack.peek()]<=a[i]) stack.pop();
if(!stack.isEmpty())
f[i] = stack.peek();
stack.push(i);
}
for(int i = 1;i <= n;i++)
System.out.print(f[i] + " ");
}
}
ps:感觉洛谷对非c++不太友好,很容易超时或者超内存,这个代码就有几个样例超内存了。
单调队列实现滑动窗口
单调栈值从栈顶弹元素和进元素,单调队列从队头弹元素,从队尾进元素。
单调队列模板
题目描述
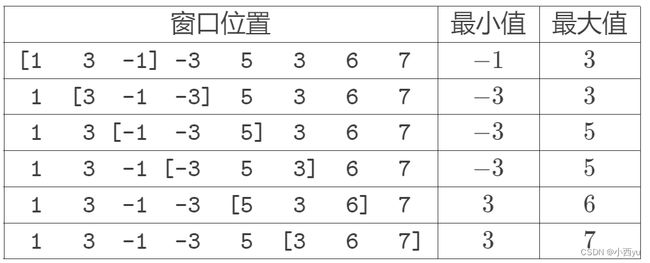
有一个长为 n 的序列 a,以及一个大小为 k 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如,对于序列 [ 1 , 3 , − 1 , − 3 , 5 , 3 , 6 , 7 ] [1,3,−1,−3,5,3,6,7] [1,3,−1,−3,5,3,6,7]以及 k=3,有如下过程:
输入格式
输入一共有两行,第一行有两个正整数 n,k。 第二行 n 个整数,表示序列 a
输出格式
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
题目分析
用队列来模拟一下滑动窗口的过程。两个判断
第一个判断是否还在窗口内,因为随着窗口的滑动必然会有一些数字已经离开了窗口,这个时候就要从队列里面删掉。
第二个判断是否有无效数字。对于求最大值的队列来说,假设窗口内的数字是[1,2,1],那么第一个数字1可以提早删掉,因为此时的2是窗口内的最大值并且只要第一个1没有被移出窗口那么2必然也还在,也就是第一个1受2的“压制”永远不会成为窗口内的最大值,直接删掉就可以了。变成了[2,1],那么此时剩下的这个1需要删掉吗?不能删掉,因为数字2会比1先离开窗口,当2离开窗口后,1仍然有机会成为最大值。也就是说这里存的应该是一个单调递减序列,当前待入队数字比队尾数字大,队尾数字就出队。
那么最大值在哪?单调递减序列,最大值自然是第一个数字也就是队头元素。
同样队列里面存的是数组的下标,因为我可以通过数组下标快速判断数字是否还在窗口内,假设当前数字下标为5,窗口大小为3,那么下标小于等于5-3=2的直接出队。
求最小值也是同样的分析方式。
题目代码
package 单调队列和单调栈;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Scanner;
public class 单调队列模板 {
public static void main(String[] args) throws IOException {
Scanner scanner = new Scanner(System.in);
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] strings = br.readLine().split(" ");
int n = Integer.parseInt(strings[0]);
int k = Integer.parseInt(strings[1]);
int a[] = new int[n+1];
int max[] = new int[n+1];
int min[] = new int[n+1];
strings = br.readLine().split(" ");
for(int i = 1;i <= n;i++) a[i] = Integer.parseInt(strings[i-1]);
Deque<Integer> qDeque = new ArrayDeque<Integer>();
for(int i = 1;i <= n;i++) {
while(!qDeque.isEmpty()&&i-qDeque.peekFirst()>=k) {
qDeque.pollFirst();
}
while(!qDeque.isEmpty()&&a[qDeque.peekLast()]<=a[i]) {
qDeque.pollLast();
}
qDeque.addLast(i);
max[i] = a[qDeque.peekFirst()];
}
qDeque.clear();
for(int i = 1;i <= n;i++) {
while(!qDeque.isEmpty()&&i-qDeque.peekFirst()>=k) qDeque.pollFirst();
while(!qDeque.isEmpty()&&a[qDeque.peekLast()]>=a[i]) qDeque.pollLast();
qDeque.addLast(i);
if(i>=k)
min[i] = a[qDeque.peekFirst()];
}
for(int i = k;i <= n;i++)
System.out.print(min[i] + " ");
System.out.println();
for(int i = k;i <= n;i++)
System.out.print(max[i] + " ");
}
}
ps:洛谷提交会超时