C#,二叉搜索树(Binary Search Tree)的迭代方法与源代码
1 二叉搜索树
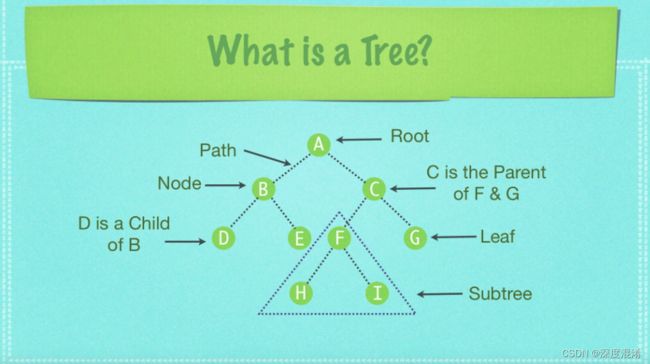
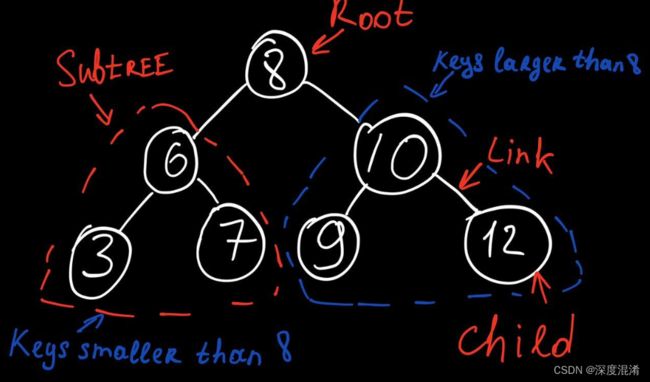
二叉搜索树(BST,Binary Search Tree)又称二叉查找树或二叉排序树。
一棵二叉搜索树是以二叉树来组织的,可以使用一个链表数据结构来表示,其中每一个结点就是一个对象。
一般地,除了key和位置数据之外,每个结点还包含属性Left、Right和Parent,分别指向结点的左、右子节点和父结点。
如果某个子结点或父结点不存在,则相应属性的值为空(null)。
根结点是树中唯一父指针为null的结点。
叶子结点的孩子结点指针也为null。
2 节点数据定义
///
/// 二叉树的节点类
///
public class BinaryNode
{
///
/// 名称
///
public string Name { get; set; } = "";
///
/// 数据
///
public string Data { get; set; } = "";
///
/// 左节点
///
public BinaryNode Left { get; set; } = null;
///
/// 右节点
///
public BinaryNode Right { get; set; } = null;
///
/// 构造函数
///
public BinaryNode()
{
}
///
/// 单数值构造函数
///
///
public BinaryNode(string d)
{
Name = d;
Data = d;
}
public BinaryNode(int d)
{
Name = d + "";
Data = d + "";
}
///
/// 构造函数
///
///
///
public BinaryNode(string n, string d)
{
Name = n;
Data = d;
}
///
/// 返回邻接的三元组数据
///
///
public string[] ToAdjacency()
{
string adj = "";
if (Left != null)
{
adj += Left.Name;
}
if (Right != null)
{
if (adj.Length > 0) adj += ",";
adj += Right.Name;
}
return new string[] { Name, Data, adj };
}
///
/// 邻接表
///
///
public List
{
return new List
}
public int Key
{
get
{
return Int32.Parse(Data);
}
set
{
Data = value.ToString();
}
}
}
///
/// 二叉树的节点类
///
public class BinaryNode
{
///
/// 名称
///
public string Name { get; set; } = "";
///
/// 数据
///
public string Data { get; set; } = "";
///
/// 左节点
///
public BinaryNode Left { get; set; } = null;
///
/// 右节点
///
public BinaryNode Right { get; set; } = null;
///
/// 构造函数
///
public BinaryNode()
{
}
///
/// 单数值构造函数
///
///
public BinaryNode(string d)
{
Name = d;
Data = d;
}
public BinaryNode(int d)
{
Name = d + "";
Data = d + "";
}
///
/// 构造函数
///
///
///
public BinaryNode(string n, string d)
{
Name = n;
Data = d;
}
///
/// 返回邻接的三元组数据
///
///
/// 邻接表
///
/// ToList()
{
return new List(ToAdjacency());
}
public int Key
{
get
{
return Int32.Parse(Data);
}
set
{
Data = value.ToString();
}
}
}
3 二叉树的节点插入与搜索与验证代码
using System;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
///
/// BST(二叉搜索树的迭代方法)
///
public static partial class Algorithm_Gallery
{
public static BinaryNode Insert(BinaryNode node, int key)
{
if (node == null)
{
return new BinaryNode(key);
}
if (key < node.Key)
{
node.Left = Insert(node.Left, key);
}
else if (key > node.Key)
{
node.Right = Insert(node.Right, key);
}
return node;
}
public static int BST_Find_Floor(BinaryNode root, int key)
{
BinaryNode curr = root;
BinaryNode ans = null;
while (curr != null)
{
if (curr.Key <= key)
{
ans = curr;
curr = curr.Right;
}
else
{
curr = curr.Left;
}
}
if (ans != null)
{
return ans.Key;
}
return -1;
}
public static int BST_Drive()
{
int N = 25;
BinaryNode root = new BinaryNode("19");
Insert(root, 2);
Insert(root, 1);
Insert(root, 3);
Insert(root, 12);
Insert(root, 9);
Insert(root, 21);
Insert(root, 19);
Insert(root, 25);
return BST_Find_Floor(root, N);
}
}
}
POWER BY TRUFFER.CN
BY 315SOFT.COM
using System;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
///
/// BST(二叉搜索树的迭代方法)
///
public static partial class Algorithm_Gallery
{
public static BinaryNode Insert(BinaryNode node, int key)
{
if (node == null)
{
return new BinaryNode(key);
}
if (key < node.Key)
{
node.Left = Insert(node.Left, key);
}
else if (key > node.Key)
{
node.Right = Insert(node.Right, key);
}
return node;
}
public static int BST_Find_Floor(BinaryNode root, int key)
{
BinaryNode curr = root;
BinaryNode ans = null;
while (curr != null)
{
if (curr.Key <= key)
{
ans = curr;
curr = curr.Right;
}
else
{
curr = curr.Left;
}
}
if (ans != null)
{
return ans.Key;
}
return -1;
}
public static int BST_Drive()
{
int N = 25;
BinaryNode root = new BinaryNode("19");
Insert(root, 2);
Insert(root, 1);
Insert(root, 3);
Insert(root, 12);
Insert(root, 9);
Insert(root, 21);
Insert(root, 19);
Insert(root, 25);
return BST_Find_Floor(root, N);
}
}
}