算法沉淀——多源 BFS(leetcode真题剖析)
算法沉淀——多源 BFS(leetcode真题剖析)
- 01.矩阵
- 02.飞地的数量
- 03.地图中的最高点
- 04.地图分析
多源
BFS 是指从多个源点同时进行广度优先搜索的算法。在传统的 BFS 中,我们通常从一个起始点开始,逐层遍历所有的相邻节点。而在多源 BFS 中,我们可以同时从多个源点开始,从这些源点出发,逐层向外扩展,直到达到目标或者遍历完整个图。
多源 BFS 可以用于解决一些问题,例如:
- 多个人同时逃生: 在一个迷宫中,有多个人同时被困在不同的位置,需要找到最短路径逃离迷宫。可以从这些人的位置同时开始
BFS,第一个相遇的点就是大家逃生的最短路径。 - 多点到达目标问题: 在一些网络传播或者路由问题中,多个点需要同时到达某个目标点,可以使用多源
BFS找到最短路径。 - 并行计算: 在一些并行计算的场景中,多源
BFS可以用于并行地计算多个点到其他点的最短路径。
多源 BFS 的实现方式与单源 BFS 类似,只是需要同时从多个源点开始扩展。通常使用队列来进行层次遍历,每一层表示到达目标的步数。
01.矩阵
题目链接:https://leetcode.cn/problems/01-matrix/
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
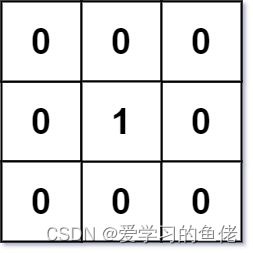
输入:mat = [[0,0,0],[0,1,0],[0,0,0]]
输出:[[0,0,0],[0,1,0],[0,0,0]]
输入:mat = [[0,0,0],[0,1,0],[1,1,1]]
输出:[[0,0,0],[0,1,0],[1,2,1]]
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j] is either 0 or 1.mat中至少有一个0
思路
从 0 开始层序遍历,并且记录遍历的层数。当第一次碰到 1 的时候,当前的层数就是这个 1 离 0 的最短距离。这一种方式,在遍历的时候标记一下处理过的 1 ,能够做到只用遍历整个矩阵一次,就能得到最终结果。但是,这里有一个问题, 0 是有很多个的,我们怎么才能保证遇到的 1 距离这一个 0 是最近的呢? 其实很简单,我们可以先把所有的 0 都放在队列中,把它们当成一个整体,每次把当前队列里面的所有元素向外扩展一次。
代码
class Solution{
const int dx[4]={0,0,1,-1};
const int dy[4]={-1,1,0,0};
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int m=mat.size(),n=mat[0].size();
vector<vector<int>> dist(m,vector<int>(n,-1));
queue<pair<int,int>> q;
for(int i=0;i<m;++i)
for(int j=0;j<n;++j)
if(mat[i][j]==0){
q.push({i,j});
dist[i][j]=0;
}
while(!q.empty()){
auto [a,b]=q.front();
q.pop();
for(int i=0;i<4;++i){
int x=a+dx[i],y=b+dy[i];
if(x>=0&&x<m&&y>=0&&y<n&&dist[x][y]==-1){
dist[x][y]=dist[a][b]+1;
q.push({x,y});
}
}
}
return dist;
}
};
02.飞地的数量
题目链接:https://leetcode.cn/problems/number-of-enclaves/
给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边界。
返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
输入:grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出:3
解释:有三个 1 被 0 包围。一个 1 没有被包围,因为它在边界上。
输入:grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出:0
解释:所有 1 都在边界上或可以到达边界。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 500grid[i][j]的值为0或1
思路1
中间的1要达到边界,首先就是要有1在边界并且能够接触到,所以我们可以直接在周围一圈做单源BFS遍历1,将它改为0,再遍历整个数组,剩下的1就是出不去的。
代码1
class Solution {
const int dx[4]={0,0,1,-1};
const int dy[4]={-1,1,0,0};
int m,n;
queue<pair<int,int>> q;
void bfs(vector<vector<int>>& grid,int i,int j){
q.push({i,j});
grid[i][j]=0;
while(!q.empty()){
int sz=q.size();
while(sz--){
auto [a,b]=q.front();
q.pop();
for(int k=0;k<4;++k){
int x=a+dx[k],y=b+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1){
grid[x][y]=0;
q.push({x,y});
}
}
}
}
}
public:
int numEnclaves(vector<vector<int>>& grid) {
m=grid.size(),n=grid[0].size();
for(int i=0;i<m;++i){
if(grid[i][0]==1) bfs(grid,i,0);
if(grid[i][n-1]==1) bfs(grid,i,n-1);
}
for(int i=1;i<n-1;++i){
if(grid[0][i]==1) bfs(grid,0,i);
if(grid[m-1][i]==1) bfs(grid,m-1,i);
}
int ret=0;
for(int i=0;i<m;++i)
for(int j=0;j<n;++j)
if(grid[i][j]==1) ret+=1;
return ret;
}
};
思路2
使用多源BFS同时对周边的1进行遍历
代码2
class Solution {
// 定义四个方向的坐标变化
const int dx[4] = {0, 0, 1, -1};
const int dy[4] = {1, -1, 0, 0};
public:
int numEnclaves(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
// 用于标记是否访问过的二维布尔型数组
vector<vector<bool>> vis(m, vector<bool>(n));
// 广度优先搜索的队列
queue<pair<int, int>> q;
// 1. 把边上的 1 加入到队列中
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (i == 0 || i == m - 1 || j == 0 || j == n - 1)
if (grid[i][j] == 1) {
q.push({i, j});
vis[i][j] = true;
}
// 2. 多源 BFS
while (!q.empty()) {
auto [a, b] = q.front();
q.pop();
for (int i = 0; i < 4; i++) {
int x = a + dx[i], y = b + dy[i];
// 如果相邻单元格是陆地且未访问过,加入队列并标记为已访问
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && !vis[x][y]) {
vis[x][y] = true;
q.push({x, y});
}
}
}
// 3. 统计结果
int ret = 0;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
// 统计未被包围的陆地单元格数量
if (grid[i][j] == 1 && !vis[i][j])
ret++;
return ret;
}
};
03.地图中的最高点
题目链接:https://leetcode.cn/problems/map-of-highest-peak/
给你一个大小为 m x n 的整数矩阵 isWater ,它代表了一个由 陆地 和 水域 单元格组成的地图。
- 如果
isWater[i][j] == 0,格子(i, j)是一个 陆地 格子。 - 如果
isWater[i][j] == 1,格子(i, j)是一个 水域 格子。
你需要按照如下规则给每个单元格安排高度:
- 每个格子的高度都必须是非负的。
- 如果一个格子是 水域 ,那么它的高度必须为
0。 - 任意相邻的格子高度差 至多 为
1。当两个格子在正东、南、西、北方向上相互紧挨着,就称它们为相邻的格子。(也就是说它们有一条公共边)
找到一种安排高度的方案,使得矩阵中的最高高度值 最大 。
请你返回一个大小为 m x n 的整数矩阵 height ,其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法,请返回 任意一个 。
示例 1:
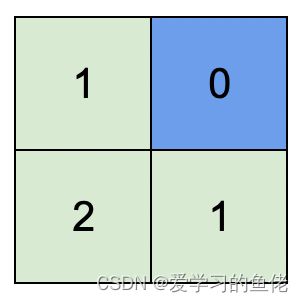
输入:isWater = [[0,1],[0,0]]
输出:[[1,0],[2,1]]
解释:上图展示了给各个格子安排的高度。
蓝色格子是水域格,绿色格子是陆地格。
示例 2:
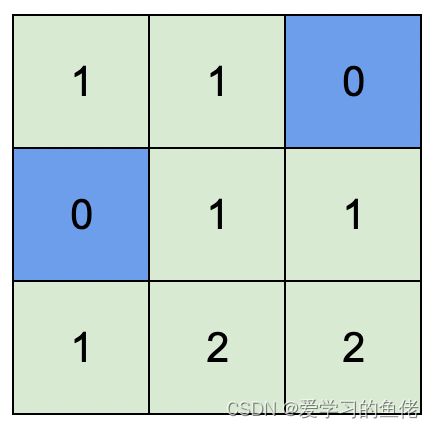
输入:isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出:[[1,1,0],[0,1,1],[1,2,2]]
解释:所有安排方案中,最高可行高度为 2 。
任意安排方案中,只要最高高度为 2 且符合上述规则的,都为可行方案。
思路
这一题我们要读懂题意,将原数组画出就不难发现其实和第一题矩阵的解法是一样的,同样都是使用多源BFS来解决这个问题
代码
class Solution {
const int dx[4] = {0, 0, 1, -1};
const int dy[4] = {-1, 1, 0, 0};
public:
vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
int m = isWater.size(), n = isWater[0].size();
vector<vector<int>> dist(m, vector<int>(n, -1));
queue<pair<int, int>> q;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (isWater[i][j]) {
dist[i][j] = 0;
q.push({i, j});
}
while (!q.empty()) {
auto [a, b] = q.front();
q.pop();
for (int i = 0; i < 4; ++i) {
int x = a + dx[i], y = b + dy[i];
if (x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1) {
dist[x][y] = dist[a][b] + 1;
q.push({x, y});
}
}
}
return dist;
}
};
- 创建一个二维矩阵
dist,用于存储每个位置到水域的最近距离。初始化所有元素为-1。 - 创建一个队列
q,用于进行广度优先搜索。将所有水域的位置(isWater[i][j]为1的位置)加入队列,并将其到水域的距离设为0。 - 使用
BFS遍历队列,不断扩展到达的位置。对于每个位置,检查其四个相邻的位置,如果相邻位置合法且未被访问过,更新其到水域的距离并将该位置加入队列。 - 最终,返回计算得到的
dist矩阵。
04.地图分析
题目链接:https://leetcode.cn/problems/as-far-from-land-as-possible/
你现在手里有一份大小为 n x n 的 网格 grid,上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地。
请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的,并返回该距离。如果网格上只有陆地或者海洋,请返回 -1。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。
示例 1:
输入:grid = [[1,0,1],[0,0,0],[1,0,1]]
输出:2
解释:
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大,最大距离为 2。
示例 2:
输入:grid = [[1,0,0],[0,0,0],[0,0,0]]
输出:4
解释:
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大,最大距离为 4。
提示:
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j]不是0就是1
思路
我们可以将每个陆地同时向海洋扩张,更新海洋到陆地的距离,最终更新的数组中最大的那个数就是最大距离,问题转化后看似是找最大距离,其实找的是最近距离,和第一题矩阵有异曲同工之妙。
代码
class Solution {
const int dx[4]={0,0,1,-1};
const int dy[4]={-1,1,0,0};
public:
int maxDistance(vector<vector<int>>& grid) {
int m=grid.size(),n=grid[0].size();
vector<vector<int>> dist(m,vector<int>(n,-1));
queue<pair<int,int>> q;
for(int i=0;i<m;++i)
for(int j=0;j<n;++j)
if(grid[i][j]){
dist[i][j]=0;
q.push({i,j});
}
int ret=-1;
while(!q.empty()){
auto [a,b] = q.front();
q.pop();
for(int i=0;i<4;i++){
int x=a+dx[i],y=b+dy[i];
if(x>=0&&x<m&&y>=0&&y<n&&dist[x][y]==-1){
dist[x][y]=dist[a][b]+1;
q.push({x,y});
ret=max(ret,dist[x][y]);
}
}
}
return ret;
}
};