算法学习笔记 4-3 深搜(DFS)与广搜(BFS):初识问题状态空间 与 LeetCode真题(Java)
喜欢该类型文章可以给博主点个关注,博主会持续输出此类型的文章,知识点很全面,再加上LeetCode的真题练习,每一个LeetCode题解我都写了详细注释,比较适合新手入门数据结构与算法,后续也会更新进阶的文章。
课件参考—开课吧《门徒计划》
4-3 深搜(DFS)与广搜(BFS):初识问题状态空间
搜索的核心概念
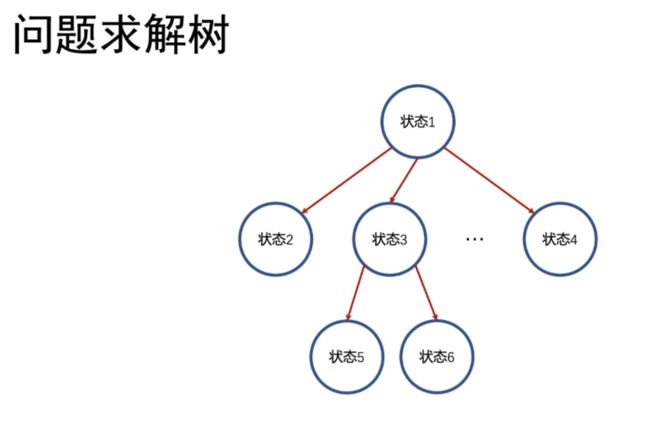
首先给大家拓展一个概念,这个概念就是我们学习搜索算法中非常重要的一环:
这个问题求解树是一个抽象的概念,是在我们自己脑海中根据问题所展开的一个树,也叫递归搜索树,状态展开树。
现在大家对这个树肯定还是一片朦胧,我们根据具体的例子来讲解一下:
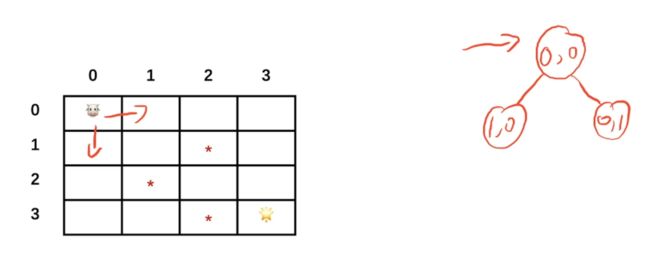
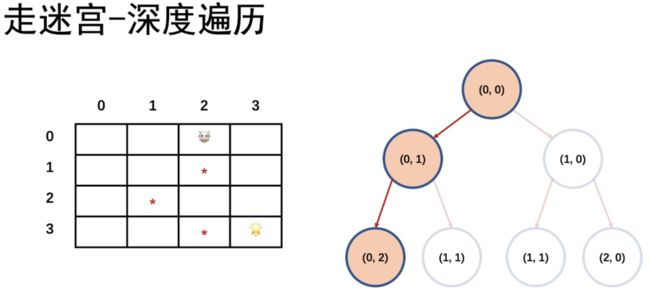
在 ( 0 , 0 ) (0, 0) (0,0)点有一头,它需要找到在 ( 3 , 3 ) (3, 3) (3,3)的⭐️,* 是障碍物。
怎么根据这个走迷宫对应我们的问题求解树呢?我们的初始状态1就是所在的坐标,可以往下走或者往右走,往下走坐标变为 ( 1 , 0 ) (1, 0) (1,0),往右走坐标变为 ( 0 , 1 ) (0, 1) (0,1):
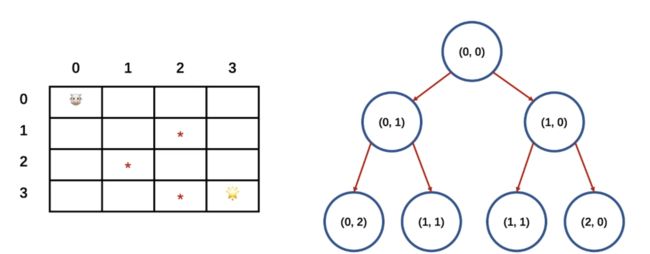
再展开一部分:
这样逐步的展开,我们一定能寻找到 ( 3 , 3 ) (3, 3) (3,3)⭐️的位置。
如果走迷宫你不会走,那我们就把问题转换成在二叉树上的遍历问题。
什么是深搜和广搜?
我们深搜和广搜分别代表着我们遍历问题求解树不同的形式。
什么是搜索剪枝和优化?
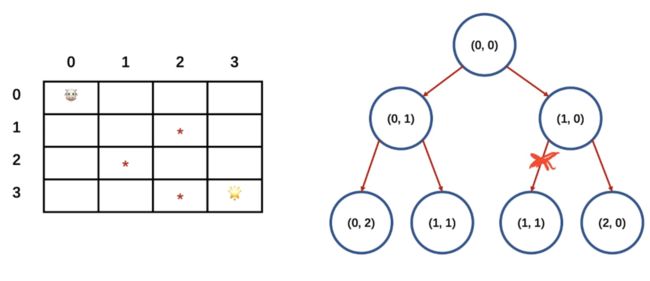
我们把多余的树枝剪掉,此时 ( 1 , 1 ) (1,1) (1,1)这个点无论是往下走还是往右走都会遇到 *,所以我们可以直接将 ( 1 , 1 ) (1,1) (1,1)这个分支去掉,就做到了优化。
设计搜索算法的核心关键点是什么?
搜索算法最核心的问题:设计我们问题求解树当中节点的状态。
因为我们搜索就是相当于在整个问题求解树中遍历。
我们如何设计问题求解树中每一个节点代表的意义,就是我们搜索算法的核心关键点。
DFS — 深度优先搜索
我们从起点开始搜索,直到搜索到边界我们再返回到上一节点:
此时回到 ( 0 , 1 ) (0,1) (0,1)节点,又搜索到了 ( 1 , 1 ) (1,1) (1,1)节点:
( 1 , 1 ) (1,1) (1,1)节点也是边界了,此时我们左子树已全部搜索,所以我们返回到起点,开始搜索右子树,与搜索左子树同理。
其实我们发现,深度优先搜索就是我们二叉树的中序遍历。
先找到一条路,一搜到底,走到头了我们再回来,继续搜索。
DFS总结
递归就是深度优先搜索(DFS)。
BFS — 广度优先搜索
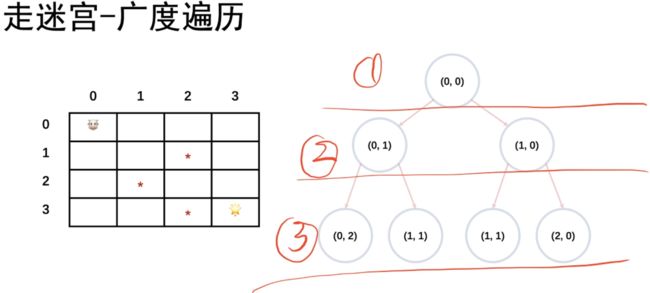
以层序遍历的方式进行遍历,把树分层,按层搜索,先搜索第一层,再搜索第二层…
我们从起点开始搜,从第一层搜到第二层:
由第二层的节点扩展搜索到第三层:
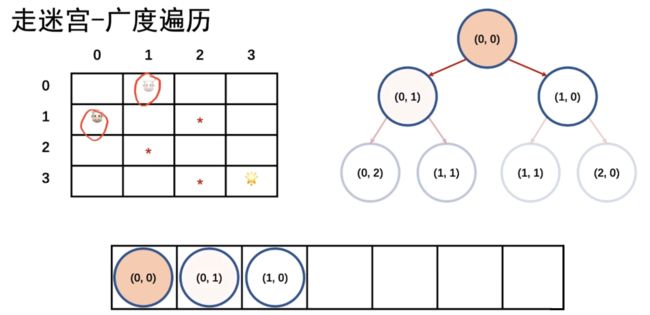
那么广搜我们怎么实现呢?我们知道,深搜用的是递归,借助的是系统栈,广搜其实是借助我们的队列。
先将第一层的入队,然后找到第二层的所有节点,将第一层的节点出队,随后将第二层的节点全部入队,以此类推。
我们可以发现,这个节点在第几层,就代表着我走几步能走到这个节点。
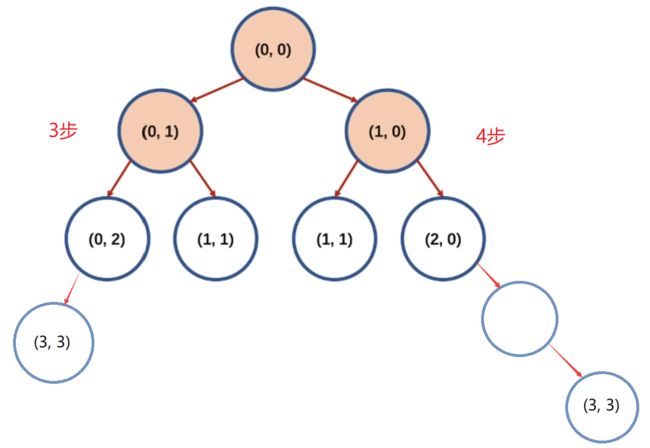
但我们这样搜索,很大的概率会有重复的值,那我们可以做一个这样的假设,我们要寻找到 ( 3 , 3 ) (3,3) (3,3)这个点:
我们走左子树需要3步,走右子树需要4步,当我们要求到点 ( 3 , 3 ) (3,3) (3,3)的最短路径时,我们广度优先搜索的优势就体现出来了,当我们第一次遍历到结果时,那答案必然就是最短路径。
所以我们经常使用广度优先搜索求最优解的问题。
BFS总结
搜索总结
区分DFS与BFS
此时大家可能还会觉得有点抽象,我们举一个具体的例子利用代码来分析:
DFS,关注圈红代码区域,是代码的不同点。
BFS,每一个颜色都是一层。
剪枝
其实我们的代码中就有剪枝:
一些更细节的剪枝:
具体的例子剪枝:
对于具体问题的特判,就是剪枝。
以上都是显示图的搜索,那接下来我们看看隐式图的搜索:
一看是最小步数,那我们肯定优先想到bfs。
广搜就是从根节点开始往下找,找到一个最近的、符合条件的一个点。
BFS、双向BFS、A*启发式搜索
双向BFS也比较少见,但它会使我们搜索的面积变小,对于某些题还是非常合适的。
这里只是简单介绍一下A*搜索,一般情况下是遇不到的,只有在项目里有特殊需求,或者ACM竞赛才会遇到。
估价函数:把所有的下一个可能进行排序,选一个权值最小的点作为下一步,它没有走多余的步骤。
经过上图 想必大家的理解会更清晰了。
LeetCode真题
DFS
LeetCode130. 被围绕的区域
难度:mid
在一个矩阵中,把所有被'X'围起来的'O'变为'X',那么最外层的'O'一定不会变为'X',同时与最外层的'O'相邻的也不会变为'X'。
我们可以把这些'O'标记成别的符号,例如'#',再遍历一遍矩阵把剩下的'O'变为'X',最后把'#'还原为'O'即可。
LeetCode题解:代码实现
LeetCode494. 目标和
难度:mid
对于三个数 A B C ABC ABC,我们可以得到这样的一棵树:
我们可以dfs遍历所有情况,用 t a r g e t + n u m s [ i ] target + nums[i] target+nums[i] 或者 t a r g e t − n u m s [ i ] target - nums[i] target−nums[i] 来判断拼凑出来的每个方案的值是否为 0 0 0,如果为 0 0 0 则说明找到了一种答案,把所有方案数相加即可。
LeetCode题解:代码实现
LeetCode473. 火柴拼正方形
难度:mid
给我们若干个火柴的长度,把它们拼成一个正方形,且每个火柴都必须使用一次。
如果这些火柴能拼成正方形,那它们的总长度 s u m sum sum 肯定可以被 4 4 4 整除。
把所有火柴分成 4 4 4 份,且每份的长度都相等 ( s u m / 4 ) (sum/4) (sum/4),我们可以用dfs遍历所有的情况。
这道题必须剪枝,不剪枝会超时,参考代码注释。
LeetCode题解:代码实现
LeetCode39. 组合总和
难度:mid
在一个数组中选任意个数凑成 t a r g e t target target 目标值,数组中的每个数可以选任意次。
这道题比较简单,直接看代码。
LeetCode题解:代码实现
LeetCode51. N 皇后
难度:hard
经典的N皇后问题,一个皇后的横、竖以及斜方向都不能有别的皇后。
这道题其实可以用全排列的思想做,我们枚举每一行的每个位置是否能放,如果能放则标记它的竖 c o l col col 、正对角线 d g dg dg 以及反对角线 u d g udg udg 为 t r u e true true。
另一种做法就是比较原始的搜索,上面的方法其实我们已经把问题抽象了,那么这个方法就是搜索每一个格子,是否能放皇后,当枚举到最后一个格子时,搜索也完成了。
这里更推荐第一种方法。
LeetCode题解:两种方法代码实现
BFS
LeetCode993. 二叉树的堂兄弟节点
难度:easy
DFS
我们先采用比较熟悉的dfs,从根节点开始遍历,当遍历到 x x x 时,我们记录一下它的深度以及父节点的值,遍历到 y y y 时同理,如果深度相同且父节点不同,则返回 t r u e true true 。
BFS
需要借助队列,先存入根节点,从根节点开始一层一层的搜索,搜索到这个节点就判断当前节点的值是否是我们的目标值,将每个节点的左右节点都 p u s h ( ) push() push() 进去, d e e p t h + 1 deepth + 1 deepth+1,判断完之后 p o p ( ) pop() pop() 掉。
我们可以做一个剪枝,当我们已经遍历到 x x x 和 y y y,我们可以直接 b r e a k break break,不需要遍历剩下的节点。
LeetCode题解:两种方法代码实现
LeetCode542. 01 矩阵
难度:mid
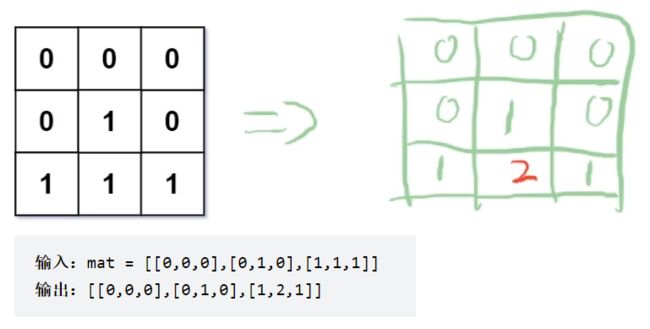
每一个 1 1 1 找到离它最近的一个 0 0 0 ,返回这个新的数组。
我们看示例2:
我们可以用bfs逆向搜索,找到对于某个 0 0 0 离这个 1 1 1 最近的距离,并标记在数组中。
每一个 1 1 1 都是被它最近的 0 0 0 扩散到的。
LeetCode题解:两种方法代码实现
LeetCode1091. 二进制矩阵中的最短路径
难度:mid
这道题就可以看做是BFS的经典例题了,直接看代码吧。
LeetCode题解:代码实现
LeetCode752. 打开转盘锁
难度:mid
给了我们一个转盘锁的数组 d e a d e n d s deadends deadends,记录着 “死亡数字”,从起始的 0000 0000 0000 状态转到我们的目标 t a r g e t target target 状态,期间不能与 d e a d e n d s deadends deadends 数组元素(死亡数字)相同;能解锁则返回最小步数,否则返回 − 1 -1 −1,此题仍然用bfs求解。
第一个样例就很清晰明了,注意中的字样转到了死亡数字 0102 0102 0102,故这种方式无法解锁:
我们可以把死亡数字理解成迷宫中的墙,标记一下。
LeetCode题解:代码实现
LeetCode剑指 Offer 13. 机器人的运动范围
难度:mid
也是很基础的bfs,只不过条件是下标的数位之和不能大于 k k k。
LeetCode题解:代码实现
总结
本章的重点就是
问题求解树,所有的搜索问题都可以转换为一棵树的形式。
对于深搜,每一个节点都代表着什么状态,它的状态都表现在递归的参数里;当然要注意剪枝,以及递归出口。
深搜(借助系统栈 递归),一搜到底,不要忘记恢复现场(回溯)
而对于广搜,它的状态表现在一个新的类,或者一个新的数组里;也要注意边界问题。
广搜(队列),层序遍历,寻找最优解(最小步数)
其实搜索本质上就是暴力枚举,但是我们可以加一些剪枝的优化,让我们搜索的方式尽可能快的找到答案。
最常用的搜索方式就是DFS(深度优先搜索)BFS(广度优先搜索)。
大部分的搜索方式都是这两种方式的基础上加入各种剪枝的判断优化。