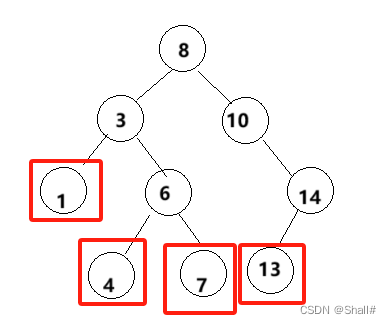
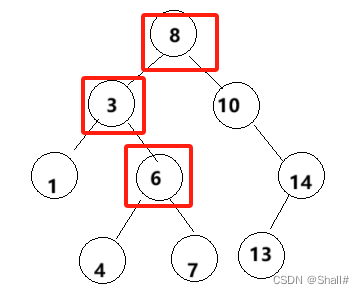
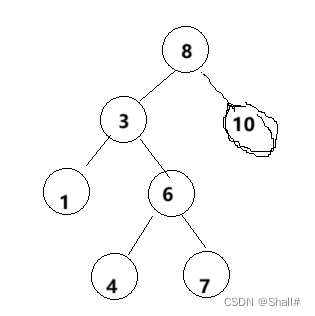
- 【Mars3d】支持的basemaps数组与layers数组的坐标系列举
mianmianwu
3d
问题场景:basemap是epsg4326的。,layer图层是epsg4450的。可以在一个页面中展示吗?回复:可以不同坐标系叠加,但layer图层是epsg4450的只支持arcgis动态服务,其他情况的不支持wmts只支持3个坐标系,EPSG4490\4326\3857说明:1.如果是其他坐标系的数据,需重新生产原数据为对应的支持的坐标系格式数据。2.支持的坐标系可以直接参数crs配置对应的
- YOLOv12_ultralytics-8.3.145_2025_5_27部分代码阅读笔记-split_dota.py
红色的山茶花
YOLO笔记深度学习
split_dota.pyultralytics\data\split_dota.py目录split_dota.py1.所需的库和模块2.defbbox_iof(polygon1:np.ndarray,bbox2:np.ndarray,eps:float=1e-6)->np.ndarray:3.defload_yolo_dota(data_root:str,split:str="train")->
- 基于 WebGL 与 GIS 的智慧垃圾分类三维可视化技术方案
图扑可视化
数字孪生三维可视化垃圾分类智慧环卫
图扑自主研发的HT可视化引擎,基于HTML5的WebGL与Canvas技术构建,形成了完整的2D/3D图形渲染体系。该引擎无需依赖第三方插件,通过纯JavaScript脚本调用API,即可实现跨平台的可视化交互体验,支持PC端、移动端及大屏终端的多屏协同。在三维渲染技术层面,引擎深度集成WebGL底层图形接口,构建了高效的轻量化处理体系。HT还支持3DTiles格式航拍倾斜摄影实景数据、城市建筑群
- python源码编译安装和常见问题解决
运维天坑笔记
python开发语言linux
python编译安装1、下载源码包wgethttps://www.python.org/ftp/python/3.9.10/Python-3.9.10.tgztar-zxfPython-3.9.10.tgzcdpython39/2、编译安装./configure--prefix=/usr/local/python39--enable-shared--enable-optimizationsmake
- 探索3D空间新维度:gltf-to-3d-tiles开源项目推荐
史琼鸽Power
探索3D空间新维度:gltf-to-3d-tiles开源项目推荐gltf-to-3d-tilesglTFto3dTilesConverter.ConvertglTFmodeltoGlb,b3dmor3dtilesformat.项目地址:https://gitcode.com/gh_mirrors/gl/gltf-to-3d-tiles在数字世界日益壮大的今天,高效地展示三维模型成为了技术领域的一大
- Linux-线程池
风君子吖
Linux系统编程linux运维服务器
文章目录前言一、线程池是什么?二、示例代码前言线程池主要是对之前内容的一个巩固,并且初步了解池化概念。一、线程池是什么?线程池就是提前开辟好一块空间,随时准备创造新线程来完成任务,可以理解为用空间来换时间,具体实现看以下示例代码。二、示例代码#include#include#include#include"lockGuard.hpp"#include"log.hpp"constintdefault
- Python语法笔记
XiTang1
python笔记开发语言
Python的基本语法1.计算机相关的名词知识1.1计算机的组成计算机之父:冯.诺依曼,根据冯.诺依曼结构体系,计算机是分为5部分的1.输入设备把信息传递到计算机中,比如键盘、鼠标2.输出设备信息从计算机中传递出来,比如音响、显示器、打印机等等3.存储区计算机被发明出来就是用于数据的存储和计算的计算机上有两个存储数据的设备:内存、硬盘硬盘:电脑上的磁盘分区,存储在硬盘中的数据都是持久化存储【只要不
- Python编程:实现文件比对
倔强老吕
C++与python交互编程python哈希算法
Python提供了多个用于文件比对的库,适用于不同的比较场景。以下是主要的文件比对库及其特点:1.标准库中的比对工具1.1filecmp模块功能:文件和目录比较特点:比较文件内容(浅层和深层比较)比较目录结构内置dircmp类用于目录比较典型用途:importfilecmp#文件比较filecmp.cmp('file1.txt','file2.txt',shallow=False)#目录比较com
- 用java,把12.25.pdf从最后一个点分割,得到pdf
连杰李
JAVA开发中遇到的问题javapdfpython
要在Java中从文件名12.25.pdf的最后一个点(.)分割文件名和扩展名,可以使用String类的lastIndexOf()和substring()方法。以下是一个示例代码:publicclassFileNameSplitter{publicstaticvoidmain(String[]args){StringfileName="12.25.pdf";//找到最后一个点的位置intlastDo
- 大模型呼叫中心场景分享之三十七:建筑行业的应用场景
大模型呼叫中心场景分享之三十七:建筑行业的应用场景作者:开源大模型呼叫中心系统FreeAICC一、项目前期咨询服务智能化1.24小时智能项目咨询台当潜在客户致电咨询商业综合体建设项目时:-需求精准识别:系统自动分析客户描述,识别"5万平米商业综合体""LEED认证""智慧建筑"等关键需求-方案即时生成:基于200+类似项目数据库,3分钟内生成初步方案框架-案例智能推荐:推送3个最匹配的已建成项目案
- 碳酸铈:稀土家族中的“小能手”
在稀土元素的大家族中,铈(Ce)以其广泛的用途和良好的化学稳定性,成为应用最为广泛的成员之一。而其化合物——碳酸铈,更是凭借其独特的物理化学性质,在多个工业领域中扮演着重要角色。一、基本性质与制备方法碳酸铈是一种白色粉末状固体,难溶于水,但可溶于酸。其制备通常采用铈盐与碳酸盐反应的方法,工艺流程简单、成本较低,是铈元素化合物生产中的重要中间体。二、工业应用概述作为铈元素的重要衍生物,碳酸铈在多个工
- Java领域Spring Cloud网关的配置与使用
Java大师兄学大数据AI应用开发
javaspringcloud开发语言ai
Java领域SpringCloud网关的配置与使用关键词:SpringCloudGateway、微服务网关、路由配置、过滤器、负载均衡、服务发现、API网关摘要:本文深入探讨SpringCloudGateway在Java微服务架构中的核心作用与实现原理。文章从网关的基本概念出发,详细解析其架构设计、路由配置、过滤器链等核心功能,并通过实际代码示例展示如何配置和使用SpringCloudGatewa
- Python, C ++,C #开发全球英才阐教版集结令APP
Geeker-2025
pythonc++c语言
以下是为使用**Python、C++和C#**开发**全球英才(阐教版)集结令APP**的深度技术方案,融合三语言优势构建跨平台、高智能的玄门英才聚合系统:---###一、系统架构设计```mermaidgraphTDA[多端客户端]-->B{C#阐道引擎}B-->C[C++玄法核心]C-->D[Python慧识层]D-->E[AI英才匹配]C-->F[天机推演]B-->G[三界通信]G-->H[
- Python, Rust 开发教育/医疗/文化资源去中心化分配APP
Geeker-2025
pythonrust
以下是为教育、医疗、文化资源设计的**去中心化分配APP**的完整技术方案,结合Python的灵活性和Rust的高性能与安全性,实现公平透明的资源分配:---###系统架构设计```mermaidgraphTDA[用户终端]-->B[区块链网络]A-->C[分配引擎]B-->D[智能合约]C-->E[资源数据库]D-->F[分配记录]subgraph技术栈C-.Rust.->G[核心分配算法]D-
- Python, Go 开发客户服务软件APP
Geeker-2025
pythongolang
以下是一个结合Python和Go开发的**客户服务软件APP**的完整技术方案,充分利用Python的AI能力和Go的高并发特性,构建高性能、智能化的客户服务系统:---###系统架构设计```mermaidgraphTDA[客户端]-->B[GoAPI网关]B-->C[工单管理]B-->D[实时聊天]B-->E[知识库]B-->F[AI引擎]C-->G[工单数据库]D-->H[消息队列]F-->
- 常见JAVA集合面试题(自用整理,持续更新)
一、简要介绍Java集合框架的整体架构1.Java集合框架主要分为两大接口体系:Collection和Map。2.Collection是单列集合的根接口,下面又有三个子接口,分别是List(有序、可重复)、Set(无序、不可重复)和Queue(队列)。3.Map是双列集合的根接口,用于存储键值对。4.以下是java集合的基础架构图5.Java集合框架的核心继承关系图(文本描述版)├─Collect
- c语言程序开发全局变量控制生存期
Bing2100
c语言算法开发语言
在C语言中,全局变量的生存期与程序一致,若管理不当易引发初始化顺序混乱、资源泄漏等问题。以下是针对C语言的全局变量优化方案,结合设计模式与语言特性规避生存期风险:一、模块化设计:用文件作用域替代全局作用域1.静态全局变量(文件内可见)适用场景:变量仅在单个源文件中使用,避免被其他文件意外修改。示例(module.c):c运行//module.cstaticintmoduleState=0;//仅在
- (C++)学生管理系统(测试版)(map数组的应用)(string应用)(引用)(C++教学)(C++项目)
双叶836
C++基础教学STLC++C++项目c++算法开发语言数据结构后端
源代码:#include//输入输出流库,提供cin/cout等基本I/O功能#include//映射容器库,提供map数据结构(键值对集合)#include//字符串库,提供string类及字符串操作#include//输入输出格式化库,提供setw等格式化控制usingnamespacestd;//使用标准命名空间,避免写std::前缀//定义学生结构体:包含多个相关数据的复合类型struct
- YOLOv12_ultralytics-8.3.145_2025_5_27部分代码阅读笔记-augment.py
augment.pyultralytics\data\augment.py目录augment.py1.所需的库和模块2.classBaseTransform:3.classCompose:4.classBaseMixTransform:5.classCutMix(BaseMixTransform):6.classCopyPaste(BaseMixTransform):7.defv8_transfo
- 基于nodejs+vue.js服装商店电子商务管理系统
如果你是一个小白,你不懂得像javaPHP、Python等编程语言,那么Node.js是一个非常好的选择。采用vscode软件开发,配套软件安装.包安装调试部署成功,有视频讲解前端:html+vue+elementui+jQuery、js、css数据库:mysql,Navicatvue框架于Node运行环境的Web框架,随着互联网技术的飞速发展,世界逐渐成了一个地球村,空间的距离也不再是那么重要。
- Docker 跨平台支持:从 Linux 到 macOS 的容器化开发实践
you的日常
容器技术Docker性能优化实践dockerlinuxmacos容器运维
Docker容器的理念是“一次构建,处处运行”,旨在解决应用程序在不同环境中部署的兼容性问题。然而,这一承诺的实现,在非原生Linux系统(如macOS和Windows)上,需要巧妙的底层机制来支撑。对于开发者而言,理解DockerDesktop在这些操作系统上的工作原理,特别是其虚拟机机制和文件共享策略,对于优化开发体验和解决潜在性能问题至关重要。本文将深入探讨Docker如何在macOS和Wi
- 《Effective Python》第十一章 性能——延迟加载模块,通过动态导入减少 Python 程序启动时间
不学无术の码农
EffectivePython精读笔记python开发语言
引言本文基于《EffectivePython:125SpecificWaystoWriteBetterPython,3rdEdition》第11章:性能中的Item98:Lazy-LoadModuleswithDynamicImportstoReduceStartupTime。本文旨在总结书中关于延迟加载模块的核心观点,并结合我自己的开发经验,深入探讨其在实际项目中的应用场景与优化价值。Pytho
- 90.xilinx复位低电平(一般使用低电平复位)
cmc1028
笔记笔记
XilinxFPGA中的寄存器(Flip-Flop)**确实支持异步复位**,但具体实现方式取决于你使用的设计方法(HDL代码风格或原语实例化)。以下是详细说明:---###1.**Xilinx寄存器的复位特性**-**同步复位和异步复位均支持**,但需要通过代码或原语明确指定。-异步复位的信号通常会直接连接到寄存器的`CLR`(Clear,低电平有效)或`PRE`(Preset,高电平有效)端口
- C++网络编程Socket网络编程基础入门
weixin_47868976
网络c++开发语言
Socket网络编程基础入门-从理论到实践1.Socket基本概念1.1什么是Socket?Socket(套接字)是网络编程的基础,它是应用层与传输层之间的抽象接口。简单来说,Socket就是网络通信的端点,就像电话的听筒一样,用于发送和接收数据。在你的FileHub项目中,Socket被封装在多个层次中://从net/Socket.h可以看到Socket的封装classSocket:noncop
- 「日拱一码」010 Python常用库——statistics
胖达不服输
「日拱一码」pythonpython常用库statistics
目录平均值相关mean():计算算术平均值,即所有数值相加后除以数值的个数fmean():与mean()类似,但使用浮点运算,速度更快,精度更高geometric_mean():计算几何平均值,即所有数值相乘后开n次方根(n为数值的个数)harmonic_mean():计算调和平均值,即数值个数除以每个数值的倒数之和median():计算中位数,即将一组数值按大小顺序排列后位于中间的数。如果数值个
- python日记Day17——Pandas之Excel处理
石石石大帅
Python笔记excelpython数据分析
python日记——Pandas之Excel处理创建文件importpandasaspddf=pd.DataFrame({'ID':[1,2,3],'Name':['Tom','BOb','Gigi']})df.to_excel("C:/Temp/Output.xlsx")print("done!")读取文件importpandasaspdpeople=pd.read_excel("C:/Temp
- 分布式锁的实现方式:使用 Redisson 实现分布式锁( Spring Boot )
weixin_43833540
分布式springboot后端
Redisson提供了分布式和可扩展的Java数据结构,包括分布式锁的实现。1.添加依赖在pom.xml中添加Redisson依赖:org.redissonredisson-spring-boot-starter3.16.42.配置Redisson客户端创建Redisson配置类:importorg.redisson.Redisson;importorg.redisson.api.Redisson
- 利用ADB实现PC与Android设备的通信与数据交互
虾仁芝麻卷
本文还有配套的精品资源,点击获取简介:本文详细介绍了如何使用AndroidDebugBridge(ADB)实现PC与Android终端的通信,特别是通过Java编程语言的应用。介绍了配置ADB、设备连接、端口映射、Java编程实现设备通信、异常处理以及关闭连接等关键步骤,并强调了该技术在多种开发场景下的应用和注意事项。1.ADB功能与重要性AndroidDebugBridge(ADB)是一种多功能
- FinalShell 4:Linux系统SSH连接与远程管理工具应用指南
虾仁芝麻卷
本文还有配套的精品资源,点击获取简介:FinalShell4是专为Linux系统打造的集成化远程管理工具,以其强大的SSH连接功能著称,支持多种操作系统平台。该软件集成了丰富的终端模拟、会话管理、文件传输和性能优化等特性,提高了IT运维的效率和安全性。其内置的脚本支持和实时监控功能进一步加强了服务器管理的自动化和便捷性,使其成为IT专业人员的得力助手。1.SSH连接与安全远程操作SSH(Secur
- android 多通道音频,支持多通道录音
虾仁芝麻卷
android多通道音频
原生Android只支持2channel的录音。可是偏偏会有多mic的需求,比如说语音识别。目前已知TDM协议可以将多mic数据从kernel送到hal,从内核空间搬运到用户空间中。可是原生AudioRecord接口是完全不支持多channel录音数据的采集的,怎么修改,才能让原生进行支持呢?我们就从AudioRecord的构造函数开始往下研究。无论行不行,都要研究出个所以然来!我们如果写个录音a
- Spring中@Value注解,需要注意的地方
无量
springbean@Valuexml
Spring 3以后,支持@Value注解的方式获取properties文件中的配置值,简化了读取配置文件的复杂操作
1、在applicationContext.xml文件(或引用文件中)中配置properties文件
<bean id="appProperty"
class="org.springframework.beans.fac
- mongoDB 分片
开窍的石头
mongodb
mongoDB的分片。要mongos查询数据时候 先查询configsvr看数据在那台shard上,configsvr上边放的是metar信息,指的是那条数据在那个片上。由此可以看出mongo在做分片的时候咱们至少要有一个configsvr,和两个以上的shard(片)信息。
第一步启动两台以上的mongo服务
&nb
- OVER(PARTITION BY)函数用法
0624chenhong
oracle
这篇写得很好,引自
http://www.cnblogs.com/lanzi/archive/2010/10/26/1861338.html
OVER(PARTITION BY)函数用法
2010年10月26日
OVER(PARTITION BY)函数介绍
开窗函数 &nb
- Android开发中,ADB server didn't ACK 解决方法
一炮送你回车库
Android开发
首先通知:凡是安装360、豌豆荚、腾讯管家的全部卸载,然后再尝试。
一直没搞明白这个问题咋出现的,但今天看到一个方法,搞定了!原来是豌豆荚占用了 5037 端口导致。
参见原文章:一个豌豆荚引发的血案——关于ADB server didn't ACK的问题
简单来讲,首先将Windows任务进程中的豌豆荚干掉,如果还是不行,再继续按下列步骤排查。
&nb
- canvas中的像素绘制问题
换个号韩国红果果
JavaScriptcanvas
pixl的绘制,1.如果绘制点正处于相邻像素交叉线,绘制x像素的线宽,则从交叉线分别向前向后绘制x/2个像素,如果x/2是整数,则刚好填满x个像素,如果是小数,则先把整数格填满,再去绘制剩下的小数部分,绘制时,是将小数部分的颜色用来除以一个像素的宽度,颜色会变淡。所以要用整数坐标来画的话(即绘制点正处于相邻像素交叉线时),线宽必须是2的整数倍。否则会出现不饱满的像素。
2.如果绘制点为一个像素的
- 编码乱码问题
灵静志远
javajvmjsp编码
1、JVM中单个字符占用的字节长度跟编码方式有关,而默认编码方式又跟平台是一一对应的或说平台决定了默认字符编码方式;2、对于单个字符:ISO-8859-1单字节编码,GBK双字节编码,UTF-8三字节编码;因此中文平台(中文平台默认字符集编码GBK)下一个中文字符占2个字节,而英文平台(英文平台默认字符集编码Cp1252(类似于ISO-8859-1))。
3、getBytes()、getByte
- java 求几个月后的日期
darkranger
calendargetinstance
Date plandate = planDate.toDate();
SimpleDateFormat df = new SimpleDateFormat("yyyy-MM-dd");
Calendar cal = Calendar.getInstance();
cal.setTime(plandate);
// 取得三个月后时间
cal.add(Calendar.M
- 数据库设计的三大范式(通俗易懂)
aijuans
数据库复习
关系数据库中的关系必须满足一定的要求。满足不同程度要求的为不同范式。数据库的设计范式是数据库设计所需要满足的规范。只有理解数据库的设计范式,才能设计出高效率、优雅的数据库,否则可能会设计出错误的数据库.
目前,主要有六种范式:第一范式、第二范式、第三范式、BC范式、第四范式和第五范式。满足最低要求的叫第一范式,简称1NF。在第一范式基础上进一步满足一些要求的为第二范式,简称2NF。其余依此类推。
- 想学工作流怎么入手
atongyeye
jbpm
工作流在工作中变得越来越重要,很多朋友想学工作流却不知如何入手。 很多朋友习惯性的这看一点,那了解一点,既不系统,也容易半途而废。好比学武功,最好的办法是有一本武功秘籍。研究明白,则犹如打通任督二脉。
系统学习工作流,很重要的一本书《JBPM工作流开发指南》。
本人苦苦学习两个月,基本上可以解决大部分流程问题。整理一下学习思路,有兴趣的朋友可以参考下。
1 首先要
- Context和SQLiteOpenHelper创建数据库
百合不是茶
androidContext创建数据库
一直以为安卓数据库的创建就是使用SQLiteOpenHelper创建,但是最近在android的一本书上看到了Context也可以创建数据库,下面我们一起分析这两种方式创建数据库的方式和区别,重点在SQLiteOpenHelper
一:SQLiteOpenHelper创建数据库:
1,SQLi
- 浅谈group by和distinct
bijian1013
oracle数据库group bydistinct
group by和distinct只了去重意义一样,但是group by应用范围更广泛些,如分组汇总或者从聚合函数里筛选数据等。
譬如:统计每id数并且只显示数大于3
select id ,count(id) from ta
- vi opertion
征客丶
macoprationvi
进入 command mode (命令行模式)
按 esc 键
再按 shift + 冒号
注:以下命令中 带 $ 【在命令行模式下进行】,不带 $ 【在非命令行模式下进行】
一、文件操作
1.1、强制退出不保存
$ q!
1.2、保存
$ w
1.3、保存并退出
$ wq
1.4、刷新或重新加载已打开的文件
$ e
二、光标移动
2.1、跳到指定行
数字
- 【Spark十四】深入Spark RDD第三部分RDD基本API
bit1129
spark
对于K/V类型的RDD,如下操作是什么含义?
val rdd = sc.parallelize(List(("A",3),("C",6),("A",1),("B",5))
rdd.reduceByKey(_+_).collect
reduceByKey在这里的操作,是把
- java类加载机制
BlueSkator
java虚拟机
java类加载机制
1.java类加载器的树状结构
引导类加载器
^
|
扩展类加载器
^
|
系统类加载器
java使用代理模式来完成类加载,java的类加载器也有类似于继承的关系,引导类是最顶层的加载器,它是所有类的根加载器,它负责加载java核心库。当一个类加载器接到装载类到虚拟机的请求时,通常会代理给父类加载器,若已经是根加载器了,就自己完成加载。
虚拟机区分一个Cla
- 动态添加文本框
BreakingBad
文本框
<script> var num=1; function AddInput() { var str=""; str+="<input
- 读《研磨设计模式》-代码笔记-单例模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
public class Singleton {
}
/*
* 懒汉模式。注意,getInstance如果在多线程环境中调用,需要加上synchronized,否则存在线程不安全问题
*/
class LazySingleton
- iOS应用打包发布常见问题
chenhbc
iosiOS发布iOS上传iOS打包
这个月公司安排我一个人做iOS客户端开发,由于急着用,我先发布一个版本,由于第一次发布iOS应用,期间出了不少问题,记录于此。
1、使用Application Loader 发布时报错:Communication error.please use diagnostic mode to check connectivity.you need to have outbound acc
- 工作流复杂拓扑结构处理新思路
comsci
设计模式工作算法企业应用OO
我们走的设计路线和国外的产品不太一样,不一样在哪里呢? 国外的流程的设计思路是通过事先定义一整套规则(类似XPDL)来约束和控制流程图的复杂度(我对国外的产品了解不够多,仅仅是在有限的了解程度上面提出这样的看法),从而避免在流程引擎中处理这些复杂的图的问题,而我们却没有通过事先定义这样的复杂的规则来约束和降低用户自定义流程图的灵活性,这样一来,在引擎和流程流转控制这一个层面就会遇到很
- oracle 11g新特性Flashback data archive
daizj
oracle
1. 什么是flashback data archive
Flashback data archive是oracle 11g中引入的一个新特性。Flashback archive是一个新的数据库对象,用于存储一个或多表的历史数据。Flashback archive是一个逻辑对象,概念上类似于表空间。实际上flashback archive可以看作是存储一个或多个表的所有事务变化的逻辑空间。
- 多叉树:2-3-4树
dieslrae
树
平衡树多叉树,每个节点最多有4个子节点和3个数据项,2,3,4的含义是指一个节点可能含有的子节点的个数,效率比红黑树稍差.一般不允许出现重复关键字值.2-3-4树有以下特征:
1、有一个数据项的节点总是有2个子节点(称为2-节点)
2、有两个数据项的节点总是有3个子节点(称为3-节
- C语言学习七动态分配 malloc的使用
dcj3sjt126com
clanguagemalloc
/*
2013年3月15日15:16:24
malloc 就memory(内存) allocate(分配)的缩写
本程序没有实际含义,只是理解使用
*/
# include <stdio.h>
# include <malloc.h>
int main(void)
{
int i = 5; //分配了4个字节 静态分配
int * p
- Objective-C编码规范[译]
dcj3sjt126com
代码规范
原文链接 : The official raywenderlich.com Objective-C style guide
原文作者 : raywenderlich.com Team
译文出自 : raywenderlich.com Objective-C编码规范
译者 : Sam Lau
- 0.性能优化-目录
frank1234
性能优化
从今天开始笔者陆续发表一些性能测试相关的文章,主要是对自己前段时间学习的总结,由于水平有限,性能测试领域很深,本人理解的也比较浅,欢迎各位大咖批评指正。
主要内容包括:
一、性能测试指标
吞吐量、TPS、响应时间、负载、可扩展性、PV、思考时间
http://frank1234.iteye.com/blog/2180305
二、性能测试策略
生产环境相同 基准测试 预热等
htt
- Java父类取得子类传递的泛型参数Class类型
happyqing
java泛型父类子类Class
import java.lang.reflect.ParameterizedType;
import java.lang.reflect.Type;
import org.junit.Test;
abstract class BaseDao<T> {
public void getType() {
//Class<E> clazz =
- 跟我学SpringMVC目录汇总贴、PDF下载、源码下载
jinnianshilongnian
springMVC
----广告--------------------------------------------------------------
网站核心商详页开发
掌握Java技术,掌握并发/异步工具使用,熟悉spring、ibatis框架;
掌握数据库技术,表设计和索引优化,分库分表/读写分离;
了解缓存技术,熟练使用如Redis/Memcached等主流技术;
了解Ngin
- the HTTP rewrite module requires the PCRE library
流浪鱼
rewrite
./configure: error: the HTTP rewrite module requires the PCRE library.
模块依赖性Nginx需要依赖下面3个包
1. gzip 模块需要 zlib 库 ( 下载: http://www.zlib.net/ )
2. rewrite 模块需要 pcre 库 ( 下载: http://www.pcre.org/ )
3. s
- 第12章 Ajax(中)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- Optimize query with Query Stripping in Web Intelligence
blueoxygen
BO
http://wiki.sdn.sap.com/wiki/display/BOBJ/Optimize+query+with+Query+Stripping+in+Web+Intelligence
and a very straightfoward video
http://www.sdn.sap.com/irj/scn/events?rid=/library/uuid/40ec3a0c-936
- Java开发者写SQL时常犯的10个错误
tomcat_oracle
javasql
1、不用PreparedStatements 有意思的是,在JDBC出现了许多年后的今天,这个错误依然出现在博客、论坛和邮件列表中,即便要记住和理解它是一件很简单的事。开发者不使用PreparedStatements的原因可能有如下几个: 他们对PreparedStatements不了解 他们认为使用PreparedStatements太慢了 他们认为写Prepar
- 世纪互联与结盟有感
阿尔萨斯
10月10日,世纪互联与(Foxcon)签约成立合资公司,有感。
全球电子制造业巨头(全球500强企业)与世纪互联共同看好IDC、云计算等业务在中国的增长空间,双方迅速果断出手,在资本层面上达成合作,此举体现了全球电子制造业巨头对世纪互联IDC业务的欣赏与信任,另一方面反映出世纪互联目前良好的运营状况与广阔的发展前景。
众所周知,精于电子产品制造(世界第一),对于世纪互联而言,能够与结盟