C语言实现四进制(四叉树)、十进制的Morton码
一、前言:
由《地理信息信息系统与原理》《地理信息系统基础》介绍,感觉有点意思,故想用C语言实现一下,顺便梳理相关内容。
前提知识:
叶节点:即没有子节点的节点。
线性四叉数只存储最后叶节点信息,包括叶节点的位置、深度和网格值。
地址码(Morton码):线性四叉树叶节点遵照一定的规则,隐含了叶节点位置信息的编号。
拓展:
3维空间xyz 的 32 位的莫顿码 编码方式zyxzyx, 每个维度用10bit 表示(0~1023)。
树的结点:包含一个数据元素及若干指向子树的分支;
孩子结点:结点的子树的根称为该结点的孩子;
双亲结点:B 结点是A 结点的孩子,则A结点是B 结点的双亲;
兄弟结点:同一双亲的孩子结点; 堂兄结点:同一层上结点;
祖先结点: 从根到该结点的所经分支上的所有结点子孙结点:以某结点为根的子树中任一结点都称为该结点的子孙
结点层:根结点的层定义为1;根的孩子为第二层结点,依此类推;
树的深度:树中最大的结点层
结点的度:结点子树的个数
树的度: 树中最大的结点度。
叶子节点:也叫终端结点,是度为 0 的结点;
分枝结点:度不为0的结点;
有序树:子树有序的树,如:家族树;
无序树:不考虑子树的顺序;
二、基本原理:
两种方法:
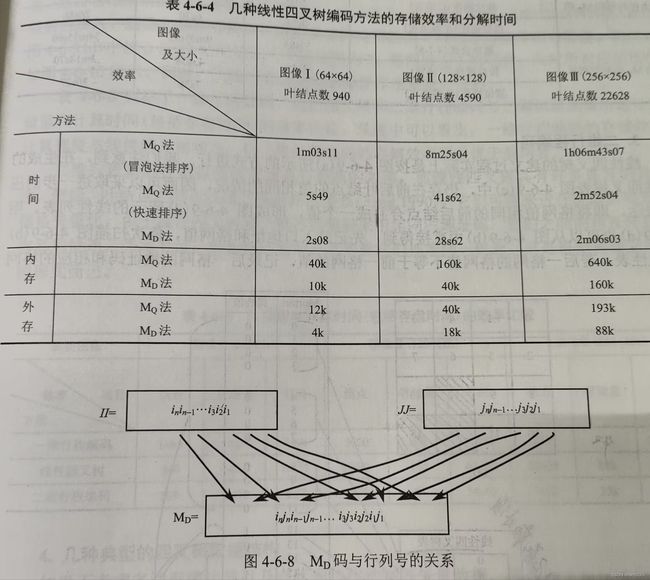
基于四进制Morton码的生成和四叉数的建立过程有两种不同方案
1.自上而下分裂的方式在建立四叉数的过程中逐步产生Morton码;
2.先计算每个格网的Morton码,然后按一定扫描方式自下而上合并建立四叉数。
自下而上与自上而下生成的四叉数一致,但前者的效率更高
对于第一种方法的Morton码:
第一步:分割子象限,标号0,1,2,3分别表示左上,右上,左下,右下四个子象限。
第二步:进行检测,如有需要继续细分。
分割过程中,标号的位数不断增加,这种标号即Morton码。
且Morton码的每一位数字都是不大于3的四进制数,每经过一次分割,增加一位数字,分割次数越多,所得子区域越小,相应的Morton码值越大。
最后结点的Morton码值是所有各位上相应象限值相加,MQ=q1q2q3..qn=q1*10^(k-1)+q2*10^(k-2)...+qk
对于第二种方法的Morton码:
1.将十进制的行列号转化为二进制数表示
2.依据MQ=2*Ib(二进制行号)+Jb(二进制列号)
三、代码实现:
小试牛刀:
理解一下四进制的Morton码:
#include
#include
//计算MQ值
int calculateMq(int Ib,int Jb)
{
return (2 * Ib + Jb);
}
//计算十进制数
int tenTransToTwo(int II)
{
int sum = 0;//用于存放转化后的二进制
int n = 0;//用于转化输出形式的指数
while (II > 1)//判断除二取余是否完成
{//逆序存储
sum += ((II % 2)*pow(10,n));
II = (II- II % 2)/2;
n++;
}
sum += (II * pow(10, n));
return sum;
}
int main()
{
//提示用户输入
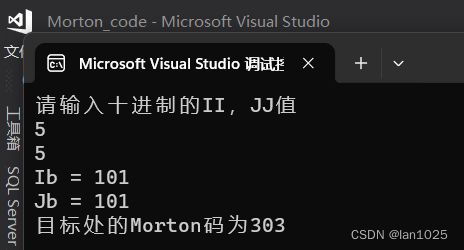
printf("请输入十进制的II,JJ值\n");
//初始化与读取十进制数
int II=0;
int JJ=0;
scanf_s("%d", &II);
scanf_s("%d", &JJ);
//实现行和列的二进制转换
printf("%d\n", tenTransToTwo(II));
printf("%d\n", tenTransToTwo(JJ));
//输出四进制的Morton值(MQ值)
printf("%d\n", calculateMq(tenTransToTwo(II), tenTransToTwo(JJ)));
return 0;
} 输出结果:
四进制的缺点:
1.码内外内存开销大,多数语言不支持四进制变量。
2.运算效率不高
因此Mark等人(1989)建议采用十进制的Morton码作为线性四叉数的地址码
再次体验:
十进制的Morton码:
法一:
基于数学公式的计算法
#include
#include
//计算MQ值
int calculateMq(int Ib, int Jb)
{
return (2 * Ib + Jb);
}
//计算十进制数
int tenTransToTwo(int II)
{
int sum = 0;//用于存放转化后的二进制
int n = 0;//用于转化输出形式的指数
while (II > 1)//判断除二取余是否完成
{//逆序存储
sum += ((II % 2)*pow(10, n));
II = (II - II % 2) / 2;
n++;
}
sum += (II * pow(10, n));
return sum;
}
//计算二进制数
int twoTransToFour(int transtedTwo)
{
int sum = 0;//用于存储四进制数
int n = 0;//用于转化输出形式的指数
int digit = 0;//用于暂存每一位数;
//遵循逆序输出的原则,正序存入
while(transtedTwo>0)
{
digit = transtedTwo % 2;
transtedTwo /= 2;
sum += (digit*pow(4, n));
n++;
}
//返回数组即返回四进制数
return sum;
}
int main()
{
//提示用户输入
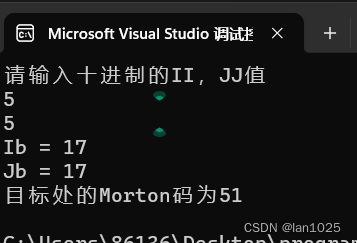
printf("请输入十进制的II,JJ值\n");
//初始化与读取十进制数
int II = 0;
int JJ = 0;
scanf_s("%d", &II);
scanf_s("%d", &JJ);
实现行和列的二进制转换
//printf("Ib = %d\n", tenTransToTwo(II));
//printf("Jb = %d\n", tenTransToTwo(JJ));
输出四进制的Morton值(MQ值)
//printf("目标处的Morton码为%d\n", calculateMq(tenTransToTwo(II), tenTransToTwo(JJ)));
//实现行和列的四进制转换
printf("Ib = %d\n", twoTransToFour(II));
printf("Jb = %d\n", twoTransToFour(JJ));
//输出十进制的Morton值(MQ值)
printf("目标处的Morton码为%d\n", calculateMq(twoTransToFour(II), twoTransToFour(JJ)));
return 0;
} 法二:
基于按位操作的运算法,为了简化对按位操作符的使用作者打算使用数组模拟。
#include
#include
//计算十进制数
int tenTransToTwo(int II)
{
int sum = 0;//用于存放转化后的二进制
int n = 0;//用于转化输出形式的指数
while (II > 1)//判断除二取余是否完成
{//逆序存储
sum += ((II % 2)*pow(10,n));
II = (II- II % 2)/2;
n++;
}
sum += (II * pow(10, n));
return sum;
}
//计算二进制数
int MyBitOperator(int transtedTwo1 , int transtedTwo2)
{
int sum = 0;//用于存储四进制数
int i=0;//移动数组下标
//遵循逆序输出的原则,正序存入
int arr[8] = { 0 };//用于存放II和JJ的位,偶数(和0)为II位,奇数为JJ位
while (transtedTwo1 > 0)
{
arr[0+i] = transtedTwo1% 2;//0,2,4,6
transtedTwo1 /= 10;
i += 2;
}
i = 0;
while (transtedTwo2 > 0)
{
arr[1+i] = transtedTwo2 % 2;//1,3,5,7
transtedTwo2 /= 10;
i += 2;
}
//计算Md
int n = 0;//用于转化输出形式的指数
for (int i = (sizeof(arr) / sizeof(arr[0]))-3; i >=0; i--)//前面数组冗余
{
if (arr[i] > 0) {
sum += (arr[i] * pow(2, n));
printf("%d\n", sum);
}
n++;
}
//返回数组即返回四进制数
return sum;
}
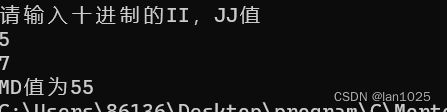
int main() {
//提示用户输入
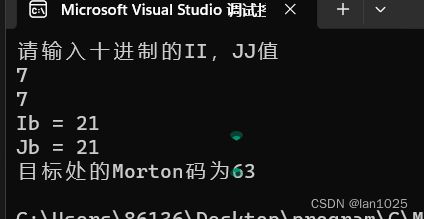
printf("请输入十进制的II,JJ值\n");
//初始化与读取十进制数
int II = 0;
int JJ = 0;
scanf_s("%d", &II);
scanf_s("%d", &JJ);
printf("MD值为%d", MyBitOperator(tenTransToTwo(II), tenTransToTwo(JJ)));
return 0;
}
输出结果:
法一:
法二: