LSTM 08:超详细LSTM调参指南
本文代码运行环境:
- cudatoolkit = 10.1.243
- cudnn = 7.6.5
- tensorflow-gpu = 2.1.0
- keras-gpu = 2.3.1
相关文章
LSTM 01:理解LSTM网络及训练方法
LSTM 02:如何为LSTM准备数据
LSTM 03:如何使用Keras编写LSTM
LSTM 04:4种序列预测模型及Keras实现
LSTM 05:Keras实现多层LSTM进行序列预测
LSTM 06:Keras实现CNN-LSTM模型
LSTM 07:Keras实现Encoder-Decoder LSTM
LSTM 08:超详细LSTM调参指南
文章目录
- 相关文章
- 8. 如何诊断和调整LSTM
-
- 8.1 可靠地评估LSTM模型
-
- 8.1.1 初学者易犯的错误
- 8.1.2 评估模型性能
- 8.1.3 评估随机模型的技巧
- 8.1.4 神经网络有多不稳定?
- 8.1.5 评估重复多少次?
- 8.2 诊断欠拟合和过拟合
-
- 8.2.1 Keras中的实现
- 8.2.2 Diagnostic Plots
- 8.2.3 欠拟合
- 8.2.4 较好拟合
- 8.2.5 过拟合
- 8.2.6 多次运行
- 8.3 调试问题方法
-
- 8.3.1 数值缩放
- 8.3.2 编码
- 8.3.3 平稳性
- 8.3.4 输入序列长度
- 8.3.5 序列模型类型
- 8.4 调试模型架构
-
- 8.4.1 架构(Architecture)
- 8.4.2 记忆单元(Memory Cells)
- 8.4.3 隐藏层 (Hidden Layers)
- 8.4.4 权重初始化 (Weight Initialization)
- 8.4.5 激活函数(Activation Functions)
- 8.5 调试学习行为
-
- 8.5.1 优化算法(Optimization Algorithm)
- 8.5.2 学习率(Learning Rate)
- 8.5.3 批次大小(Batch Size)
- 8.5.4 正则化(Regularization)
- 8.5.5 适时停止训练
- 8.6 拓展阅读
8. 如何诊断和调整LSTM
本文讨论了如何调整LSTM超参数。主要内容包括以下三部分:
- 如何对LSTM模型进行可靠的评估。
- 如何使用学习曲线诊断LSTM模型。
- 如何调整LSTM模型的问题框架,结构和学习行为。
8.1 可靠地评估LSTM模型
本小节,讨论了在不可见数据上对LSTM模型的进行可靠估计的过程。
8.1.1 初学者易犯的错误
一般流程是:训练模型适使其拟合 fit() 训练数据,在测试集上评估 evaluate() 模型,然后打印模型性能。也有使用 k-fold交叉验证(k-fold cross-validation)来评估模型,然后打印模型的技能。这都是初学者常犯的错误。
以上两种方法看起来是对的,但细想其实不然。有很关键的一点不得不注意:深度学习模型是随机的。诸如LSTM之类的人工神经网络在拟合数据集时有随机性,例如随机初始化权重和随机梯度下降期间每个epoch的数据都会随机打乱(shuffle)。这意味着每次将相同的模型拟合到相同的数据时,它可能会给出不同的预测,进而具有不同的总体表现。
8.1.2 评估模型性能
如果数据有限,需要通过评估找出性能最好的模型(调整超参数,使模型性能最好)。
将数据分成两部分,第一部分用来拟合模型或特定的模型配置,并使用拟合好的模型对第二部分进行预测,然后评估这些预测的性能。这被称为train-test split,模型的性能可以通过在新数据上的预测表现判断(泛化性能)。下面是拆分训练集测试集评估模型的伪代码:
train, test = random_split(data)
model = fit(train.X, train.y)
predictions = model.predict(test.X)
skill = compare(test.y, predictions)
如果数据集比较大或模型训练非常慢,那么训练集测试集分割是一个很好的方法,但是由于数据的随机性(导致模型引入方差),模型的性能得分会很高。这意味着同一模型对不同数据的拟合将给出不同的模型性能得分。如果计算资源充足,可以使用k-fold交叉验证。但在深度学习中使用大型数据集以及模型训练速度较慢,这通常是不太可行的。
8.1.3 评估随机模型的技巧
随机模型,如深层神经网络,增加了随机性操作(如随机初始化权重和随机梯度下降)。这种额外的随机性使模型在学习时具有更大的灵活性,但会使模型不太稳定(例如,在相同的数据上训练相同的模型会产生不同的结果)。这与在不同数据上训练同一模型时给出不同结果的模型方差不同。
为了得到一个可靠(鲁棒)的模型性能估计,必须考虑并且控制这个额外的方差来源。**一种可靠的方法是多次重复评估随机模型的实验。**可以参考如下伪代码:
scores = list()
for i in repeats:
train, test = random_split(data)
model = fit(train.X, train.y)
predictions = model.predict(test.X)
skill = compare(test.y, predictions)
scores.append(skill)
final_skill = mean(scores)
8.1.4 神经网络有多不稳定?
这取决于模型要解决的问题、网络及其配置。可以使用多次(几十,几百或上千次)对同一数据计算同一模型,并且只改变随机数生成器,然后评估技能得分的平均值和标准差。标准差(分数与平均分的平均距离)能反映出模型有多不稳定。
8.1.5 评估重复多少次?
几十,几百或上千次不等,取决于时间和计算机资源的限制,随着次数增多,误差也在下降(比如标准差)。更严谨的做法是首先研究重复次数对估计模型性能的影响,以及标准差的计算(平均估计性能与实际总体平均值的差异有多大)。
8.2 诊断欠拟合和过拟合
本小节,讨论了如何通过绘制学习曲线图来诊断过拟合和欠拟合。
8.2.1 Keras中的实现
训练开始后,可以通过查看模型的性能来了解模型的许多行为。LSTM模型通过调用fit()函数进行训练。此函数返回一个名为.history的变量,该变量包含了在编译模型期间的损失,准确率。这些信息会在每个epoch训练结束之后打印。
如果fit方法中设置了validation_data=(testX, testy)参数,那么.history 返回一个有四个键值对的字典,包括训练集上的准确率'accuracy',损失'loss';验证集上的准确率'accuracy',损失'val_loss',相应的值是各项指标单值的列表。比如,训练5个epoch的返回值:
...
history = model.fit(trainX, trainy,
epochs=epochs,
batch_size=batch_size,
verbose=verbose,
validation_data=(testX, testy),
callbacks=[summary])
print("history.history:{}".format(history.history))
#输出:
history.history:{'loss': [0.6198216109203176, 0.22001621517898987, 0.14948655201184996, 0.12273854326955383, 0.12327274605550756],
'accuracy': [0.74428725, 0.91920567, 0.9428727, 0.953346, 0.95048964],
'val_loss': [0.5575803409279667, 0.4091062663836594, 0.39247380317769337, 0.3639399050404692, 0.3881000212997623],
'val_accuracy': [0.8187988, 0.8649474, 0.89650494, 0.8975229, 0.8982016]}
注意:在TensorFlow 1.x版本为后端的Keras中,model.fit() 返回的字典中的键为’acc’,‘loss’,‘val_acc’,‘val_loss’。在绘制图像的时候注意!
针对训练集验证集的划分,Keras还允许指定一个单独的验证数据集,同时拟合模型,该模型也可以使用相同的损失和度量进行评估。这可以通过在fit()中设置validation_split参数来完成,该参数使用部分训练数据作为验证数据集(用介于0.0和1.0之间数表示验证集比例)。
...
history = model.fit(X, Y, epochs=100, validation_split=0.33)
如果数据集已经将训练集和验证集划分,则可以通过设置validation data参数传递X和y数据集的元组来完成。例如在HAR分类任务中,valX表示数据,valY表示分类标签(0,类别数-1)。
history = model.fit(X, Y, epochs=100, validation_data=(valX, valY))
8.2.2 Diagnostic Plots
LSTM模型的训练日志可用于诊断模型的行为。可以使用Matplotlib库打印模型的性能。例如,可以按如下方式绘制训练损失与测试损失:
import matplotlib.pyplot as plt
...
history = model.fit(X, Y, epochs=100, validation_data=(valX, valY))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model train vs validation loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','validation'], loc='upper right')
plt.show()
创建和查看这些图可以帮助了解可能要尝试的新配置,以便从模型中获得更好的性能。
8.2.3 欠拟合
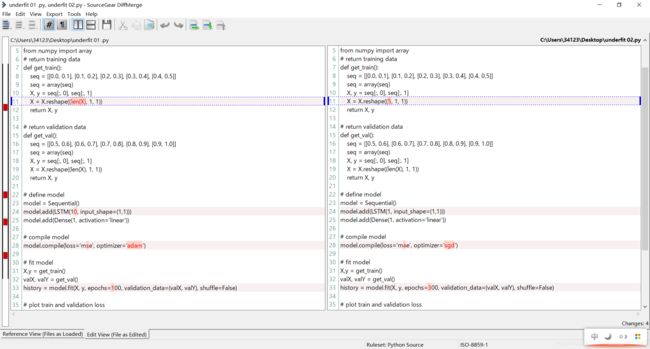
欠拟合模型在训练数据集上表现良好,而在测试数据集上表现较差(泛化能力不好)。这可以从训练损失低于验证损失的图中诊断出来,并且验证损失有一个趋势,表明有可能进一步改进。下面提供了一个未完全拟合的LSTM模型的示例。
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
import matplotlib.pyplot as plt
from numpy import array
# return training data
def get_train():
seq = [[0.0, 0.1], [0.1, 0.2], [0.2, 0.3], [0.3, 0.4], [0.4, 0.5]]
seq = array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((len(X), 1, 1))
return X, y
# return validation data
def get_val():
seq = [[0.5, 0.6], [0.6, 0.7], [0.7, 0.8], [0.8, 0.9], [0.9, 1.0]]
seq = array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((len(X), 1, 1))
return X, y
# define model
model = Sequential()
model.add(LSTM(10, input_shape=(1,1)))
model.add(Dense(1, activation='linear'))
# compile model
model.compile(loss='mse', optimizer='adam')
# fit model
X,y = get_train()
valX, valY = get_val()
history = model.fit(X, y, epochs=100, validation_data=(valX, valY), shuffle=False)
# plot train and validation loss
plt.figure(figsize=(8,8),dpi=200)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model train vs validation loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','validation'], loc='upper right')
plt.show()
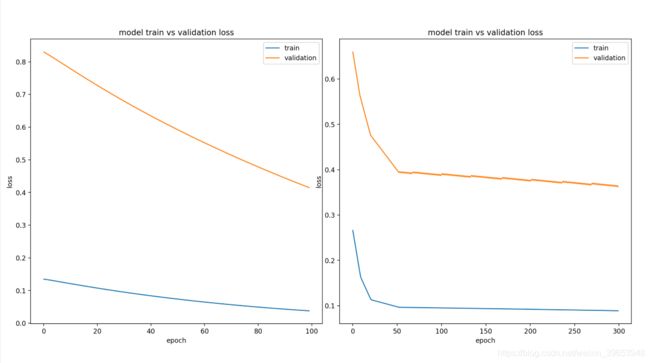
运行此示输出欠拟合模型特征的训练和验证损失。在这种情况下,可以增加训练epoch来提高性能。

或者,如果在训练集上的性能优于验证集并且训练和验证损失已趋于平稳,则模型可能不适合。下面是memory cell不足的不合适模型的示例。
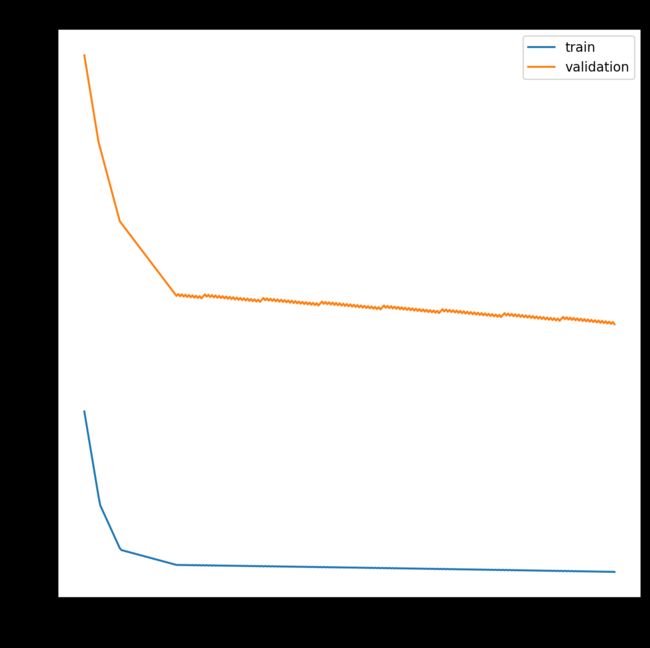
运行此示例显示了显示未配置的欠适合模型的特征。在这种情况下,可以通过增加模型的容量(例如隐藏层中的内存单元数或隐藏层数)来提高性能。
8.2.4 较好拟合
运行该示例显示训练和验证损失。理想情况下,希望看到这样的模型性能,尽管在处理拥有大量数据的挑战性问题时,这可能是不可能的。
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
import matplotlib.pyplot as plt
from numpy import array
# return training data
def get_train():
seq = [[0.0, 0.1], [0.1, 0.2], [0.2, 0.3], [0.3, 0.4], [0.4, 0.5]]
seq = array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((5, 1, 1))
return X, y
# return validation data
def get_val():
seq = [[0.5, 0.6], [0.6, 0.7], [0.7, 0.8], [0.8, 0.9], [0.9, 1.0]]
seq = array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((len(X), 1, 1))
return X, y
# define model
model = Sequential()
model.add(LSTM(10, input_shape=(1,1)))
model.add(Dense(1, activation='linear'))
# compile model
model.compile(loss='mse', optimizer='adam')
# fit model
X,y = get_train()
valX, valY = get_val()
history = model.fit(X, y, epochs=800, validation_data=(valX, valY), shuffle=False)
# plot train and validation loss
plt.figure(figsize=(8,8),dpi=200)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model train vs validation loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','validation'], loc='upper right')
plt.show()
8.2.5 过拟合
过拟合模型是指训练集的性能良好并持续改善,而验证集的性能提高到一定程度后开始下降的模型。这可从曲线图中诊断出来,在该曲线图中,训练损失向下倾斜,验证损失向下倾斜,到达一个拐点,然后又开始向上倾斜。下面的示例演示了一个过拟合的LSTM模型。
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
import matplotlib.pyplot as plt
from numpy import array
# return training data
def get_train():
seq = [[0.0, 0.1], [0.1, 0.2], [0.2, 0.3], [0.3, 0.4], [0.4, 0.5]]
seq = array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((5, 1, 1))
return X, y
# return validation data
def get_val():
seq = [[0.5, 0.6], [0.6, 0.7], [0.7, 0.8], [0.8, 0.9], [0.9, 1.0]]
seq = array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((len(X), 1, 1))
return X, y
# define model
model = Sequential()
model.add(LSTM(10, input_shape=(1,1)))
model.add(Dense(1, activation='linear'))
# compile model
model.compile(loss='mse', optimizer='adam')
# fit model
X,y = get_train()
valX, valY = get_val()
history = model.fit(X, y, epochs=1200, validation_data=(valX, valY), shuffle=False)
# plot train and validation loss
plt.figure(figsize=(8,8),dpi=200)
plt.plot(history.history['loss'][500:])
plt.plot(history.history['val_loss'][500:])
plt.title('model train vs validation loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train','validation'], loc='upper right')
plt.show()
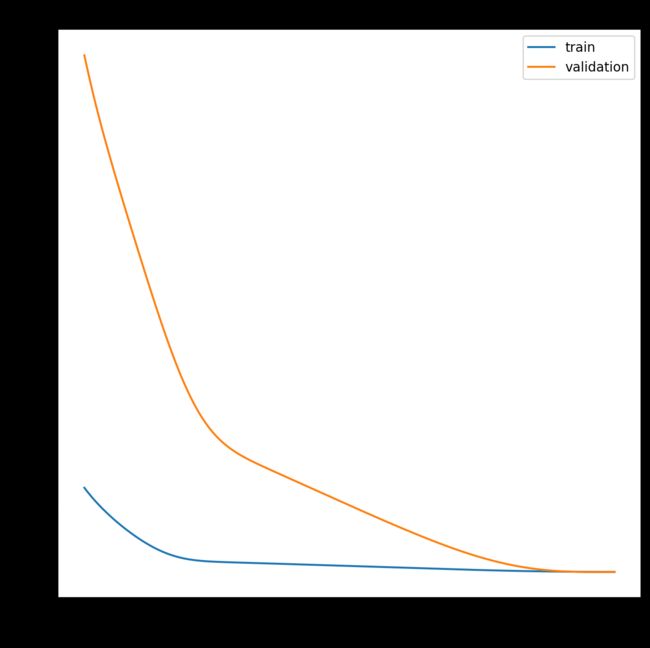
运行此示例将显示过拟合模型的验证丢失中的特征拐点。这可能是训练轮数(epoch)过多导致的。在这种情况下,模型训练可以在拐点处停止。或者,增加训练实例的数量。

正好拟合与过拟合对比
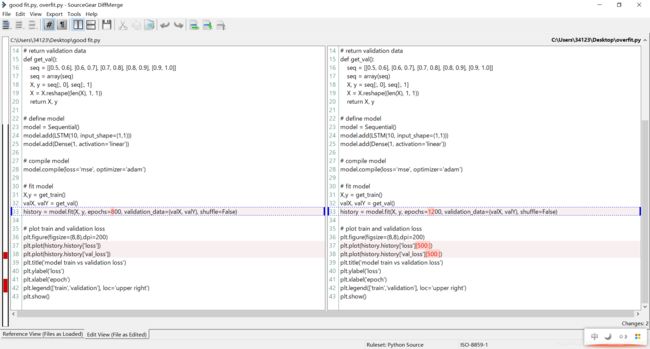

8.2.6 多次运行
LSTM是随机的,这意味着每次运行都会得到不同的诊断图。可以多次重复诊断运行(例如5、10或30)。然后,可以绘制每次运行的训练和验证跟踪,以便对模型随时间变化的行为提供更可靠的概念。在绘制每次运行的列车轨迹和验证损失之前,下面的示例多次运行同一个实验。
图中,在5次训练过程中,欠拟合趋势仍然存在,这可能是需要增加训练轮数的一个更有力的理由。

8.3 调试问题方法
本节概述了在调整序列预测问题时要考虑的最大因素。
8.3.1 数值缩放
评估不同数据值缩放方案对模型性能的影响。记住更新第一个隐藏层和/或输出层上的激活函数,以处理作为输入提供或作为输出预测的值的范围。一些方案包括:
- Normalize values.(归一化)
- Standardize values.(标准化)
8.3.2 编码
评估不同值编码对模型性能的影响。标签序列,如字符或单词,通常是整数编码和one-hot编码。这是目前处理序列预测问题的常用的方法。编码方案包括:
- Real-value encoding.
- Integer encoding.
- One hot encoding.
8.3.3 平稳性
当处理实值序列(如时间序列)时,要考虑使序列保持平稳。
- 移除趋势(Remove Trends):如果序列包含均值的方差(例如趋势),则可以使用差异。
- 移除季节性(Remove Seasonality):如果序列包含周期性周期(例如季节性),则可以使用季节性调整。-
- 移除方差(Remove Variance):如果序列包含递增或递减方差,则可以使用对数或Box-Cox变换。
8.3.4 输入序列长度
输入序列长度的选择由要解决的问题决定,评估使用不同输入序列长度对模型性能的影响。当更新权值时,输入序列的长度也会影响通过时间的反向传播来估计误差梯度。它可以影响模型学习的速度和学习的内容。
8.3.5 序列模型类型
对于给定的序列预测问题,有4种主要的序列模型类型:
- One-to-one
- One-to-many
- Many-to-one
- Many-to-many
Keras 都支持以上序列模型。使用每个序列模型类型为问题设置框架,并评估模型性能,以帮助为需要解决的问题选择框架。
8.4 调试模型架构
本节概述了在调整LSTM模型的结构时影响比较大的方面。
8.4.1 架构(Architecture)
有许多LSTM架构可供选择。有些体系结构适合于某些序列预测问题,尽管大多数体系结构具有足够的灵活性,可以适应您的序列预测问题,但仍要测试您对架构适用性的假设。
8.4.2 记忆单元(Memory Cells)
对于给定的序列预测问题或LSTM体系结构,我们无法知道最佳记忆单元数。必须在LSTM隐藏层中测试一组不同的存储单元,以查看最有效的方法。
- Try grid searching the numb er of memory cells by 100s, 10s, or finer.
- Try using numbers of cells quoted in research papers.
- Try randomly searching the number of cells between 1 and 1000.
常用的存储单元数如100或1000,可能是一时兴起选的。下面的例子,网格搜索第一个隐藏的LSTM层中具有少量重复(5)的存储单元1、5或10的数量。可以用这个例子作为自己实验的模板。
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# return training data
def get_train():
seq = [[0.0, 0.1], [0.1, 0.2], [0.2, 0.3], [0.3, 0.4], [0.4, 0.5]]
seq = np.array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((5, 1, 1))
return X, y
# return validation data
def get_val():
seq = [[0.5, 0.6], [0.6, 0.7], [0.7, 0.8], [0.8, 0.9], [0.9, 1.0]]
seq = np.array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((len(X), 1, 1))
return X, y
# fit an LSTM model
def fit_model(n_cells):
# define model
model = Sequential()
model.add(LSTM(n_cells, input_shape=(1,1)))
model.add(Dense(1, activation='linear'))
# compile model
model.compile(loss='mse', optimizer='adam')
# fit model
X,y = get_train()
history = model.fit(X, y, epochs=500, shuffle=False, verbose=0)
# evaluate model
valX, valY = get_val()
loss = model.evaluate(valX, valY, verbose=0)
return loss
# define scope of search
params = [1, 5, 10]
n_repeats = 5
# grid search parameter values
scores = pd.DataFrame()
for value in params:
# repeat each experiment multiple times
loss_values = list()
for i in range(n_repeats):
loss = fit_model(value)
loss_values.append(loss)
print('>%d/%d param=%f, loss=%f'% (i+1, n_repeats, value, loss))
# store results for this parameter
scores[str(value)] = loss_values
# summary statistics of results
print(scores.describe())
# box and whisker plot of results
fig = plt.figure(dpi=200)
scores.boxplot(ax = plt.gca())
plt.show()
运行该示例将打印每次迭代的搜索进度。最后显示每个memory cell 数的结果摘要统计信息。
>1/5 param=1.000000, loss=0.187934
>2/5 param=1.000000, loss=0.169736
>3/5 param=1.000000, loss=0.294507
>4/5 param=1.000000, loss=0.105454
>5/5 param=1.000000, loss=0.220867
>1/5 param=5.000000, loss=0.056324
>2/5 param=5.000000, loss=0.103125
>3/5 param=5.000000, loss=0.051873
>4/5 param=5.000000, loss=0.100868
>5/5 param=5.000000, loss=0.070574
>1/5 param=10.000000, loss=0.023056
>2/5 param=10.000000, loss=0.006242
>3/5 param=10.000000, loss=0.041770
>4/5 param=10.000000, loss=0.067101
>5/5 param=10.000000, loss=0.006736
1 5 10
count 5.000000 5.000000 5.000000
mean 0.195700 0.076553 0.028981
std 0.069417 0.024245 0.025806
min 0.105454 0.051873 0.006242
25% 0.169736 0.056324 0.006736
50% 0.187934 0.070574 0.023056
75% 0.220867 0.100868 0.041770
max 0.294507 0.103125 0.067101
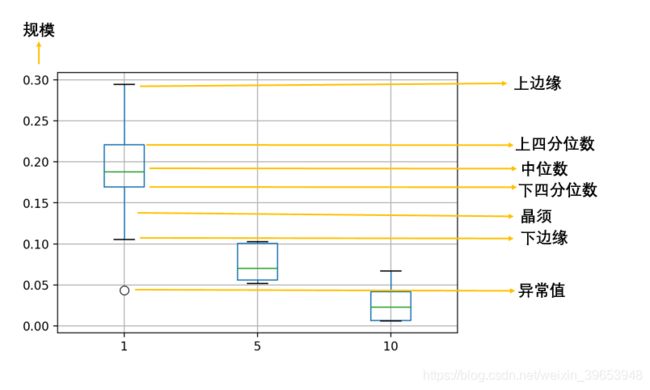
箱形图输出:
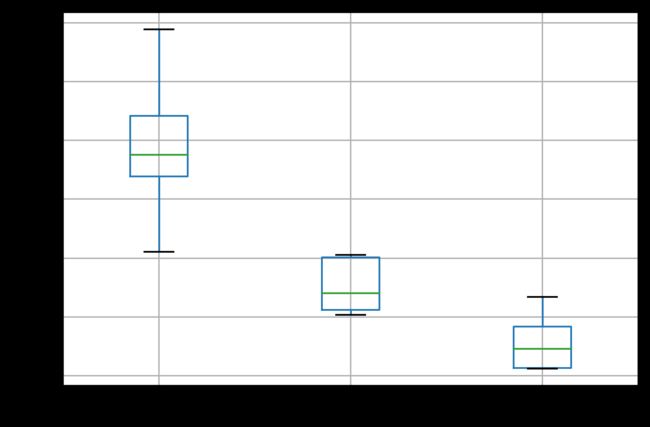
箱形图(Box-plot)又称为盒须图、盒式图或箱线图,是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。在各种领域也经常被使用,常见于品质管理。它主要用于反映原始数据分布的特征,还可以进行多组数据分布特征的比较。箱线图的绘制方法是:先找出一组数据的上边缘、下边缘、中位数和两个四分位数;然后, 连接两个四分位数画出箱体;再将上边缘和下边缘与箱体相连接,中位数在箱体中间。
主要包含六个数据节点,将一组数据从大到小排列,分别计算出他的上边缘,上四分位数Q3,中位数,下四分位数Q1,下边缘,还有一个异常值。
8.4.3 隐藏层 (Hidden Layers)
与存储单元的数量一样,对于给定的序列预测问题或LSTM体系结构,我们无法知道LSTM隐藏层的最佳数量。当有很多数据的时候,深度越深往往更好。
- 尝试网格搜索的层数和记忆单元。
- 尝试使用在研究论文中引用的堆叠LSTM层的模式。
- 尝试随机地搜索层和记忆细胞的数量。
8.4.4 权重初始化 (Weight Initialization)
默认情况下,Keras LSTM层使用glorot_uniform权重初始化。一般而言,这种权重初始化效果很好,但是在LSTM中使用普通类型的权重初始化非常成功。评估不同权重初始化方案对模型性能的影响。Keras提供了一个很好的权重初始化方案列表:
- random uniform
- random normal
- glorot uniform
- glorot normal
8.4.5 激活函数(Activation Functions)
激活函数(从技术上讲是传递函数,它传递神经元的加权激活)通常由输入或输出层的框架和比例固定。例如,LSTM对输入使用sigmoid激活函数,因此输入的比例通常为0-1。序列预测问题的分类或回归性质决定了在输出层中使用的激活函数的类型。可以尝试其他的激活函数:
- sigmoid
- tanh
- relu
此外,堆叠的LSTM中的所有LSTM层是否需要使用相同的激活函数。在实践中,很少看到模型比使用Sigmoid做得更好,但是这一假设应该得到证实。
8.5 调试学习行为
8.5.1 优化算法(Optimization Algorithm)
梯度下降的一个很好的默认实现是Adam算法。这是因为它结合了AdaGrad和RMSProp方法的最佳属性,自动为模型中的每个参数(权重)使用自定义学习率。此外,在Keras中实施Adam会对每个配置参数使用最佳初始值。也可以尝试其他优化算法:
- Adam
- RMSprop
- Adagrad
8.5.2 学习率(Learning Rate)
学习速率控制在每个批次结束时根据估计的梯度更新权重的量。这会对模型学习问题的速度或效果之间的权衡产生很大影响。考虑使用经典的随机梯度下降(SGD)优化器,探索不同的学习速率和动量值(momentum values)。不仅仅是搜索值,还可以评估改变学习率的效果。
- 网格搜索学习率(例如0.1、0.001、0.0001)。
- 尝试学习速度随时代数而衰减(例如通过callback)。
- 尝试用学习率越来越低的训练来更新拟合模型。
学习率与迭代次数(epoch,训练样本的轮数)紧密相关。一般来说,学习率越小(例如0.0001),所需的训练时间就越多。这是一个线性关系,反过来也是正确的,在较大的学习率(例如0.1)需要较少的训练时间。
8.5.3 批次大小(Batch Size)
批量大小是模型权重更新之间的样本数。一个好的默认批量大小是32个样本。
[batch_size]通常选择在1到几百之间,例如,[batch_size]=32是一个很好的默认值,大于10的值利用了矩阵-矩阵乘积比矩阵向量-乘积运算更快的原理。— Practical Recommendations For Gradient-based Training Of Deep Architectures, 2012.
序列预测问题的数据量和帧结构可能影响批量大小的选择。可以尝试一些替代配置:
- 尝试设计随机梯度下降(SGD)的批量大小为1。
- 批量大小n,其中n是批量梯度下降的样本数。
- 使用网格搜索,尝试将batch_size从2更新到256。
较大的批量通常会导致模型更快的收敛,但可能会导致最终权重集的不太理想。批处理大小为1(随机梯度下降),在每个样本之后进行更新,通常会导致学习过程波动很大。下面是用少量重复(5)对批大小1、2和3进行网格搜索的一个小示例。可以用这个例子作为自己实验的模板。
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# return training data
def get_train():
seq = [[0.0, 0.1], [0.1, 0.2], [0.2, 0.3], [0.3, 0.4], [0.4, 0.5]]
seq = np.array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((5, 1, 1))
return X, y
# return validation data
def get_val():
seq = [[0.5, 0.6], [0.6, 0.7], [0.7, 0.8], [0.8, 0.9], [0.9, 1.0]]
seq = np.array(seq)
X, y = seq[:, 0], seq[:, 1]
X = X.reshape((len(X), 1, 1))
return X, y
# fit an LSTM model
def fit_model(n_batch):
# define model
model = Sequential()
model.add(LSTM(10, input_shape=(1,1)))
model.add(Dense(1, activation='linear'))
# compile model
model.compile(loss='mse', optimizer='adam')
# fit model
X,y = get_train()
history = model.fit(X, y, epochs=500, shuffle=False, verbose=0, batch_size=n_batch)
# evaluate model
valX, valY = get_val()
loss = model.evaluate(valX, valY, verbose=0)
return loss
# define scope of search
params = [1, 2, 3]
n_repeats = 5
# grid search parameter values
scores = pd.DataFrame()
for value in params:
# repeat each experiment multiple times
loss_values = list()
for i in range(n_repeats):
loss = fit_model(value)
loss_values.append(loss)
print('>%d/%d param=%f, loss=%f'% (i+1, n_repeats, value, loss))
# store results for this parameter
scores[str(value)] = loss_values
# summary statistics of results
print(scores.describe())
# box and whisker plot of results
fig = plt.figure(dpi=200)
scores.boxplot(ax = plt.gca())
plt.show()
运行该示例将打印每次迭代的搜索进度。最后显示每个配置的结果摘要统计信息。
>1/5 param=1.000000, loss=0.001113
>2/5 param=1.000000, loss=0.003881
>3/5 param=1.000000, loss=0.001901
>4/5 param=1.000000, loss=0.001382
>5/5 param=1.000000, loss=0.001783
>1/5 param=2.000000, loss=0.000973
>2/5 param=2.000000, loss=0.000061
>3/5 param=2.000000, loss=0.001475
>4/5 param=2.000000, loss=0.000625
>5/5 param=2.000000, loss=0.001681
>1/5 param=3.000000, loss=0.002114
>2/5 param=3.000000, loss=0.001060
>3/5 param=3.000000, loss=0.000025
>4/5 param=3.000000, loss=0.004496
>5/5 param=3.000000, loss=0.001244
1 2 3
count 5.000000 5.000000 5.000000
mean 0.002012 0.000963 0.001788
std 0.001091 0.000653 0.001686
min 0.001113 0.000061 0.000025
25% 0.001382 0.000625 0.001060
50% 0.001783 0.000973 0.001244
75% 0.001901 0.001475 0.002114
max 0.003881 0.001681 0.004496
8.5.4 正则化(Regularization)
LSTMs在一些序列预测问题上可以快速收敛甚至过拟合。为了解决这个问题,可以使用正则化方法。辍学者在训练过程中随机跳过神经元,迫使层中的其他神经元选择剩余部分。它既简单又实用,使用两个不同参数可以在LSTM层上设置0.0(no dropout)到1.0(complete dropout)之间的dropout参数:
- dropout: dropout applied on input connections.
- recurrent_dropout: dropout applied to recurrent connections.
如:
model.add(LSTM(..., dropout=0.4))
LSTMs还支持其他形式的正则化,例如权重正则化减小网络权重的大小。同样,可以在LSTM层设置这些参数:
- bias_regular izer: regularization on the bias weights.
- kernel_regularizer: regularization on the input weights.
- recurrent_regularizer: regularization on the recurrent weights.
与dropout情况下的百分比不同,可以使用正则化类,如LI、L2或L1L2正则化。建议使用L1L2并使用介于0和1之间的值,这些值还允许模拟LI和L2方法。例如:
- L1L2(0.0, 0.0), e.g. baseline or no regularization
- L1L2(0.01, 0.0), e.g. L1.
- L1L2(0.0, 0.01), e.g. L2.
- L1L2(0.01, 0.01), e.g. L1L2 also called elastic net.
model.add(LSTM(..., kernel_regularizer=L1L2(0.01, 0.01)))
在实践中,在输入使用Dropout和权重正则化,可以得到性能更好的模型。
8.5.5 适时停止训练
训练阶段的数量调整可能非常耗时。另一种方法是配置大量的训练时段。然后设置检查点检查模型在训练和验证数据集上的性能,如果看起来模型开始过度学习,则停止训练。因此,适时停止是一种抑制过度拟合的规则化方法。
你可以提前在凯拉斯停留,提前回叫。它要求您指定一些配置参数,例如要监视的度量(例如val丢失)、在其上未观察到监视度量改进的时段数(例如100)。在训练模型时,会向 fit() 函数提供回调列表。例如EarlyStopping()方法:
keras.callbacks.callbacks.EarlyStopping(monitor='val_loss', min_delta=0, patience=0, verbose=0, mode='auto', baseline=None, restore_best_weights=False)
功能:当监视的变量停止改善时,停止训练。
参数:
- monitor:要监视的变量。
- min_delta:监视变量中符合改进的最小变化,即小于min_delta的绝对变化,将不视为任何改进。
- patience:产生受监控变量但没有改善的时期数,之后将停止训练。如果验证频率(model.fit(validation_freq=5))大于1 ,则可能不会为每个时期产生验证变量。
- verbose:详细模式。
- model:{自动,最小,最大}之一。在min模式下,当监视的变量停止减少时,训练将停止;在max 模式下,当监视的变量停止增加时,它将停止;在auto 模式下,将根据监视变量的名称自动推断出方向。
- baseline:要达到的监视变量的基线值。如果模型没有显示出超过基线的改善,培训将停止。
- restore_best_weights:是否从时期以受监视变量的最佳值恢复模型权重。如果为False,则使用在训练的最后一步获得的模型权重。
实例:
from keras.callbacks import EarlyStopping
es = EarlyStopping(monitor= 'val_loss', min_delta=100)
model.fit(..., callbacks=[es])
8.6 拓展阅读
-
Empirical Methods for Artificial Intelligence, 1995.
http://amzn.to/2tjlD4B -
Practical recommendations for gradient-based training of deep architectures, 2012.
https://arxiv.org/abs/1206.5533 -
Recurrent Neural Network Regularization, 2014.
https://arxiv.org/abs/1409.2329
参考:Jason Brownlee《long-short-term-memory-networks-with-python》chapter 12