【寸铁的刷题笔记】数组
寸铁的刷题笔记
大家好 我是寸铁
对最近刷过的LeetCode进行一个记录✨
喜欢的小伙伴可以点点关注
289. 生命游戏
模拟分析图
代码实现
class Solution {
public void gameOfLife(int[][] board) {
//下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的
//这句话的意思是说每个格子的状态变更只能是当前格子的状态去变更
//不能是依据格子的状态变化后的状态进行变化。
//活细胞:1 死细胞:0
//针对活细胞的规则:
// 设置活细胞 --> 死细胞的状态为2(他的原来状态也是活细胞 即1)
// 确保能把之前的活细胞统计进去
/*
1. 活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡
记录更新后的状态为2 (2 % 2 == 0)
2. 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
记录更新后的状态为3 (2 % 2 == 0)
3. 介于上面两种情况之间的,活细胞仍然存活,状态为1,不用变化。
*/
//针对死细胞的规则:
// 设置死细胞 --> 活细胞的状态为3 (他的原来状态为死细胞 即2)
/*
1. 死细胞周围正好有3个活细胞,则该位置死细胞复活。
记录更新状态为3 (3 % 2 == 1)
*/
//先把题目的各种情况分析好,再编码实现!
//编码实现
int m = board.length; //记录行数
int n = board[0].length; // 记录列数
int count = 0; // 记录统计的活细胞的个数
//枚举每个格子
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
count = 0; //针对每个格子去枚举8个方向进行计数
//上行-1、下行1、当前行0
for(int x = -1; x <= 1; x++){
//每一行的左右两个方向
for(int y = -1; y <= 1; y++){
//边界处理
//x == 0 && y == 0 相当于 (i , j) 这个点本身 ,没有任何变化 直接跳过
if((x == 0 && y == 0) || i + x < 0 || i + x >= m || j + y < 0 || j + y >= n) continue;
if(board[i + x][j + y] == 1 || board[i + x][j + y] == 2) count++;
}
}
//针对每个点各方向的格子的细胞状态进行分析
//如果是活细胞并且活细胞的个数小于2或者个数大于3则置为死细胞
if(board[i][j] == 1 && (count < 2 || count > 3)) board[i][j] = 2;
//如果是死细胞并且死细胞的个数等于3则置为活细胞
if(board[i][j] == 0 &&(count == 3))board[i][j] = 3;
}
}
//取模处理,更新细胞的状态
// 3(死细胞-->活细胞) --> 活细胞 3 % 2 = 1
// 2(活细胞 --> 死细胞) --> 死细胞 2 % 2 = 0
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
board[i][j] %= 2;
}
}
}
}
54. 螺旋矩阵
模拟分析图
代码实现
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
//先判断一下数组是否为空
if(matrix.length == 0) return new ArrayList<Integer>();
//数组下标从0开始算起
// 左边界
int l = 0;
// 右边界
int r = matrix[0].length - 1;
// 上边界
int t = 0;
// 下边界
int b = matrix.length - 1;
// 返回的答案矩阵
Integer []res = new Integer[(r + 1) * (b + 1)];
// 矩阵的变量
int x = 0;
// 不断迭代
while(true){
//从左到右
for(int i = l; i <= r; i++)res[x++] = matrix[t][i];//1 2 3
// 此时往下走
// 往下走: 一个是试探边界是否越界,一个是起到更新边界的作用,因为这时需要添加下一行的元素。
if(++t > b)break;
// 这里是在试探往下走是否越界
// 如果没越界,此时的t已经为下一行。
// 从上往下
for(int i = t; i <= b; i++)res[x++] = matrix[i][r];//1 2 3 6 9
if(l > --r)break;
// 试探往左走是否越界
// 从右到左
for(int i = r; i >= l; i--)res[x++] = matrix[b][i]; // 1 2 3 6 9 8 7
if(t > --b)break;
// 试探往上走是否越界
// 从下到上
for(int i = b; i >= t; i--)res[x++] = matrix[i][l]; // 1 2 3 6 9 8 7 4
if(++l > r) break;
// 试探往右走是否越界
}
//下一次迭代回到开头则1 2 3 6 9 8 7 4 5
//其中任何一个越界则说明到达结尾 直接break掉
return Arrays.asList(res);
}
}
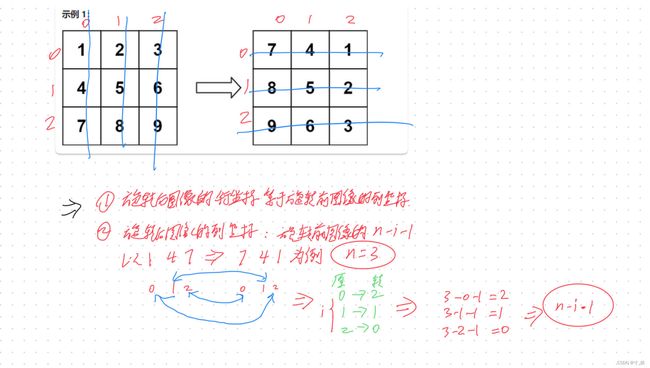
48. 旋转图像
像这种图像变化类的题目,或者是矩阵变化类的题目。
主要是观察行、列的变化规律,根据规律进行推算。
模拟分析图
代码实现
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
//记录旋转后的矩阵
int b[][] = new int[n][n];
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
//所在的列为旋转后的行
//所在的行 n - i - 1 --> 旋转后的列
b[j][n - i - 1] = matrix[i][j];
}
}
//将变化后的矩阵赋值给原矩阵
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
matrix[i][j] = b[i][j];
}
}
}
}
73. 矩阵置零
代码实现
class Solution {
public void setZeroes(int[][] a) {
int m = a.length;//行数
int n = a[0].length;//列数
boolean col[] = new boolean[m];//判断行
boolean row[] = new boolean[n];//判断列
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(a[i][j] == 0){
//设置当前元素所在的行和列都为true
col[i] = row[j] = true;
}
}
}
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
//如果说行或列为true
if(col[i] || row[j]){
//设置该行或列的所以元素为0
//在原来的a数组进行改变
a[i][j] = 0;
}
}
}
}
}
128. 最长连续序列
代码实现
class Solution {
public int longestConsecutive(int[] nums) {
//注意: 数组长度为0和数组为空时,返回0
if(nums.length == 0 || nums == null)return 0;
//序列长度至少为1
int sum = 1;//当前连续序列的长度
int lastsum = sum;//记录的是上一个连续的序列的最大长度
Arrays.sort(nums);//排序 再对连续的序列长度进行更新
for(int i = 1; i < nums.length; i++){
//当前元素和前面元素的差值为1
//则记录当前的连续长度sum
if(nums[i] - nums[i - 1] == 1){
sum++;
//每次更新sum则进行取max的操作
//求出当前最长的序列长度
lastsum = Math.max(sum,lastsum);
}else if(nums[i] - nums[i - 1] == 0){
//如果说相邻元素的差值为0
//则直接跳过 并不影响整体的结果
continue;
}else{
//相差的差值不为0或1
//则说明断层了
//此时,序列不连续,sum为1即它本身
sum = 1;
}
}
return lastsum;
}
}
56. 合并区间
模拟分析图
代码实现
class Solution {
public int[][] merge(int[][]a) {
List<int []> res = new ArrayList<>();
//对区间进行排序
//先按x[0]排序
//x[0]相等则按y[0]排序
Arrays.sort(a,(x,y) -> x[0] - y[0]);
int l = a[0][0];//左边界
int r = a[0][1];//右边界
//情况1:区间1的右边比区间2的左边要大
//这时说明区间1包含部分区间2
//左边界不用变,右边界取最值
//情况2:区间1的右边等于区间2的左边
//此时,区间1已经包含了这个相等的数,所以直接选右边界的最大值即可
//上述两种情况可以合并着写
//情况3:
//区间1的右边小于区间2的左边
//这时,无法合并区间,创建一个点对去存区间2即可
for(int i = 1; i < a.length; i++){
if(a[i][0] > r){
//如果说满足情况3则把之前更新的l和r添加到res中
//即将前一个区间 [l, r] 加入结果列表
//再更新左右边界为当前区间的起始位置和终止位置。
res.add(new int[]{l,r});
l = a[i][0];
r = a[i][1];
}else{
//更新右边界,此时不用合并,看能不能找到更大的右边界
//直到情况3时,再把区间合并。
r = Math.max(r , a[i][1]);
}
}
//处理最后一个待合并的区间
res.add(new int[]{l,r});
//将list转换为二维数组返回
return res.toArray(new int[0][]);
}
}
看到这里的小伙伴,恭喜你又掌握了一个技能
希望大家能取得胜利,坚持就是胜利
我是寸铁!我们下期再见
往期好文
保姆级教程
【保姆级教程】Windows11下go-zero的etcd安装与初步使用
【保姆级教程】Windows11安装go-zero代码生成工具goctl、protoc、go-zero
【Go-Zero】手把手带你在goland中创建api文件并设置高亮
报错解决
【Go-Zero】Error: user.api 27:9 syntax error: expected ‘:‘ | ‘IDENT‘ | ‘INT‘, got ‘(‘ 报错解决方案及api路由注意事项
【Go-Zero】Error: only one service expected goctl一键转换生成rpc服务错误解决方案
【Go-Zero】【error】 failed to initialize database, got error Error 1045 (28000):报错解决方案
【Go-Zero】Error 1045 (28000): Access denied for user ‘root‘@‘localhost‘ (using password: YES)报错解决方案
【Go-Zero】type mismatch for field “Auth.AccessSecret“, expect “string“, actual “number“报错解决方案
【Go-Zero】Error: user.api 30:2 syntax error: expected ‘)‘ | ‘KEY‘, got ‘IDENT‘报错解决方案
【Go-Zero】Windows启动rpc服务报错panic:context deadline exceeded解决方案
Go面试向
【Go面试向】defer与time.sleep初探
【Go面试向】defer与return的执行顺序初探
【Go面试向】Go程序的执行顺序
【Go面试向】rune和byte类型的认识与使用
【Go面试向】实现map稳定的有序遍历的方式