希尔排序和归并排序详解

目录

希尔排序

归并排序

希尔排序

希尔排序又称缩小增量排序

希尔排序是直接插入排序的优化版本.但又不同于直接插入排序，下面来先详细介绍它.

基本思想：

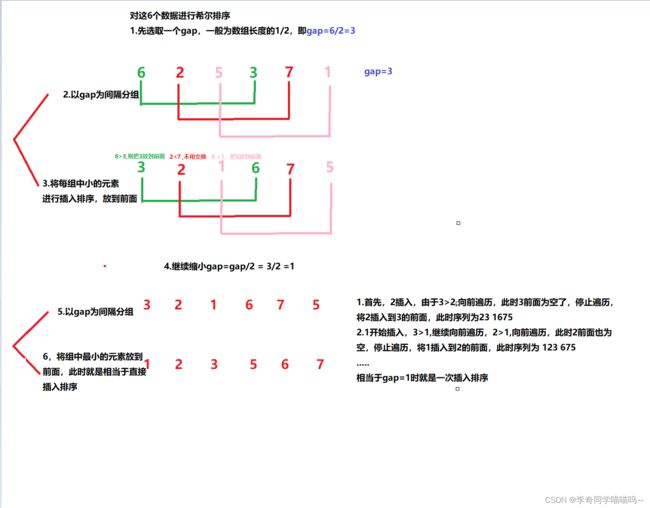
1.先选定一个小于n的数为gap，先从第一个元素开始，将所有距离为gap的数分为一组，进行直接插入排序.

2.再选定一个小于gap的数字，继续分组、插入排序，即重复1的操作

3.当gap=1时，相当于整个数组就是一组，再次进行插入排序即整体有序.

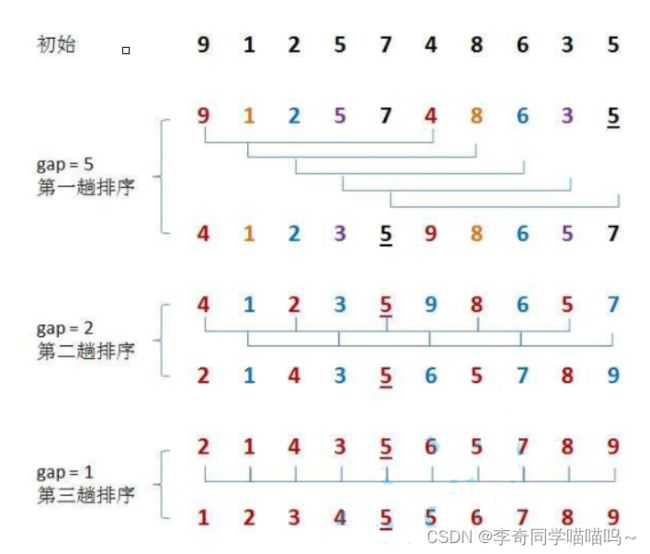
可以看如下动图理解一下：

 动图来源于网络.

我们画图来继续理解它的具体过程和实现.

 或者下面的图片：

这样过程基本就差不多说清楚了. 

可能有的同学会有问题，就是分组前面排了那么多次序,但是最后一次还是插入排序

我直接用插入排序不就可以了吗，还那么复杂做什么呢？

其实每次gap分组预处理，都是使数组里的数字接近有序，每次排完都会发现，越来越多较小的数字都会被排在数组的前面的部分.这样最后一次插入排序的效率会相较于什么都不做处理的插入排序效率提高不少.所以先进行预处理，再进行插入排序效率会更高.

其中：gap越大，预排速度越快，但不接近于有序.

gap越小，预排速度越慢，但越接近于有序.

所以代码如下：

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;//选取一个gap，比gap小即可，但是最好是除以3
		//相当于插入排序，只不过由之前直接插入排序的间隔为1改成了间隔为gap.
        for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int x = a[end+gap];
			while (end >= 0)
			{
				if (x < a[end])
				{
					a[end+gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = x;
		}
	}
}

归并排序

基本思想：先分解，再合并.采用的算法思想是分治思想.

我们先将数组分解成子序列，再将子序列继续分解，直至不能再被分解

最后再合并，并使之有序，不停的归并，然后就会得到一个排序好的序列.

先来看动图：

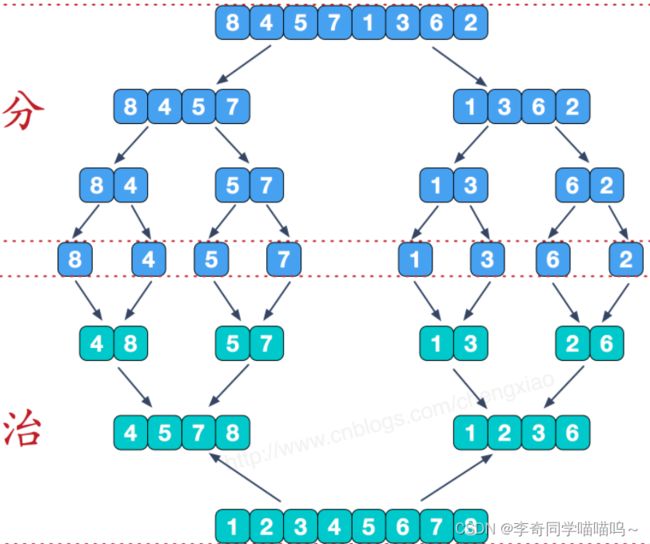
这个只体现了分治过程中“治”的过程. 即只体现了分解好之后的归并，没有体现分解，那么用下面一张图来体现分解和归并。

意思是，你可以用下面那张图理解分解过程，利用上面动图来理解归并过程.

 这个看起来是不是有些像二叉树，所以我们可以使用递归的方法来解决.

代码如下：

void MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
	{
		return;
	}
	int mid = (begin + end) / 2;
	//[begin,mid],[mid+1,end]
	MergeSort(a, begin, mid, tmp);
	MergeSort(a, mid + 1, end, tmp);
	//经过上面两次递归，此时已经分解完毕.
	
	//归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin1;
	while (begin1 <= mid && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	//每次将归并到tmp里的内容拷贝回a数组里.
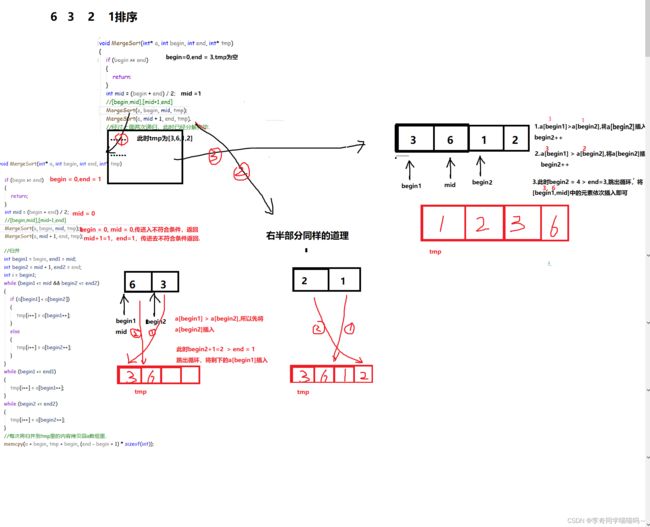
	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}

我把程序运行的图画一下，方便大家理解.

非递归版本：

//归并排序(非递归)
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("Malloc fail\n");
		exit(-1);
	}
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			//[i,i+gap-1][i+gap,i+2*gap-1]
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}
			int j = begin1;
			int m = end2 - begin1 + 1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			memcpy(a + i, tmp + i, sizeof(int) * m);
		}
		gap *= 2;
	} 
}

这就是希尔排序和堆排序的全部内容了。如果有需要补充或错误的地方，欢迎补充或指正哦