Splay

定义

Splay是一颗平衡二叉树，但是往往没那么平衡，期望高度是$log(n)$

应用

不仅支持普通平衡树的操作，包括一些区间问题(一般用线段树解决)的也支持；

保证高度的思想

对某个结点进行操作的时候，将其旋转到树根；

这里的操作指的是像插入，查询等等；

也就是说，这跟操作系统的局部性原理类似，某个点既然当前用到了，那么后续肯定还会用到；

拉到根结点其实就是进行了一个类似缓存的操作；

---

应用这个思想，就能保证平均意义下，一次操作的时间复杂度是$O(logn)$级别的；

那么这个操作如何实现呢？见下方的Splay操作；

基本操作

查询x的排名

查询前驱

查询后继

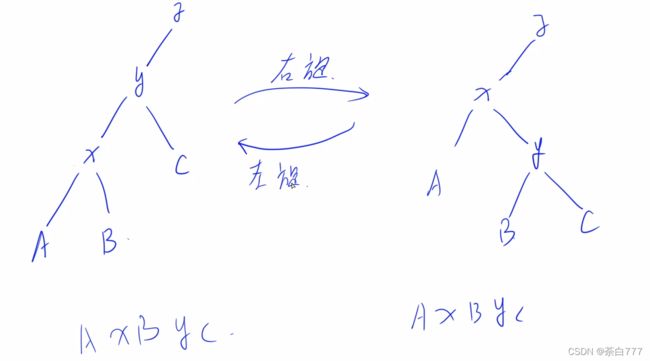
左右旋转

和其他的平衡树一样，保持中序遍历不变，改变高度；

Splay操作

Splay(x,k)表示将$x$旋转到$k$的下面；

当$k=0$时，$x$就变成根了；

分为两大类（对称的情况同理)

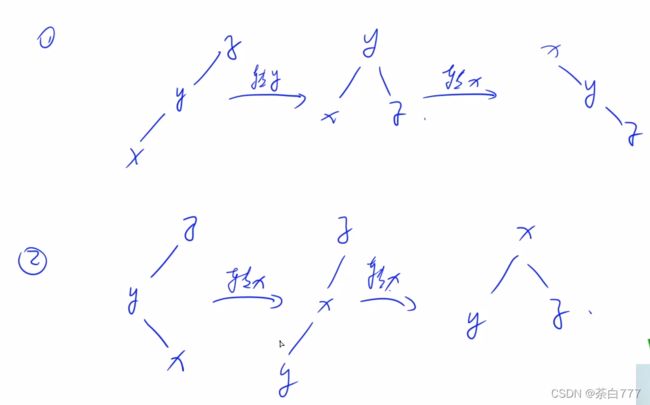
可以发现每操作一次，$x$的高度就+2，不断的迭代直到父节点为$k$；

一般来说，$k$只会取$0$，以及根结点这两种情况；

插入一段序列

比如说我们要将某个序列插入$y$的后面，在中序遍历中，$y$的后继是$z$；

1. $Splay(y,0)$
2. $Splay(z,y)$
3. 将整个序列构造成一棵二叉树插入$z$的左子树；

因为$z$是$y$的后继，那么其左子树必然为空(不然不符合中序遍历)

建树

偷懒的方法，就直接搞成一条链(特殊的Splay，但是效率低)

常规的方法，取中点设为rt，然后递归建立左右区间；

删除一段序列

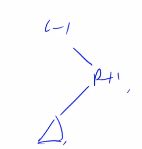
假设要删除$[L,R]$这一段；

找到$L$的前驱$L-1$，找到$R$的后继$R+1$；

1. $Splay(L-1,0)$
2. $Splay(R+1,L-1)$
3. 删去$R+1$的左子树(变成NULL即可)；

旋转前两步以后，$[L,R]$就是$R+1$的左子树了；

push_up

和线段树类似，用子节点的信息来维护父节点；

当旋转的时候使用；

push_down

和线段树类似，传递懒标记；

当访问子节点的时候使用；

合并两颗Splay

注意要求，$x$树的最大值小于$y$树的最小值；

其实就是按照BST的规则插入；

其他操作

其他操作就和普通的平衡树一样；

注意

Splay是一颗BST，但是要时刻注意排序的关键字是什么；

如果仅仅涉及仅仅涉及到旋转、插入节点、删除节点、分裂树、合并树这些操作是符合常规BST的；

但对于我们的例题一Splay来说，此时排序的关键字是序列下标，那么对于序列中元素的值就不一定满足BST性质了；

---

Splay时时刻刻保证中序遍历是当前序列的顺序，但是并不能保证是有序的；

---

一般来说，涉及删除操作，我们通常会加入两个哨兵；

当删除的时候，一般会取前一个点和后一个点；

那么加入哨兵就可以防止越界了；

例题

Splay

传送门

题面

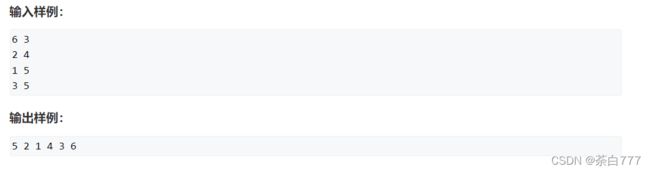
思路

这题Splay的用法类似于线段树，我们维护的是一个序列（不一定有序）；

维护信息
   1.子树总点数  size 用于递归查找位置
   2.懒标记     flag 整个区间是否需要翻转
其他操作上面已经提到了，或者就是常规平衡树写法；

Code

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;
int root,tot,n,m;
struct Node{
	int s[2];//左右儿子
	//注意这个val不是一般平衡树的val
	int val,fa;//值、父节点
	int sz,flag;//点的个数，该区间是否反转
	void init(int _val,int _fa){
		val = _val,fa = _fa;
		sz = 1;
		s[0] = s[1] = flag = 0;
	}
}tr[N];
#define lc (tr[p].s[0])
#define rc (tr[p].s[1])
void push_up(int p){
	//注意这里要 + 1
	tr[p].sz = 1 + tr[lc].sz + tr[rc].sz;
}
void push_down(int p){
	if(tr[p].flag){
		swap(lc,rc);
		tr[lc].flag ^= 1;
		tr[rc].flag ^= 1;
		tr[p].flag = 0;
	}
}
//旋转x(自适应左旋、右旋)
//注意，旋转x意味着把x往上提
void rotate(int x){
	int y = tr[x].fa,z = tr[y].fa;
	//k = 0 x为左儿子；k = 1，x为右儿子
	int k = tr[y].s[1] == x;
	//旋转
	tr[z].s[tr[z].s[1] == y] = x,tr[x].fa = z;
	tr[y].s[k] = tr[x].s[k^1],tr[tr[x].s[k^1]].fa = y;
	tr[x].s[k^1] = y,tr[y].fa = x;
	//注意此时y是x儿子，因此先push_up y
	push_up(y);
	push_up(x);
}
//将x转到k下面
void splay(int x,int k){
	while(tr[x].fa != k){
		int y = tr[x].fa,z = tr[y].fa;
		if(z != k){//先转一次
			//如果是折线形
			if((tr[y].s[1] == x) ^ (tr[z].s[1] == y))
				rotate(x);
			//如果是直线形
			else
				rotate(y);	
		}
		//再转一次
		rotate(x);
	}
	if(!k) root = x;
}
void insert(int val){
	int u = root,fa = 0;
	while(u){
		fa = u;
		//看看插哪
		u = tr[u].s[val > tr[u].val];
	}
	u = ++tot;
	if(fa)
		tr[fa].s[val > tr[fa].val] = u;
	tr[u].init(val,fa);
	splay(u,0);//缓存操作
}
//找中序遍历的第k大
int kth(int p,int k){
	push_down(p);
	if(tr[lc].sz >= k) return kth(lc,k);
	else if(tr[lc].sz + 1 == k) return p;
	else return kth(rc,k - 1 - tr[lc].sz);
}
//中序遍历
void infix_order(int p){
	push_down(p);
	if(lc) infix_order(lc); 
	//不要输出哨兵
	if(tr[p].val >= 1 && tr[p].val <= n)
		cout << tr[p].val << ' ';
	if(rc) infix_order(rc);
}
void solve(){
	cin >> n >> m;
	for(int i=0;i<=n+1;++i) insert(i);
	while(m--){
		int l,r;
		cin >> l >> r;
		//第l + 1 - 1 个数
		int pre = kth(root,l);
		//第r + 1 + 1 个数
		int nxt = kth(root,r + 2);
		//将L - 1 转到根
		splay(pre,0);
		//将R + 1 转到L - 1 下面
		splay(nxt,pre);
		//需要翻转的区间在R + 1 的左子树
		tr[tr[nxt].s[0]].flag ^= 1;
	}
	infix_order(root);
}

signed main(){
	std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	solve();
	return 0;
}

郁闷的出纳员

传送门

题面

思路

这题跟上题不同，这题Splay维护的类似传统平衡树；

维护的是一个有序的序列；

---

题目要求以下几种操作；

• 插入
• 集体涨薪
• 集体降薪
• 剩余员工中找第k大

因为降薪后某些员工会离职，因此我们还需要支持区间删除这个操作；

---

因为涨薪和降薪都是集体的，因此我们维护一个偏移量offset即可；

每个员工的工资则为salary + offset；

离职的问题，我们可以找到某个员工的工资恰好满足salary + offset ≥ min_salary；

然后引入两个哨兵放在开头和结尾；

然后直接进行区间删除即可，上面有提到；

Code

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;
int idx,root;
struct Node{
	int s[2],fa,val;
	int sz;//需要找第k大
	void init(int _fa,int _v){
		fa = _fa;
		val = _v;
		sz = 1;
	}
}tr[N];

#define lc (tr[p].s[0])
#define rc (tr[p].s[1])
int push_up(int p){
	tr[p].sz = 1 + tr[lc].sz + tr[rc].sz;
}
void rotate(int x){
	int y = tr[x].fa,z = tr[y].fa;
	int k = tr[y].s[1] == x;
	tr[z].s[tr[z].s[1] == y] = x,tr[x].fa = z;
	tr[y].s[k] = tr[x].s[k^1],tr[tr[x].s[k^1]].fa = y;
	tr[x].s[k^1]=y,tr[y].fa = x;
	push_up(y),push_up(x);
}
//把x转到k下面
void splay(int x,int k){
	while(tr[x].fa != k){
		int y = tr[x].fa,z = tr[y].fa;
		//先转一次
		if(z != k){
			//如果是折线
			if((tr[z].s[1] == y) ^ (tr[y].s[1] == x)){
				rotate(x);
			}
			//如果是直线
			else rotate(y);
		}
		rotate(x);
	}
	if(!k) root = x;
}
int n,mn,offset;
int insert(int val){
	int u = root,fa = 0;
	while(u){
		fa = u;
		u = tr[u].s[val > tr[u].val]; 
	}
	u = ++idx;
	if(fa){
		int k = val > tr[fa].val;
		tr[fa].s[k] = u;
	}
	tr[u].init(fa,val);
	splay(u,0);
	return u;
}
//找到第一个大于等于val的
int find(int val){
	int u = root,fa = 0;
	int ret = 0;
	while(u){
		if(tr[u].val >= val){
			ret = u;//u可能是答案
			u = tr[u].s[0];//去左树，如果左树是空的，那么自然是父节点
		}
		else u = tr[u].s[1];
	}
	return ret;
}
//排名第k大的工资
int kth(int p,int k){
	if(tr[rc].sz >= k) return kth(rc,k);
	else if(tr[rc].sz + 1 == k) return tr[p].val;
	else{
		return kth(lc,k - 1 - tr[rc].sz);
	}
}
void solve(){
	int first = insert(-1e9),last = insert(1e9);
	cin >> n >> mn;
	int cnt = 0;
	while(n--){
		char opt;
		int x;
		cin >> opt >> x;
		if(opt == 'I'){
			if(x < mn) continue;
			++cnt;
			//真实工资为 salary + offset
			int salary = x - offset;
			insert(salary);
		}
		else if(opt == 'A'){
			offset += x;
		}
		else if(opt == 'S'){
			offset -= x;
			//找到第一个工资恰好>=mn的位置
			int R = find(mn - offset);
			//删除[first+1,R-1]
			splay(R,0);
			splay(first,R);
			tr[first].s[1] = 0;
			push_up(first);//first在R下面 先push_up(first)
			push_up(R);
		}
		else{
			if(tr[root].sz - 2 < x){
				cout << -1 << '\n';
			}
			else{
				cout << kth(root,x+1) + offset << '\n';
			}
		}
	}
	//一共进来cnt个，现在剩下tr[root].sz - 2 个
	int ans = cnt - (tr[root].sz - 2);
	cout << ans << '\n';
}

signed main(){
	std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	solve();
	return 0;
}

永无乡

传送门

题面

思路

这题的Splay是按照重要程度为排序关键字；

---

题目要求我们支持两种操作；

• 合并两个集合
• 动态查询某个集合中第$k$小

合并集合的话，我们可以考虑使用并查集来完成；

第$k$小我们可以考虑使用Splay来完成；

但是如果暴力合并所有的Splay，时间复杂度是$O(n^{2}logn)$的；

这里有一个常用的技巧——启发式合并（按秩合并）

我们每次都将小的集合合并到大的集合中；

合并Splay树也按这个顺序，时间复杂度就可以优化到$O(nlo{g}^{2}n)$

启发式合并的时间复杂度是$O(nlogn)$，然后我们插入操作是$O(logn)$；

---

合并过程也很暴力，遍历某棵被合并树，然后将其上面的结点一个个insert到目标树；

Code

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int M = 5e5 + 10,N = M + M * 6;//n + nlogn个点 nlogn是启发式合并的上限

struct Node{
	int s[2],fa,val,id;//排序关键字为val,因此要存一个id
	int sz;
	void init(int v,int _id,int _fa){
		val = v,id = _id,fa = _fa;
		sz = 1;
		s[0] = s[1] = 0;
	}
}tr[N];
#define lc (tr[p].s[0])
#define rc (tr[p].s[1])
int root[N],p[N];//root(i)表示编号i所在的Splay的根
int find(int x){
	if(x == p[x]) return x;
	return p[x] = find(p[x]);
}
void push_up(int p){
	tr[p].sz = 1 + tr[rc].sz + tr[lc].sz;
}
void rotate(int x){
	int y = tr[x].fa,z = tr[y].fa;
	int k = tr[y].s[1] == x;
	tr[z].s[tr[z].s[1] == y] = x,tr[x].fa = z;
	tr[y].s[k] = tr[x].s[k^1],tr[tr[x].s[k^1]].fa = y;
	tr[x].s[k^1] = y,tr[y].fa = x;
	push_up(y),push_up(x);
}
void splay(int x,int k,int idx){
	while(tr[x].fa != k){
		int y = tr[x].fa,z = tr[y].fa;
		if(z != k){
			if((tr[y].s[1] == x) ^ (tr[z].s[1] == y)){
				rotate(x);
			}
			else rotate(y);
		}
		rotate(x);
	}
	if(!k) root[idx] = x;
}
int tot;
//将值为val，编号为id的数 插入根为root[idx]的Splay
void insert(int val,int id,int idx){
	int u = root[idx],fa = 0;
	while(u){
		fa = u;
		u = tr[u].s[val > tr[u].val];
	}
	u = ++tot;
	if(fa){
		tr[fa].s[val > tr[fa].val] = u;
	}
	tr[u].init(val,id,fa);
	splay(u,0,idx);
}
//将结点p合并到根为root[idx]的Splay中
void dfs(int p,int idx){
	if(!p) return;
	insert(tr[p].val,tr[p].id,idx);
	dfs(lc,idx),dfs(rc,idx);
}
void merge(int u,int v){
	int fu = find(u),fv = find(v);
	if(fu == fv) return;
	if(tr[root[fu]].sz > tr[root[fv]].sz) swap(fu,fv);
	dfs(root[fu],fv);
	p[fu] = fv;
}
//在根为p的Splay中，找第k小的数的编号
int kth(int k,int p){
	if(tr[lc].sz >= k) return kth(k,lc);
	else if(tr[lc].sz + 1 == k) return tr[p].id;
	else return kth(k - 1 - tr[lc].sz,rc);
}
void solve(){
	int n,m;
	cin >> n >> m;
	for(int i=1;i<=n;++i){
		root[i] = p[i] = i;
		int val;
		cin >> val;
		tr[++tot].init(val,i,0);
	}
	while(m--){
		int u,v;
		cin >> u >> v;
		merge(u,v);
	}
	int q = 0;
	cin >> q;
	while(q--){
		char opt;
		int x,y;
		cin >> opt >> x >> y;
		if(opt == 'B'){
			merge(x,y);
		}
		else{
			int fx = find(x);
			if(tr[root[fx]].sz < y) cout << -1 << '\n';
			else cout << kth(y,root[fx]) << '\n';
		}
	}
}

signed main(){
	std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	solve();
	return 0;
}

维护数列

传送门

题面

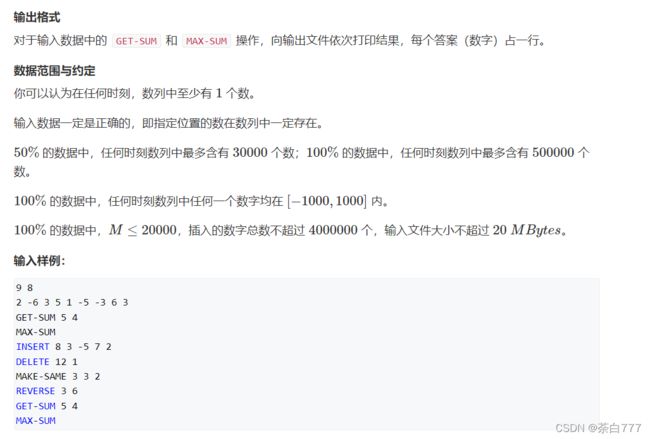
思路

这题我们的排序关键字是下标，也就是不维护一个有序序列；

• 区间修改，那么需要一个懒标记cover；
• 区间翻转，那么需要一个懒标记rev；
• 区间求和，那么需要维护一个sum来表示；
• 最大子段和，类似线段树；维护最长前缀ls，最长后缀rs，最大子段和ms；
• 插入、删除；那么需要找第$k$个元素；也就是说需要维护一个元素个数sz；

---

注意这里有一个需要注意的点；

当打上懒标记以后，我们维护的是修改后的值；

为什么上面的例题Splay不需要呢？

那题虽然也有一个翻转懒标记，但是翻转以后并不影响另一个信息sz的值；

但是这题不同，你翻转了以后，甚至区间修改了以后；

ls,rs,ms,sum可能都会改变的；

因此我们需要规定好；

---

因为题目没有明确说明最多可能存在的点；

为了防止MLE，我们考虑时间换空间；

引入内存回收，也就是搞一个数组，存可以分配的位置；

每当删除的时候，我们就把这整段放入这个回收数组；

当然TLE的话还是空间换时间吧

Code

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 5e5 + 10;

const int INF = 1e9;

struct Node{
	int s[2],fa,val;
	int cover,rev;
	int sum,ls,rs,ms;
	int sz;
	void init(int _p,int _v){
		fa = _p,val = _v;
		s[0] = s[1] = 0;
		cover = rev = 0;
		sz = 1;
		sum = ms = _v;
		ls = rs = max(_v,0);
	}
}tr[N];
#define lc (tr[p].s[0])
#define rc (tr[p].s[1])
int root;
void push_up(int);
void rotate(int x){
	int y = tr[x].fa,z = tr[y].fa;
	int k = tr[y].s[1] == x;
	tr[z].s[tr[z].s[1] == y] = x,tr[x].fa = z;
	tr[y].s[k] = tr[x].s[k^1],tr[tr[x].s[k^1]].fa = y;
	tr[x].s[k^1] = y,tr[y].fa = x;
	push_up(y),push_up(x);
}
void push_down(int);
void splay(int x,int k){
	while(tr[x].fa != k){
		int y = tr[x].fa,z = tr[y].fa;
		if(z != k){
			if((tr[y].s[1] == x) ^ (tr[z].s[1] == y))
				rotate(x);
			else rotate(y);
		}
		rotate(x);
	}
	if(!k) root = x;
}
void push_up(int p){
	tr[p].sz = tr[lc].sz + tr[rc].sz + 1;
	tr[p].sum = tr[lc].sum + tr[rc].sum + tr[p].val;
	tr[p].ls = max(tr[lc].ls,tr[lc].sum + tr[p].val + tr[rc].ls);
	tr[p].rs = max(tr[rc].rs,tr[rc].sum + tr[p].val + tr[lc].rs);
	tr[p].ms = max({tr[lc].ms,tr[rc].ms,tr[lc].rs+tr[p].val+tr[rc].ls});
}
void push_down(int p){
	if(tr[p].cover){
		//全部变成一个数，反转无所谓了；
		tr[p].cover = tr[p].rev = 0;
		int v = tr[p].val;
		auto &ls = tr[lc],&rs = tr[rc];
		if(lc){
			 ls.cover = 1;
			 ls.rev = 0;
			 ls.val = v;
			 ls.sum = tr[lc].sz * v;
		}
		if(rc){
			 rs.cover = 1;
			 rs.rev = 0;
			 rs.val = v;
			 rs.sum = rs.sz * v;
		}
		if(v > 0){
			if(lc) ls.ms = ls.ls = ls.rs = ls.sum;
			if(rc) rs.ms = rs.ls = rs.rs = rs.sum;
		}
		else{
			if(lc) ls.ms = v,ls.ls = ls.rs = 0;
			if(rc) rs.ms = v,rs.ls = rs.rs = 0;
		}
	}
	else if(tr[p].rev){
		tr[lc].rev ^= 1;
		tr[rc].rev ^= 1;
		swap(tr[lc].s[0],tr[lc].s[1]);
		swap(tr[lc].ls,tr[lc].rs);
		swap(tr[rc].s[0],tr[rc].s[1]);
		swap(tr[rc].ls,tr[rc].rs);
		tr[p].rev = 0;
	}
}
int kth(int p,int k){
	push_down(p);
	if(tr[lc].sz >= k) return kth(lc,k);
	else if(tr[lc].sz + 1 == k) return p;
	else return kth(rc,k - 1 - tr[lc].sz);
}
int recycle[N],tt;//回收机制
int get_idx(){
	return recycle[tt--];
}
int w[N];
int build(int fa,int l,int r){
	int mid = (l + r) >> 1;
	int u = get_idx();
	tr[u].init(fa,w[mid]);
	//如果有左儿子
	if(l < mid) tr[u].s[0] = build(u,l,mid-1);
	//如果有右儿子
	if(mid < r) tr[u].s[1] = build(u,mid+1,r);
	push_up(u);
	return u;
}
//回收整棵树
void dfs(int p){
	recycle[++tt] = p;
	if(lc) dfs(lc);
	if(rc) dfs(rc);
}
void solve(){
	//0号点不能用，表示null或初始父节点
	for(int i=1;i<N;++i) recycle[++tt] = i;
	int n,m;
	cin >> n >> m;
	//val、ms可能是负数，ls、rs、sum最小都是0
	w[0] = w[n+1] = tr[0].ms = tr[n+1].ms = -INF;
	for(int i=1;i<=n;++i) cin >> w[i];
	root = build(0,0,n+1);//0,n+1是哨兵,防止越界
	string cmd;
	int pos,tot,val;
	while(m--){
		cin >> cmd;
		if(cmd == "INSERT"){
			cin >> pos >> tot;
			for(int i=1;i<=tot;++i){
				cin >> w[i];
			}
			//注意哨兵
			int L = kth(root,1+pos);
			int R = kth(root,2+pos);
			splay(R,0);
			splay(L,R);
			int u = build(L,1,tot);
			tr[L].s[1] = u;
			push_up(L),push_up(R);
		}
		else if(cmd == "DELETE"){
			cin >> pos >> tot;
			int L = kth(root,pos);
			int R = kth(root,pos+tot+1);
			splay(R,0);
			splay(L,R);
			dfs(tr[L].s[1]);
			tr[L].s[1] = 0;
			push_up(L),push_up(R);
		}
		else if(cmd == "MAKE-SAME"){
			cin >> pos >> tot >> val;
			int L = kth(root,pos);
			int R = kth(root,pos+tot+1);
			splay(R,0);
			splay(L,R);
			auto &tar = tr[tr[L].s[1]];
			tar.cover = 1;
			tar.val = val;
			tar.sum = tar.sz * val;
			if(val > 0){
				tar.ms = tar.ls = tar.rs = tar.sum;
			}
			else{
				tar.ls = tar.rs = 0;
				tar.ms = val;
			}
			push_up(L),push_up(R);
		}
		else if(cmd == "REVERSE"){
			cin >> pos >> tot;
			int L = kth(root,pos);
			int R = kth(root,pos+tot+1);
			splay(R,0);
			splay(L,R);
			auto &tar = tr[tr[L].s[1]];
			tar.rev ^= 1;
			swap(tar.ls,tar.rs);
			swap(tar.s[0],tar.s[1]);
			push_up(L),push_up(R);
		}
		else if(cmd == "GET-SUM"){
			cin >> pos >> tot;
			int L = kth(root,pos);
			int R = kth(root,pos+tot+1);
			splay(R,0);
			splay(L,R);
			auto &tar = tr[tr[L].s[1]];
			cout << tar.sum << '\n';
		}
		else{
			cout << tr[root].ms << '\n';
		}
	}
}

signed main(){
	std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	solve();
	return 0;
}

注意

代码中没有在rotate和splay函数中push_down，是因为我们在进行rotate和splay之前的kth中已经下传标记了；

总结

Splay既可以像线段树一样维护序列，也可以像普通平衡树一样维护有序序列；

维护有序序列的排序关键字是val，而维护序列的排序关键字则是下标；

很容易理解，因为Splay总是维护一个合法的中序遍历；

维护有序序列的时候，中序遍历自然就是排好序的；

而维护下标的时候，其实就跟线段树一样，中序遍历是一段连续的区间；

---

当更新完子节点，记得push_up；

当访问子节点的时候，记得push_down；

---

Splay维护区间信息都是这么个流程；

比如我们要搞$[L+1,R-1]$，那么找到$L$，$R$；

将$L$搞到根，将$R$变成$L$的右儿子；

然后区间$[L+1,R-1]$就在$R$的左儿子了；

当然你也可以对称的搞，将$R$放到根，$L$放到$R$的左子树，那么区间$[L+1,R-1]$就在$L$的右子树了；

参考

• Acwing
• OI-WiKi