Leetcode 77 组合
1.题目描述
给定两个整数
n和k，返回范围[1, n]中所有可能的k个数的组合。你可以按 任何顺序 返回答案。
输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
1 <= n <= 20
1 <= k <= n
2.思路分析
- 回溯法解决的经典问题之一
- 回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了。
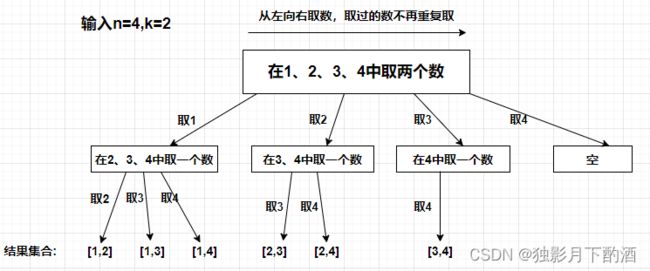
可以看出这个棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不在重复取。
第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。
每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。
图中可以发现n相当于树的宽度，k相当于树的深度。 每次搜索到了叶子节点即为结果
步骤:
-
递归函数的返回值以及参数
定义两个全局变量( 一个存放符合条件单一结果，一个存放符合条件结果的集合)
res=[] #存放符合条件结果的集合 path=[] #用来存放符合条件结果int型变量 startIndex( 记录本层递归的中，集合从哪里开始遍历(集合就是[1,…,n] ) )
每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex。
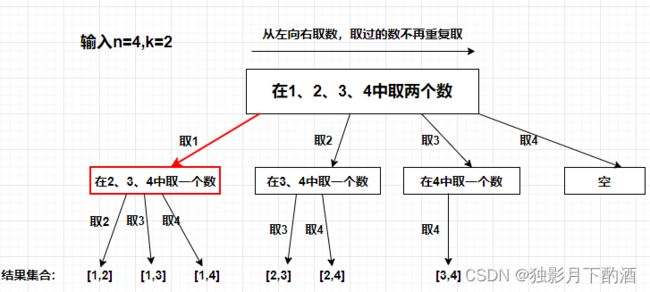
从图中的红线可以看出, 在集合[1,2,3,4]取1之后，下一层递归，就要在[2,3,4]中取数了，那么下一层递归如何知道从[2,3,4]中取数呢，靠的是startIndex。
startIndex: 记录下一层递归，搜索的起始位置。
def backtrack(n:int, k:int, StartIndex:int):
-
回溯函数终止条件
什么时候到达所谓的叶子节点了呢？
path数组的大小如果达到k，说明找到了一个子集大小为k的组合了，在图中path存的就是根节点到叶子节点的路径。
用result二维数组，把path保存起来，并终止本层递归。
if len(path) == k: res.append(path[:]) return -
单层搜索的过程
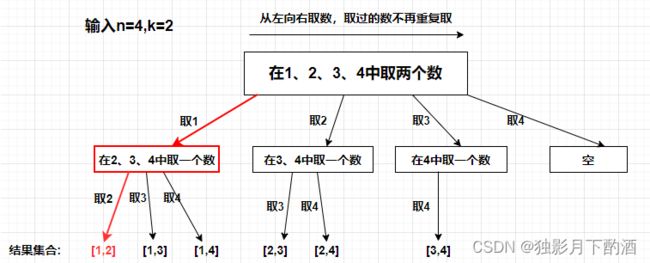
回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。
for循环每次从startIndex开始遍历，然后用path保存取到的节点i。
for i in range(StartIndex, n + 1):# 控制树的横向遍历
path.append(i) # 处理节点
backtrack(n, k, i+1) # 递归:控制纵向遍历,注意下一层的搜索从i+1开始
path.pop() # 回溯,撤销处理节点
回溯模板
def backtracking(参数) {
if (终止条件) {
存放结果
return
}
for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
处理节点;
backtracking(路径，选择列表) // 递归
回溯，撤销处理结果
}
}
3.代码实现
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res = [] # 存储符合条件结果的集合
path = [] # 用来存放符合条件的结果
def backtrack(n, k, StartIndex):
if len(path) == k:
res.append(path[:])
return
for i in range(StartIndex, n + 1):
path.append(i) # 处理节点
backtrack(n, k, i+1) # 递归,注意下层搜索从i+1开始
path.pop() # 回溯,撤销处理节点
backtrack(n, k, 1)
return res
4.剪枝优化
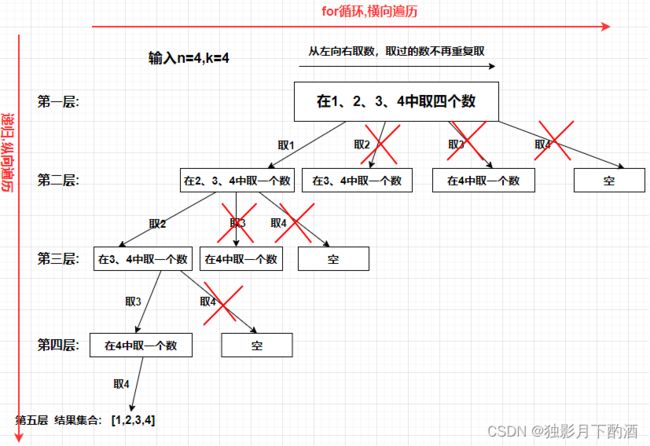
举个栗子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。
图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。
可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。
# 优化前
for i in range(StartIndex, n + 1):
# 优化后
for i in range(startIndex,n-(k-len(path))+2):
- 已经选择的元素个数：path.size();
- 还需要的元素个数为: k - path.size();
- 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历,+1(包含起始位置)
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res=[] #存放符合条件结果的集合
path=[] #用来存放符合条件结果
def backtrack(n,k,startIndex):
if len(path) == k:
res.append(path[:])
return
for i in range(startIndex,n-(k-len(path))+2): #优化的地方
path.append(i) #处理节点
backtrack(n,k,i+1) #递归
path.pop() #回溯，撤销处理的节点
backtrack(n,k,1)
return res
5.总结
- 组合问题回溯法解决的经典问题
- 明确回溯三部曲:回溯函数要处理的参数以及返回值、回溯终止条件、单层搜索逻辑
- 画图思路更加清晰