【力扣每日一题】力扣105从前序与中序遍历序列构造二叉树

题目来源

力扣105从前序与中序遍历序列构造二叉树

题目概述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

思路分析

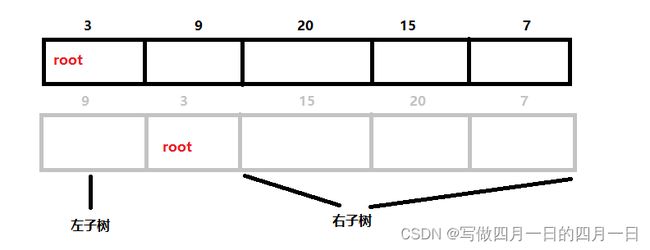
前序遍历的顺序是：根节点->左子树->右子树 中序遍历的顺序是：左子树->根节点->右子树 所以我们可以使用前序遍历确定树及其子树的根节点，利用中序遍历与之前确定下来的根节点来确定左右子树的范围。 使用力扣提供的例子

我们可以先找到根节点为3

然后就可以确定根节点的两个孩子节点，及其子树。

代码实现

java实现

public class Solution {

    Map inorderDataAndIndex;
    public TreeNode buildTree(int[] preorder, int[] inorder) {

        // 建立中序遍历数据与下标的映射
        inorderDataAndIndex = new HashMap(){{
            for (int i = 0; i < inorder.length; i++) {
                put(inorder[i],i);
            }
        }};

        return create(preorder,inorder, 0, preorder.length - 1, 0, inorder.length - 1);
    }

    TreeNode create(int[] preorder, int[] inorder, int pStart, int pEnd, int iStart, int iEnd) {
        if (pStart > pEnd) {
            return null;
        }
        // 前序遍历第一个节点为根节点
        TreeNode root = new TreeNode(preorder[pStart]);

        // 找到在中序遍历的位置
        int inorderIndex = inorderDataAndIndex.get(preorder[pStart]);

        // 左子树大小
        int leftSubTreeSize = inorderIndex - iStart;

        // 构建子树
        root.left = create(preorder,inorder, pStart + 1, pStart + leftSubTreeSize  , iStart, inorderIndex - 1);
        root.right = create(preorder,inorder, pStart + leftSubTreeSize + 1, pEnd  , inorderIndex + 1, iEnd);

        return root;
    }

}

c++实现

class Solution {
public:
    unordered_map inorder_data_and_index;
    TreeNode* buildTree(vector& preorder, vector& inorder) {
        // 建立中序遍历序列值与下标的映射，方便查找
        for (int i = 0; i < inorder.size(); i++) {
            inorder_data_and_index[inorder[i]] = i;
        }
        return create(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
    }

    TreeNode* create(vector& preorder, vector& inorder, int p_start, int p_end, int i_start, int i_end) {
        if (p_start > p_end) {
            return nullptr;
        }
        // 前序遍历第一个节点为根节点
        TreeNode* root = new TreeNode(preorder[p_start]);

        // 找到在中序遍历的位置
        int inorder_index = inorder_data_and_index[preorder[p_start]];

        // 左子树大小
        int left_sub_tree_size = inorder_index - i_start;

        // 构建子树
        root->left = create(preorder, inorder, p_start + 1, p_start + left_sub_tree_size, i_start, inorder_index - 1);
        root->right = create(preorder, inorder, p_start + left_sub_tree_size + 1, p_end, inorder_index + 1, i_end);

        return root;
    }
}