算法学习|Day17-二叉树|Leetcode110.平衡二叉树,Leetcode257. 二叉树的所有路径,Leetcode404.左叶子之和
目录
- 一、Leetcode110.平衡二叉树
-
- 题目描述
- 解题思路
- 方法:递归
- 总结
- 二、Leetcode257. 二叉树的所有路径
-
- 题目描述
- 解题思路
- 方法:递归
- 总结
- 三、Leetcode404.左叶子之和
-
- 题目描述
- 解题思路
- 方法一:递归
- 方法二:层序遍历
- 总结
一、Leetcode110.平衡二叉树
题目描述
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
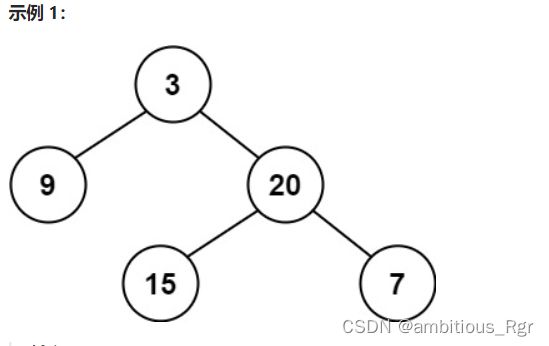
输入:root = [3,9,20,null,null,15,7]
输出:true
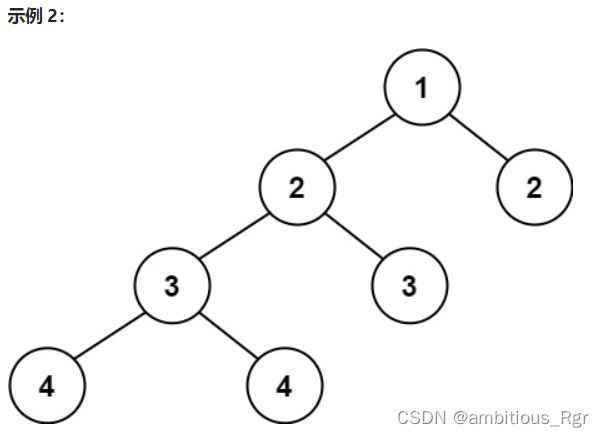
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
输入:root = []
输出:true
题目链接:力扣题目链接
解题思路
- 既要传递层数,也要传递子树是否平衡的信息(因为子树不平衡这棵树就不平衡)
方法:递归
-
确定递归的参数和返回值
参数是当前节点,返回值是根节点的高度 -
确定终止条件
遇到空节点了终止,返回0
if not root:
return 0
- 确定单层递归逻辑:
确定左右子树层数的差值,如果大于1,返回-1,反之返回计算后根节点高度
所以前面还要加入判断(先判断左右子树是否有传递上来的-1,如果有,直接返回-1)
numleft = self.gethigh(root.left)
numright = self.gethigh(root.right)
# 想清楚返回值,单层递归逻辑,如何保存左右子树层数和是否平衡的信息(-1)!
# 只要子树不平衡整棵树就不平衡,所以将-1传递上去!
if numleft == -1 or numright == -1 or abs(numleft - numright) > 1:
return -1
else:
return 1 + max(numleft, numright)
总代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if self.gethigh(root) != -1:
return True
else:
return False
def gethigh(self, root):
if not root:
return 0
numleft = self.gethigh(root.left)
numright = self.gethigh(root.right)
# 想清楚返回值,单层递归逻辑,如何保存左右子树层数和是否平衡的信息(-1)!
# 只要子树不平衡整棵树就不平衡,所以将-1传递上去!
if numleft == -1 or numright == -1 or abs(numleft - numright) > 1:
return -1
else:
return 1 + max(numleft, numright)
总结
- 用-1记录了左右子树不平衡的信息,很巧妙!
- 而且只要有-1就会一直传递到根节点,满足子树不平衡树就不平衡的原理。
二、Leetcode257. 二叉树的所有路径
题目描述
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
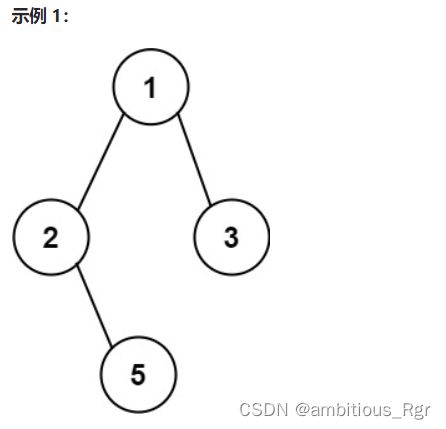
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
输入:root = [1]
输出:["1"]
题目链接:力扣题目链接
解题思路
- 选择前序遍历保留根节点到叶子节点的路径
- 使用回溯,记录到所有路径(叶子节点记录完就回退到上一个根节点)
方法:递归
-
确定递归的参数和返回值
参数是当前节点,返回值是当前路径path,最后结果result -
确定终止条件
找到叶子节点
if not cur.left and not cur.right
- 确定单层递归逻辑:
使用前序遍历
找到叶子节点后,用->连接当前记录的路径path,将完整的一条path加入result后,将叶子节点回溯(保留了叶子节点前的路径,继续遍历!)
path.append(cur.val)
if not cur.left and not cur.right:
paths = '->'.join(map(str, path))
result.append(paths)
return
if cur.left:
self.traversal(cur.left, path, result)
path.pop() # 回溯
if cur.right:
self.traversal(cur.right, path, result)
path.pop() # 回溯
总代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
path = []
result = []
if not root:
return []
self.traversal(root, path, result)
return result
def traversal(self, cur, path, result):
path.append(cur.val)
if not cur.left and not cur.right:
paths = '->'.join(map(str, path))
result.append(paths)
return
if cur.left:
self.traversal(cur.left, path, result)
path.pop() # 回溯
if cur.right:
self.traversal(cur.right, path, result)
path.pop() # 回溯
总结
- 初次使用回溯的思想,希望后面回溯算法好好理解
- 用path记录当前路径,遇到叶子节点保存路径,然后pop掉叶子节点继续遍历,非常巧妙!
三、Leetcode404.左叶子之和
题目描述
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
输入: root = [1]
输出: 0
题目链接:力扣题目链接
解题思路
- 重点是如何找到左叶子
- 终止条件先找到叶子,再判断是不是左叶子
方法一:递归
-
确定递归的参数和返回值
参数是当前节点,返回值是左叶子之和 -
确定终止条件
找到叶子节点
if not root.left and not root.right:
return 0
- 确定单层递归逻辑:
使用后序遍历
遇到左叶子的时候累加,最终返回和
numleft = self.sumOfLeftLeaves(root.left)
# 重点是如何找到左叶子!!
if root.left and not root.left.left and not root.left.right:
numleft = root.left.val
numright = self.sumOfLeftLeaves(root.right)
total = numleft + numright
总代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
if not root.left and not root.right:
return 0
numleft = self.sumOfLeftLeaves(root.left)
# 重点是如何找到左叶子!!
if root.left and not root.left.left and not root.left.right:
numleft = root.left.val
numright = self.sumOfLeftLeaves(root.right)
total = numleft + numright
return total
方法二:层序遍历
- 遍历到每一层,判断cur.left的时候,继续判断是不是左叶子!
- 继续判断左叶子: cur.left.left和cur.left.right为空!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
que = collections.deque([root])
total = 0
while que:
size = len(que)
for _ in range(size):
cur = que.popleft()
if cur.left:
que.append(cur.left)
# 判断是否是左叶子!!!
if not cur.left.left and not cur.left.right:
total += cur.left.val
if cur.right:
que.append(cur.right)
return total
总结
- 左叶子的条件是,cur.left.left == None 和 cur.left.right == None
- 单层递归的思路要想清楚!!
- 层序遍历也可以做,加上对左叶子的判断!
心得:到Day17啦,二叉树这块的递归开始变难了,首先是终止条件不好确定,其次是单层递归的逻辑不好想,多回顾一下今天的题目吧…