【小呆的力学笔记】弹塑性力学的初步认知五:初始屈服条件(1)
文章目录
-
-
- 3. 初始屈服条件
-
- 3.1 两个假设以及屈服条件基本形式
- 3.2 π \pi π平面、Lode参数
- 3.3 屈服曲线的一般特征
-
3. 初始屈服条件
3.1 两个假设以及屈服条件基本形式
在简单拉伸时,材料的屈服很明确,即
σ > σ s (1) \sigma\gt\sigma_s\tag{1} σ>σs(1)
那么当一般应力状态下,材料的屈服条件是怎样的形式呢?参考简单拉伸,我们可以写下通用形式的屈服条件
f ( σ i j ) ≥ 0 , 屈服 f ( σ i j ) < 0 , 弹性 (2) f(\sigma_{ij}) \ge0 \quad, \quad屈服\\ f(\sigma_{ij})\lt 0 \quad, \quad弹性\tag{2} f(σij)≥0,屈服f(σij)<0,弹性(2)
即当 f ( σ i j ) = 0 f(\sigma_{ij}) =0 f(σij)=0时就是屈服时刻。
我们在讨论一般的金属材料的塑性时,为了简化讨论,先提出两个假设:
1。 材料在初始屈服前,是各项同性的。
2。 静水应力不影响材料的塑性。
因此,屈服只与应力偏量有关,那么式(2)就能转化成如下的形式
f ( J 1 , J 2 , J 3 ) = 0 (3) f(J_1,J_2,J_3)=0\tag{3} f(J1,J2,J3)=0(3)
进一步,有 J 1 = 0 J_1=0 J1=0,那么
f ( J 2 , J 3 ) = 0 (4) f(J_2,J_3)=0\tag{4} f(J2,J3)=0(4)
3.2 π \pi π平面、Lode参数
在主应力空间中,一点的应力状态 ( σ 1 , σ 2 , σ 3 ) (\sigma_1,\sigma_2,\sigma_3) (σ1,σ2,σ3)为P点坐标,那么
O P → = σ 1 i 1 → + σ 2 i 2 → + σ 3 i 3 → (5) \overrightarrow{OP}=\sigma_1\overrightarrow{i_1}+\sigma_2\overrightarrow{i_2}+\sigma_3\overrightarrow{i_3}\tag{5} OP=σ1i1+σ2i2+σ3i3(5)
将上式分解
O P → = σ 1 i 1 → + σ 2 i 2 → + σ 3 i 3 → = σ m i 1 → + σ m i 2 → + σ m i 3 → + s 1 i 1 → + s 2 i 2 → + s 3 i 3 → = O N → + O Q → (6) \begin{aligned} \overrightarrow{OP}&=\sigma_1\overrightarrow{i_1}+\sigma_2\overrightarrow{i_2}+\sigma_3\overrightarrow{i_3}\\ &=\sigma_m\overrightarrow{i_1}+\sigma_m\overrightarrow{i_2}+\sigma_m\overrightarrow{i_3}+s_1\overrightarrow{i_1}+s_2\overrightarrow{i_2}+s_3\overrightarrow{i_3}\\ &=\overrightarrow{ON}+\overrightarrow{OQ} \end{aligned}\tag{6} OP=σ1i1+σ2i2+σ3i3=σmi1+σmi2+σmi3+s1i1+s2i2+s3i3=ON+OQ(6)
上式中, O N → \overrightarrow{ON} ON、 O Q → \overrightarrow{OQ} OQ如下图1所示。
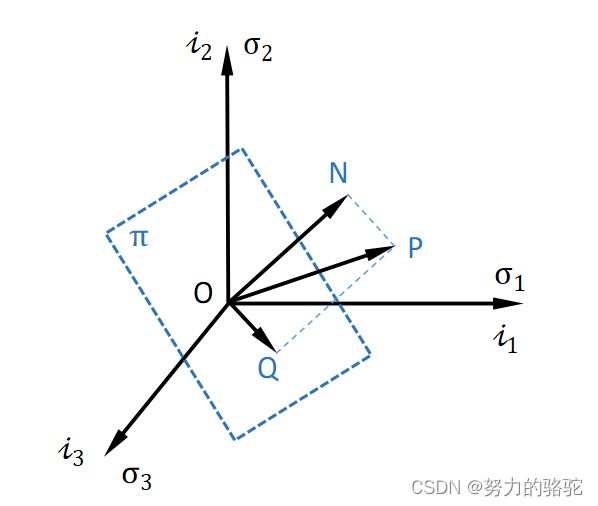
图 1 应力分解图 图1\quad 应力分解图 图1应力分解图
且
O N → ⋅ O Q → = ( σ m , σ m , σ m ) ⋅ ( s 1 , s 2 , s 3 ) = σ m ⋅ ( s 1 + s 2 + s 3 ) = 0 (7) \overrightarrow{ON}\cdot\overrightarrow{OQ}=(\sigma_m,\sigma_m,\sigma_m)\cdot (s_1,s_2,s_3)=\sigma_m\cdot(s_1+s_2+s_3)=0\tag{7} ON⋅OQ=(σm,σm,σm)⋅(s1,s2,s3)=σm⋅(s1+s2+s3)=0(7)
因此 O N → \overrightarrow{ON} ON、 O Q → \overrightarrow{OQ} OQ互相垂直,其中 O N → \overrightarrow{ON} ON的单位向量为 ( 1 3 , 1 3 , 1 3 ) (\frac{1}{\sqrt 3},\frac{1}{\sqrt 3},\frac{1}{\sqrt 3}) (31,31,31),以此为法向量,并过原点O的平面方程为
σ 1 + σ 2 + σ 3 = 0 (8) \sigma_1+\sigma_2+\sigma_3=0\tag{8} σ1+σ2+σ3=0(8)
不难发现,任意的应力状态点 ( σ 1 , σ 2 , σ 3 ) (\sigma_1,\sigma_2,\sigma_3) (σ1,σ2,σ3)在这个平面上的投影点Q在主应力坐标系中的坐标为 ( s 1 , s 2 , s 3 ) (s_1,s_2,s_3) (s1,s2,s3),这代表该应力状态的静水应力部分经过投影变为零。由3.1的第二个假设,静水应力不影响材料的塑性行为,因此只需要在此平面上讨论屈服条件即可,我们把这个平面称为 π \pi π平面。
材料屈服条件形式如式(3),因此在 π \pi π平面内讨论式(3)的形式。为了方便讨论,需在 π \pi π平面内建立相应的坐标系。
将主应力空间的基向量 ( i 1 → , i 2 → , i 3 → ) (\overrightarrow{i_1},\overrightarrow{i_2},\overrightarrow{i_3}) (i1,i2,i3)在 π \pi π平面上的投影记为 ( i 1 ′ → , i 2 ′ → , i 3 ′ → ) (\overrightarrow{i_1^{'}},\overrightarrow{i_2^{'}},\overrightarrow{i_3^{'}}) (i1′,i2′,i3′),讨论 i i → \overrightarrow{i_i} ii和 i i ′ → \overrightarrow{i_i^{'}} ii′的关系。以 i 1 → \overrightarrow{i_1} i1为例, i 1 ′ → \overrightarrow{i_1^{'}} i1′为其在 π \pi π平面上的投影,如图2, π \pi π平面法向量 O N → \overrightarrow{ON} ON与 i 1 → \overrightarrow{i_1} i1夹角为 α \alpha α, i 1 → \overrightarrow{i_1} i1和 i 1 ′ → \overrightarrow{i_1^{'}} i1′夹角为 β \beta β,并且 α + β = 9 0 。 \alpha+\beta=90^。 α+β=90。,由 cos α = 1 3 \cos\alpha=\frac{1}{\sqrt 3} cosα=31可知, cos β = 2 3 \cos\beta=\sqrt\frac{2}{ 3} cosβ=32。那么有 ∣ i 1 ′ → ∣ = 2 3 |\overrightarrow{i_1^{'}}|=\sqrt\frac{2}{ 3} ∣i1′∣=32, i 2 ′ → 、 i 3 ′ → \overrightarrow{i_2^{'}}、\overrightarrow{i_3^{'}} i2′、i3′也同理可得,并且不难得出 i 1 ′ → \overrightarrow{i_1^{'}} i1′、 i 2 ′ → \overrightarrow{i_2^{'}} i2′、 i 3 ′ → \overrightarrow{i_3^{'}} i3′在 π \pi π平面上夹角为 12 0 。 120^。 120。。
图 2 基向量投影 图2\quad 基向量投影 图2基向量投影
i 1 ′ → \overrightarrow{i_1^{'}} i1′、 i 2 ′ → \overrightarrow{i_2^{'}} i2′、 i 3 ′ → \overrightarrow{i_3^{'}} i3′在 π \pi π平面上的投影如图3,其中 i i ′ → \overrightarrow{i_i^{'}} ii′的模为 cos β \cos\beta cosβ。以 i 2 ′ → \overrightarrow{i_2^{'}} i2′为 y y y轴,右手定则确定 x x x轴。 O Q → \overrightarrow{OQ} OQ在主应力空间中分量为 s 1 i 1 → s_1\overrightarrow{i_1} s1i1、 s 2 i 2 → s_2\overrightarrow{i_2} s2i2、 s 3 i 3 → s_3\overrightarrow{i_3} s3i3,那么投影到 π \pi π平面上,就是 s 1 i 1 ′ → s_1\overrightarrow{i_1^{'}} s1i1′、 s 2 i 2 ′ → s_2\overrightarrow{i_2^{'}} s2i2′、 s 3 i 3 ′ → s_3\overrightarrow{i_3^{'}} s3i3′,那么在 x − y x-y x−y坐标系中,将 s 1 i 1 ′ → s_1\overrightarrow{i_1^{'}} s1i1′、 s 2 i 2 ′ → s_2\overrightarrow{i_2^{'}} s2i2′、 s 3 i 3 ′ → s_3\overrightarrow{i_3^{'}} s3i3′写成 ( x , y ) (x,y) (x,y)分量的形式,如下所示。
s 1 i 1 ′ → = ( s 1 cos 3 0 。 , − s 1 cos 6 0 。 ) ⋅ cos β s 2 i 2 ′ → = ( 0 , s 2 ) ⋅ cos β s 1 i 1 ′ → = ( − s 3 cos 6 0 。 , − s 3 cos 3 0 。 ) ⋅ cos β (9) s_1\overrightarrow{i_1^{'}}=(s_1\cos30^。,-s_1\cos60^。)\cdot\cos\beta\\ s_2\overrightarrow{i_2^{'}}=(0,s_2)\cdot\cos\beta\\ s_1\overrightarrow{i_1^{'}}=(-s_3\cos60^。,-s_3\cos30^。)\cdot\cos\beta\tag{9} s1i1′=(s1cos30。,−s1cos60。)⋅cosβs2i2′=(0,s2)⋅cosβs1i1′=(−s3cos60。,−s3cos30。)⋅cosβ(9)
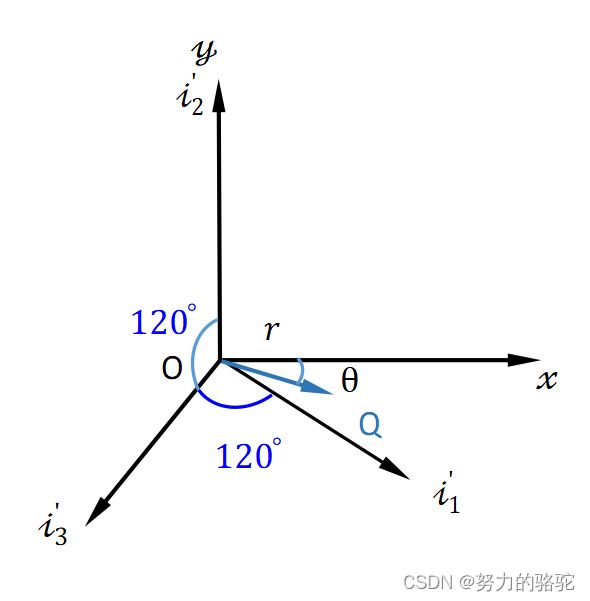
图 3 π 平面中基向量投影 图3\quad \pi平面中基向量投影 图3π平面中基向量投影
因此, O Q → \overrightarrow{OQ} OQ在 π \pi π平面上的坐标为
x = ( s 1 cos 3 0 。 + 0 − s 3 cos 6 0 。 ) cos β = 2 2 ( s 1 − s 3 ) = 2 2 ( σ 1 − σ 3 ) y = ( − s 1 cos 6 0 。 + s 2 − s 3 cos 3 0 。 ) cos β = 1 6 ( 2 s 2 − s 1 − s 3 ) = 1 6 ( 2 σ 2 − σ 1 − σ 3 ) (10) \begin{aligned} &x=(s_1\cos30^。+0-s_3\cos60^。)\cos\beta=\frac{\sqrt2}{2}(s_1-s_3)=\frac{\sqrt2}{2}(\sigma_1-\sigma_3)\\ &y=(-s_1\cos60^。+s_2-s_3\cos30^。)\cos\beta=\frac{1}{\sqrt6}(2s_2-s_1-s_3)=\frac{1}{\sqrt6}(2\sigma_2-\sigma_1-\sigma_3)\end{aligned}\tag{10} x=(s1cos30。+0−s3cos60。)cosβ=22(s1−s3)=22(σ1−σ3)y=(−s1cos60。+s2−s3cos30。)cosβ=61(2s2−s1−s3)=61(2σ2−σ1−σ3)(10)
如果用极坐标的形式表示,则有
r = x 2 + y 2 = 1 2 ( σ 1 − σ 3 ) 2 + 1 6 ( 2 σ 2 − σ 1 − σ 3 ) 2 tan θ = y x = 1 6 ( 2 σ 2 − σ 1 − σ 3 ) 2 2 ( σ 1 − σ 3 ) = 1 3 ⋅ 2 σ 2 − σ 1 − σ 3 σ 1 − σ 3 = 1 3 ⋅ μ σ (11) \begin{aligned} &r=\sqrt{x^2+y^2}=\sqrt{\frac{1}{2}(\sigma_1-\sigma_3)^2+\frac{1}{6}(2\sigma_2-\sigma_1-\sigma_3)^2}\\ &\tan\theta=\frac{y}{x}=\frac{ \frac{1}{\sqrt6}(2\sigma_2-\sigma_1-\sigma_3) }{ \frac{\sqrt2}{2}(\sigma_1-\sigma_3) }=\frac{1}{\sqrt3}\cdot\frac{2\sigma_2-\sigma_1-\sigma_3}{\sigma_1-\sigma_3}=\frac{1}{\sqrt3}\cdot\mu_\sigma \end{aligned}\tag{11} r=x2+y2=21(σ1−σ3)2+61(2σ2−σ1−σ3)2tanθ=xy=22(σ1−σ3)61(2σ2−σ1−σ3)=31⋅σ1−σ32σ2−σ1−σ3=31⋅μσ(11)
其中 μ σ = 2 σ 2 − σ 1 − σ 3 σ 1 − σ 3 \mu_\sigma=\frac{2\sigma_2-\sigma_1-\sigma_3}{\sigma_1-\sigma_3} μσ=σ1−σ32σ2−σ1−σ3称为Lode参数,它表示了主应力之间的相对比值。
3.3 屈服曲线的一般特征
现在可以讨论屈服条件,在主应力空间中屈服条件 f ( σ i j ) = f ( J 2 , J 3 ) = 0 f(\sigma_{ij})=f(J_2,J_3)=0 f(σij)=f(J2,J3)=0形成一个以 O N → \overrightarrow{ON} ON为母线的柱面(静水压力不影响塑性)。柱面和 π \pi π平面形成的截面线称为屈服曲线。
根据3.1的第一个假设:材料在初始屈服前,是各项同性的,那么屈服曲线肯定式关于三个坐标轴对称的,三个坐标轴正方向在 π \pi π平面上是夹角是一样的为 12 0 。 120^。 120。,三个坐标轴负方向在 π \pi π平面上是夹角是一样为 12 0 。 120^。 120。,那么一个坐标轴的负方向和其他两个坐标轴的正方向夹 6 0 。 60^。 60。,如图4。
屈服曲线关于坐标轴正方向对称,那么屈服曲线对称角度为 12 0 。 120^。 120。,同时屈服曲线关于坐标轴负方向对称,那么屈服曲线对称角度为 6 0 。 60^。 60。。即在图中 A C ′ ⌢ \overset{\LARGE{\frown}}{AC'} AC′⌢、 A B ′ ⌢ \overset{\LARGE{\frown}}{AB'} AB′⌢对称,同时 A C ′ ⌢ \overset{\LARGE{\frown}}{AC'} AC′⌢、 B C ′ ⌢ \overset{\LARGE{\frown}}{BC'} BC′⌢对称,因此只需要知道 6 0 。 60^。 60。的曲线,就能完整确定整条曲线。
同时,在各项同性的同时,假设压缩和拉伸性能相等,则 A C ′ ⌢ \overset{\LARGE{\frown}}{AC'} AC′⌢自己是关于bb’对称的,那么只需要知道 3 0 。 30^。 30。的曲线就能完整确定整条曲线。

图 4 π 平面中坐标轴投影 图4\quad \pi平面中坐标轴投影 图4π平面中坐标轴投影
