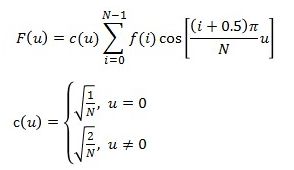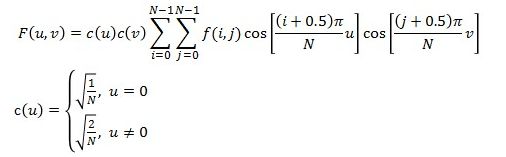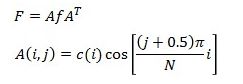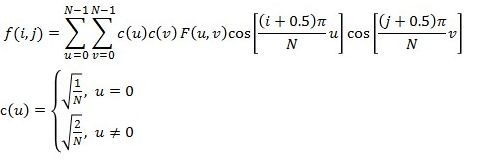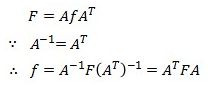【DCT笔记】DCT变换、DCT反变换、分块DCT变换
DCT变换、DCT反变换、分块DCT变换
欢迎转载,但请注明出处!
一、引言
DCT变换的全称是离散余弦变换(Discrete Cosine Transform),主要用于将数据或图像的压缩,能够将空域的信号转换到频域上,具有良好的去相关性的性能。DCT变换本身是无损的,但是在图像编码等领域给接下来的量化、哈弗曼编码等创造了很好的条件,同时,由于DCT变换时对称的,所以,我们可以在量化编码后利用DCT反变换,在接收端恢复原始的图像信息。DCT变换在当前的图像分析已经压缩领域有着极为广大的用途,我们常见的JPEG静态图像编码以及MJPEG、MPEG动态编码等标准中都使用了DCT变换。
二、一维DCT变换
一维DCT变换时二维DCT变换的基础,所以我们先来讨论下一维DCT变换。一维DCT变换共有8种形式,其中最常用的是第二种形式,由于其运算简单、适用范围广。我们在这里只讨论这种形式,其表达式如下:
其中,f(i)为原始的信号,F(u)是DCT变换后的系数,N为原始信号的点数,c(u)可以认为是一个补偿系数,可以使DCT变换矩阵为正交矩阵。
三、二维DCT变换
二维DCT变换其实是在一维DCT变换的基础上在做了一次DCT变换,其公式如下:
由公式我们可以看出,上面只讨论了二维图像数据为方阵的情况,在实际应用中,如果不是方阵的数据一般都是补齐之后再做变换的,重构之后可以去掉补齐的部分,得到原始的图像信息,这个尝试一下,应该比较容易理解。
另外,由于DCT变换高度的对称性,在使用Matlab进行相关的运算时,我们可以使用更简单的矩阵处理方式:
接下来利用Matlab对这个过程进行仿真处理:
1 clear; 2 clc; 3 X=round(rand(4)*100) %产生随机矩阵 4 A=zeros(4); 5 for i=0:3
6 for j=0:3
7 if i==0
8 a=sqrt(1/4); 9 else
10 a=sqrt(2/4); 11 end 12 A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4); 13 end 14 end 15 Y=A*X*A' %DCT变换 16 YY=dct2(X) %Matlab自带的dct变换
运行结果为:
1 X =
2
3 42 66 68 66
4 92 4 76 17
5 79 85 74 71
6 96 93 39 3
7
8
9 Y =
10
11 242.7500 48.4317 -9.7500 23.5052
12 -12.6428 -54.0659 7.4278 22.7950
13 -6.2500 10.7158 -19.7500 -38.8046
14 40.6852 -38.7050 -11.4653 -45.9341
15
16
17 YY =
18
19 242.7500 48.4317 -9.7500 23.5052
20 -12.6428 -54.0659 7.4278 22.7950
21 -6.2500 10.7158 -19.7500 -38.8046
22 40.6852 -38.7050 -11.4653 -45.9341
由上面的结果我们可以看出,我们采用的公式的方法和Matlab自带的dct变化方法结果是一致的,所以验证了我们方法的正确性。
如果原始信号是图像等相关性较大的数据的时候,我们可以发现在变换之后,系数较大的集中在左上角,而右下角的几乎都是0,其中左上角的是低频分量,右下角的是高频分量,低频系数体现的是图像中目标的轮廓和灰度分布特性,高频系数体现的是目标形状的细节信息。DCT变换之后,能量主要集中在低频分量处,这也是DCT变换去相关性的一个体现。
之后在量化和编码阶段,我们可以采用“Z”字形编码,这样就可以得到大量的连续的0,这大大简化了编码的过程。
四、二维DCT反变换
在图像的接收端,根据DCT变化的可逆性,我们可以通过DCT反变换恢复出原始的图像信息,其公式如下:
同样的道理,我们利用之前的矩阵运算公司可以推导出DCT反变换相应的矩阵形式:
下面我们用Matlab对这个过程进行仿真:
1 clear; 2 clc; 3 X=[ 4 61 19 50 20
5 82 26 61 45
6 89 90 82 43
7 93 59 53 97] %原始的数据 8 A=zeros(4); 9 for i=0:3
10 for j=0:3
11 if i==0
12 a=sqrt(1/4); 13 else
14 a=sqrt(2/4); 15 end 16 A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4); %生成变换矩阵 17 end 18 end 19 Y=A*X*A' %DCT变换后的矩阵 20 X1=A'*Y*A %DCT反变换恢复的矩阵
运行结果为:
1 X =
2
3 61 19 50 20
4 82 26 61 45
5 89 90 82 43
6 93 59 53 97
7
8
9 Y =
10
11 242.5000 32.1613 22.5000 33.2212
12 -61.8263 7.9246 -10.7344 30.6881
13 -16.5000 -14.7549 22.5000 -6.8770
14 8.8322 16.6881 -35.0610 -6.9246
15
16
17 X1 =
18
19 61.0000 19.0000 50.0000 20.0000
20 82.0000 26.0000 61.0000 45.0000
21 89.0000 90.0000 82.0000 43.0000
22 93.0000 59.0000 53.0000 97.0000
我们可以看到反变换后无损的恢复了原始信息,所以证明了方法的正确性。但是在实际过程中,需要量化编码或者直接舍弃高频分量等处理,所以会出现一定程度的误差,这个是不可避免的。
五、分块DCT变换
在实际的图像处理中,DCT变换的复杂度其实是比较高的,所以通常的做法是,将图像进行分块,然后在每一块中对图像进行DCT变换和反变换,在合并分块,从而提升变换的效率。具体的分块过程中,随着子块的变大,算法复杂度急速上升,但是采用较大的分块会明显减少图像分块效应,所以,这里面需要做一个折中,在通常使用时,大都采用的是8*8的分块。
Matlab的 blkproc 函数可以帮我们很方便的进行分块处理,下面给出我们的处理过程:
1 clear; 2 clc; 3
4 X=imread('pepper.bmp'); 5 X=double(X); 6 [a,b]=size(X); 7 Y=blkproc(X,[8 8],'dct2'); 8 X1=blkproc(Y,[8 8],'idct2'); 9
10 figure 11 subplot(1,3,1); 12 imshow(uint8(X)); 13 title('原始图'); 14
15 subplot(1,3,2); 16 imshow(uint8(Y)); 17 title('分块DCT变换图'); 18
19 subplot(1,3,3); 20 imshow(uint8(X1)); 21 title('分块DCT恢复图'); 22
23 Y1=dct2(X); 24 X10=idct2(Y1); 25
26 figure 27 subplot(1,3,1); 28 imshow(uint8(X)); 29 title('原始图'); 30
31 subplot(1,3,2); 32 imshow(uint8(Y1)); 33 title('DCT变换图'); 34
35 subplot(1,3,3); 36 imshow(uint8(X10)); 37 title('DCT反变换恢复图');
运行结果为:
从图中,我们可以明显看出DCT变换与分块DCT变换在使用时的区别。
六、小结
DCT、DWT等是图像处理的基础知识,之前一直有用到,但是没怎么好好整理下,今天在做稀疏编码的时候正好有用到,就顺便整了下,希望能够给后来者一些提示。
我的新浪微博:http://weibo.com/3109428257/profile?rightmod=1&wvr=5&mod=personinfo
Reference:http://wuyuans.com/2012/11/dct2/