Catalan数

什么是Catalan数

说到Catalan数，就不得不提及Catalan序列，Catalan序列是一个整数序列，其通项公式是我们从中取出的就叫做第n个Catalan数，前几个Catalan数是：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, …咋看之下没什么特别的，但是Catalan数却是许多计数问题的最终形式。

Catalan数的一些性质

Catalan数的基本公式就是上个部分所列出的那样，但是却有一些变形和具体的性质：

1、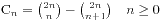

这是根据原来的式子推导出来的，大概过程是这样的：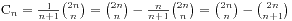

2、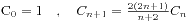

这个递推式很容易可以从原来的式子中获得

3、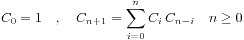

4、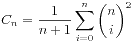

5、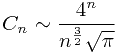

这个是Catalan数的增长趋势。

Catalan数在组合计算中的应用

在《组合数学》（机械工业出版社）一书中，介绍Catalan数是由其一个应用推导出的公式，其具体的描述如下：

n个+1和n个-1构成2n项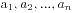，其部分和满足的序列个数等于第n个Catalan数。

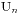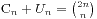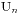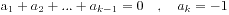其证明也不难，我们假设不满足条件的序列个数为，那么就有。剩下的工作就是求了，我们假设有一个最小的k令。由于这里k是最小的，所以必有，并且k是一个奇数。此时我们将前k项中的+1变为-1，将-1变为+1,那么就得到一个有(n+1)个+1和(n-1)个-1的序列了，这样的序列个数就是我们要求的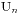，数值大小为 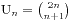。那么我们就得到了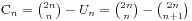，就是我们前面的公式。

在具体的组合数问题中，很多都可以转换为Catalan数进行最后的计算，如下：

1、如上文所说，对于任意的k，前k个元素中-1的个数小等于+1的个数的序列计数，我们可以不停地变换形式，比如将-1看成右括号，+1看成左括号，就变成了合法括号表达式的个数。比如2个左括号和2个右括号组成的合法表达式有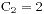种，是()()和(())。

2、既然如上一点都把括号加上去了，那么顺便就再次转换，n+1个数连乘，乘法顺序有种，比如我们三个数连乘a*b*c，那么等于在式子上加括号，有2种乘法顺序，分别是(ab)c和a(bc)。貌似对应关系比较模糊，我们取n为3来看看，n为3的时候就是4个数相乘了，那么我们设为abcd，最初的标号定在a上，我们对于n为3得到合法的括号序列有5个，分别是：((()))，()(())，()()()，(())()和(()())，那么我们将一个左括号看成是当前操作数指针往右移动一个位置，一个右括号看成是当前操作数和左边最近的一块操作数相乘起来，那么对应的五个表达式就是：a(b(cd))，(ab)(cd)，((ab)c)d，(a(bc))d和a((bc)d)，他们之间是一一对应关系。

3、n个节点的二叉树的所有可能形态数为，这一点很容易证明，我们考虑随便取一个节点作为根，那么他左边和右边的儿子节点个数就确定了，假定根节点标号为x，那么左子树的标号就从1到x-1,共x-1个，右子树的标号就从x+1到n，共n-x个，那么我们的x从1取到n，就获得了所有的情况数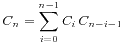。这个式子就是我们性质3的式子。

4、n个非叶节点的满二叉树的形态数（对称后得到的二叉树除非自己本身对称，否则算是不同），这里取Wikipedia上的一张图片说明问题：

这里要求满二叉树，实际上就是在上一点的每个子节点的空儿子上都加上叶子，就形成了我们的图了，那么我们要求的结果就是Catalan数。

5、对于一个n*n的正方形网格，每次我们能向右或者向上移动一格，那么从左下角到右上角的所有在副对角线右下方的路径总数为。同样引用Wikipedia上的一张图片来表示：

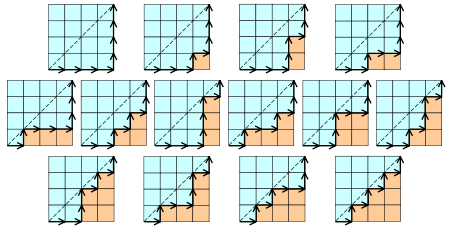
我们将一条水平边记为+1,垂直边记为-1,那么就组成了一个n个+1和n个-1的序列，我们所要保证的就是前k步中水平边的个数不小于垂直边的个数，换句话说前k个元素的和非负，就是我们关于Catalan数的定义。

6、凸n+2边形进行三角形分割（只连接顶点对形成n个三角形）数：

7、n个数入栈后的出栈的排列总数是。例如1,2,3入栈的出栈排序有123，132，213，231和321五种

　　一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?

　　分析

　　对于每一个数来说，必须进栈一次、出栈一次。我们把进栈设为状态‘1’，出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b)，因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数，1的累计数不小于0的累计数的方案种数。

　　在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求（由左而右扫描，0的累计数大于1的累计数）的方案数即为所求。

　　不符合要求的数的特征是由左而右扫描时，必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数，此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换，使之成为n-m个0和n-m-1个1，结果得1个由n+1个0和n-1个1组成的2n位数，即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。

　　反过来，任何一个由n+1个0和n-1个1组成的2n位二进制数，由于0的个数多2个，2n为偶数，故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换，使之成为由n个0和n个1组成的2n位数，即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。

　　因而不合要求的2n位数与n＋1个0，n－1个1组成的排列一一对应。

　　显然，不符合要求的方案数为c(2n,n+1)。由此得出 输出序列的总数目=c(2n,n)-c(2n,n+1)=1/(n+1)*c(2n,n)。

8、对于集合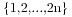的不交叉划分的数目为，这里解释一下不交叉划分，我们对于集合{a,b}和{c,d}，假设他们组成了两个区间[a,b]和[c,d]，我们假设两个区间不重合，那么以下四种情况当做是不交叉的：a<c<d<b，a<b<c<d，c<a<b<d与c<d<a<b，就是说两个区间可以包含或者相离，那么此时我们称集合{a,b}和{c,d}是不交叉的。对于集合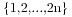，将里面元素两两分为一子集，共n个，若任意两个子集都是不交叉的，那么我们称此时的这个划分为一个不交叉划分。此时不交叉的划分数就是我们的了，证明也很容易，我们将每个子集中较小的数用左括号代替，较大的用右括号代替，那么带入原来的1至2n的序列中就形成了合法括号问题，就是我们第二点的结论。例如我们的集合{1,2,3,4,5,6}的不交叉划分有五个：{{1,2},{3,4},{5,6}}，{{1,2},{3,6},{4,5}}，{{1,4},{2,3},{5,6}}，{{1,6},{2,3},{4,5}}和{{1,6},{2,5},{3,4}}。

9、n层的阶梯切割为n个矩形的切法数也是。如下图所示：

 这个证明是怎么进行的呢？我们先绘制如下的一张图片，即n为5的时候的阶梯：

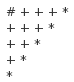
我们注意到每个切割出来的矩形都必需包括一块标示为*的小正方形，那么我们此时枚举每个*与#标示的两角作为矩形，剩下的两个小阶梯就是我们的两个更小的子问题了，于是我们的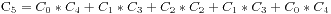注意到这里的式子就是我们前面的性质3,因此这就是我们所求的结果了。

10、在一个2*n的格子中填入1到2n这些数值使得每个格子内的数值都比其右边和上边的所有数值都小的情况数也是。

11、平面上连接可以形成凸包的2n个点分成2个一组连成n条线段，两两线段之间不相交的情况总数是，这里实际上和第7点本质上是一样的，这里就不解释了。

Catalan数问题的一个变形：

n+m个人排队买票，并且满足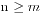，票价为50元，其中n个人各手持一张50元钞票，m个人各手持一张100元钞票，除此之外大家身上没有任何其他的钱币，并且初始时候售票窗口没有钱，问有多少种排队的情况数能够让大家都买到票。

这个题目是Catalan数的变形，不考虑人与人的差异，如果m=n的话那么就是我们初始的Catalan数问题，也就是将手持50元的人看成是+1，手持100元的人看成是-1，任前k个数值的和都非负的序列数。

这个题目区别就在于n>m的情况，此时我们仍然可以用原先的证明方法考虑，假设我们要的情况数是，无法让每个人都买到的情况数是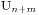，那么就有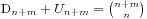，此时我们求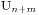，我们假设最早买不到票的人编号是k，他手持的是100元并且售票处没有钱，那么将前k个人的钱从50元变成100元，从100元变成50元，这时候就有n+1个人手持50元，m-1个手持100元的，所以就得到，于是我们的结果就因此得到了，表达式是。

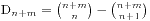关于Catalan数的变形还有很多，本身组合数学就是一门十分有趣的学科，通过不停地分析，求解我们能够不断增加自己思维的严谨性和全面性。

 

(注：该篇非原创，只是觉得较其他关于Catalan数的讲解较好而整理过来)

 

hdu 3398 String

给出n个1，m个0，组成一个串，要求这个串的任意前缀都有1的个数>=0的个数
    求满足这样的串的个数
    n,m <= 10^6

    脑残丫，很明显的“进栈出栈”，居然没反应
    计数公式为
        (n+m, m) - (n+m, m-1)

            (n+m)!(n-m+1)
    =    ------------------
           (n+1)!m!

#include<stdio.h>
#include<string.h>
#define nmax 2000001
#define nnum 20100501
#define LL long long
int plen, flag[nmax], prime[nmax];
int n, m;
void init() {
    memset(flag, -1, sizeof(flag));
    int i, j;
    for (i = 2, plen = 0; i < nmax; i++) {
        if (flag[i]) {
            prime[plen++] = i;
        }
        for (j = 0; j < plen && i * prime[j] < nmax; j++) {
            flag[i * prime[j]] = 0;
            if (i % prime[j] == 0) {
                break;
            }
        }
    }
}
int getNum(int a, int b) {
    int res;
    res = 0;
    while (a) {
        res += a / b;
        a /= b;
    }
    return res;
}
int modular_exp(int a, int b) {
    LL res, temp;
    res = 1, temp = a % nnum;
    while (b) {
        if (b & 1) {
            res = res * temp % nnum;
        }
        temp = temp * temp % nnum;
        b >>= 1;
    }
    return (int) res;
}
void solve() {
    int i, temp, te;
    LL res;
    te = n + 1 - m;
    for (i = 0, res = 1; (i < plen) && (prime[i] <= n + m); i++) {
        temp = 0;
        while (te % prime[i] == 0) {
            temp++;
            te /= prime[i];
        }
        temp += getNum(n + m, prime[i]) - getNum(m, prime[i])
                - getNum(n + 1, prime[i]);
        res = (res * modular_exp(prime[i], temp)) % nnum;
    }
    printf("%I64d\n", res);
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("in.data", "r", stdin);
#endif
    int T;
    init();
    while (scanf("%d", &T) != EOF) {
        while (T--) {
            scanf("%d %d", &n, &m);
            if (n < m) {
                puts("0");
                continue;
            }
            solve();
        }
    }
    return 0;
}

 

/*
 * hdu 1023 1130 1134 2067
 */
import java.math.BigInteger;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        BigInteger[] num = new BigInteger[101];
        BigInteger r, one, two;
        int i;
        one = BigInteger.ONE;
        two = BigInteger.valueOf(2);
        num[0] = BigInteger.ONE;
        for (i = 1; i < 101; i++) {
            r = BigInteger.valueOf(i);
            num[i] = num[i - 1].multiply(two).multiply(
                    two.multiply(r).subtract(one)).divide(r.add(one));
        }
        while (cin.hasNext()) {
            i = cin.nextInt();
            if (i == -1) {
                break;
            }
            System.out.println(num[i]);
        }
    }
}

 

/*
 * fzu1775.c
 *
 *  Created on: 2011-9-6
 *      Author: bjfuwangzhu
 */
/*
但是递推公式里面的系数含有除法，于是在对m取模的时候，想到求n+1的乘法逆元。
但是这里n+1和m不一定互素。于是我们可以将Fn看成两部分的乘积，一部分是与m互素的部分，
另一部分是不与m互素的部分。为了达到这个目的，我们可以先将m分解质因素，得到m中包含的所有不同的素因子，
然后在递推求解时，将4*i-2和i+1中与m互素的部分单独拿出来，形成a/b的形式，
再将与m不互素的素因子拿出来上下约分后得到各素因子的个数加到一个用于记录的数组中去，
形成Fi中与m不互素的部分。而对于a/b来说，可以乘上前一个卡特兰数与m互质的部分，
再乘上b的逆元得到当前卡特兰数与m互质的部分，更新记录变量值。
将此变量的值乘上数组中的各素因子然后取模便得到当前卡特兰数模m的值。求完每一个后，相加取模即可。
 */
#include<stdio.h>
#include<string.h>
#include<math.h>
#define LL long long
#define nmax 200001
int prime[nmax], flag[nmax], factor[nmax], cfactor[nmax];
int x, y, plen;
void init() {
    memset(flag, -1, sizeof(flag));
    int i, j;
    for (i = 2, plen = 0; i < nmax; i++) {
        if (flag[i]) {
            prime[plen++] = i;
        }
        for (j = 0; (j < plen) && (i * prime[j] < nmax); j++) {
            flag[i * prime[j]] = 0;
            if (i % prime[j] == 0) {
                break;
            }
        }
    }
}
int modular_exp(int a, int b, int c) {
    LL res, temp;
    temp = a % c, res = 1;
    while (b) {
        if (b & 1) {
            res = res * temp % c;
        }
        b >>= 1;
        temp = temp * temp % c;
    }
    return res;
}
void extend_gcd(int a, int b) {
    if (b == 0) {
        x = 1, y = 0;
        return;
    }
    extend_gcd(b, a % b);
    int tx = x;
    x = y;
    y = tx - a / b * y;
}
void solve(int n, int m) {
    int i, j, k, temp, mm;
    LL res, res0, res1;
    mm = m;
    temp = (int) (sqrt(m * 1.0));
    for (i = 0, k = 0; (i < plen) && (prime[i] <= temp); i++) {
        if (mm % prime[i] == 0) {
            factor[k++] = prime[i];
            while (mm % prime[i] == 0) {
                mm /= prime[i];
            }
        }
    }
    if (mm > 1) {
        factor[k++] = mm;
    }
    memset(cfactor, 0, sizeof(cfactor));
    for (i = 2, res0 = 1, res = 1; i <= n; i++) {
        temp = 4 * i - 2;
        for (j = 0; j < k; j++) {
            while (temp % factor[j] == 0) {
                temp /= factor[j];
                cfactor[j]++;
            }
        }
        res0 = res0 * temp % m;
        temp = i + 1;
        for (j = 0; j < k; j++) {
            while (temp % factor[j] == 0) {
                temp /= factor[j];
                cfactor[j]--;
            }
        }
        if (temp > 1) {
            extend_gcd(temp, m);
            x = (x % m + m) % m;
            res0 = res0 * x % m;
        }
        res1 = res0;
        for (j = 0; j < k; j++) {
            if (cfactor[j] > 0) {
                res1 = res1 * modular_exp(factor[j], cfactor[j], m) % m;
            }
        }
        res = (res + res1) % m;
    }
    printf("%I64d\n", res);
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("data.in", "r", stdin);
#endif
    init();
    int n, m;
    while (scanf("%d %d", &n, &m) != EOF,n || m) {
        if (m == 1) {
            puts("0");
            continue;
        }
        solve(n, m);
    }
    return 0;
}