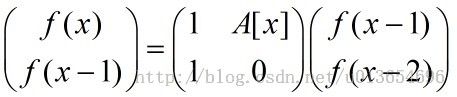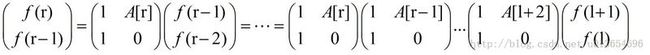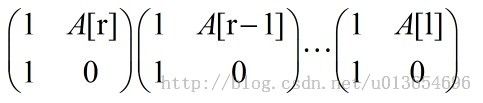ZOJ3772 - Calculate the Function(线段树+矩阵)
题目大意
给定一个序列A1 A2 .. AN 和M个查询
- 每个查询含有两个数 Li 和Ri.
- 查询定义了一个函数 Fi(x) 在区间 [Li, Ri] ∈ Z.
- Fi(Li) = ALi
- Fi(Li + 1) = A(Li + 1)
- 对于所有的x >= Li + 2, Fi(x) = Fi(x - 1) + Fi(x - 2) × Ax
求Fi(Ri)
题解
普通的做法就是每查询一次线性计算一次上式,时间复杂度O(n),所以总的时间复杂度为O(m*n),显然要跪。。。线段树就很好的解决了这个问题,每个结点保存的都是一个矩阵,这样查询的时候就只需要O(logn)的时间了!
代码:
#include <iostream> #include <string> #include <cstring> #include <stdio.h> using namespace std; #define maxn 100005 #define MOD 1000000007 #define lson l,m,s<<1 #define rson m+1,r,s<<1|1 typedef long long LL; struct Matrix { LL mat[2][2]; int r; void init(int n) { memset(mat,0,sizeof(mat)); r=n; } }; Matrix matrix_mul(Matrix a,Matrix b) { Matrix ans; ans.init(a.r); for(int i=0; i<a.r; i++) for(int j=0; j<a.r; j++) for(int k=0; k<a.r; k++) if(a.mat[i][k]&&b.mat[k][j]) ans.mat[i][j]=(ans.mat[i][j]+a.mat[i][k]*b.mat[k][j])%MOD; return ans; } LL a[maxn]; Matrix sum[maxn<<2]; void Pushup(int s) { sum[s]=matrix_mul(sum[s<<1|1],sum[s<<1]); } void build(int l,int r,int s) { sum[s].init(2); if(l==r) { sum[s].mat[0][0]=sum[s].mat[1][0]=1; sum[s].mat[0][1]=a[r]; return; } int m=(l+r)>>1; build(lson); build(rson); Pushup(s); } Matrix query(int ql,int qr,int l,int r,int s) { if(ql<=l&&r<=qr) return sum[s]; int m=(l+r)>>1; Matrix ret; ret.init(2); ret.mat[0][0]=ret.mat[1][1]=1; if(qr>m) ret=matrix_mul(ret,query(ql,qr,rson)); if(ql<=m) ret=matrix_mul(ret,query(ql,qr,lson)); return ret; } int main() { int T; scanf("%d",&T); while(T--) { int n,m; scanf("%d%d",&n,&m); for(int i=1; i<=n; i++) scanf("%lld",&a[i]); build(1,n,1); while(m--) { int l,r; scanf("%d%d",&l,&r); if(l==r||(l+1)==r) { printf("%lld\n",a[r]); continue; } Matrix ans=query(l+2,r,1,n,1); //printf("%I64d %I64d\n",ans.mat[0][0],ans.mat[0][1]); // printf("%I64d %I64d\n",ans.mat[1][0],ans.mat[1][1]); printf("%lld\n",(ans.mat[0][0]*a[l+1]+ans.mat[0][1]*a[l])%MOD); } } return 0; }