算法导论 第7章 课后习题
7.2-4 银行经常按照交易时间,来记录有关某一账户的交易情况,但是,很多人喜欢按照票据号来收到其银行对账单。因此,如何将按交易时间排序转换成按支票编号来排序,就成为一个对几乎排好序的输入进行排序的问题。证明在这个问题上,过程INSERT-SORT的性能往往优于过程QUIKSORT。
问题解析:
对于QUIKSORT来说,输入一个已排序的数组属于最坏的情况,则每次区间划分都是最大程度的不对称。其算法运行的递归时间为T(n) = T(n-1) + Θ(n), 算法时间复杂度为Θ(n^2); 而对INSERT-SORT来说,输入一个已排序的数组却属于最佳的情况,算法时间复杂度为O(n)。也就是说当输入一个几乎排好序的数组,快速排序趋于最坏的情况,而插入排序却趋于最佳的情况。为降低这种最坏情况出现的概率,采用快速排序随机化版本,期望的运行时间为O(nlgn)。
7.3-2 在过程RANDOMIZED-QUIKSORT的运行过程中,最坏情况下对随机排序产生器RANDOM调用了多少次?最佳情况下调用了多少次?以Θ记号形式个给出你的答案。
问题分析:
随机快速排序中,只要区间包含元素数目大于1,则需调用RANDOMIZED-PARTITION,选取主元(pivot)进行区间划分, 而主元的选取需调用Random。主元(pivot)一旦被选出来后,就不会在加入到后续的排序了。直白来说就是,有多少次主元(pivot)选取就有多少次随机数生成。另一方面从算法的递归二叉树树上来看,递归树二叉树的非叶子节点可表示一个主元(pivot);而叶子节点分为两种,一种节点是包含0个元素,另一种节点是包含1个元素,而且该元素不是主元(pivot)。非叶子节点和包含1个元素的叶子节点的数目之和就是输入序列的大小n。即递归树的非叶子节点的数目就是调用RANDOM的次数。调用RANDOM次数T(RANDOM)≤n,即T(RANDOM)=O(n)。
又根据二叉树的性质,
对于任意一棵二叉树,如果其叶结点数为a,而度数为2的结点(非叶子节点)总数为b,则a=b+1;对于快速排序的递归二叉树中,
非叶子节点度数均为2。假设含有0个元素的叶子节点数目a0(≥0),含有1个元素的叶子节点数目为a1,所以 b =a-1 ≥ a1 - 1;又b+a1 = n,可得 b ≥ n/2 - 1
,即T(RANDOM)=Ω(n)。
总的来说T(RANDOM)=
Θ(n)
思考题:
7-3 Howard、Fine等教授提出了下面的“漂亮的”排序算法。
STOOGE-SORT(A, i, j)1 if A[i]>A[j]
2 then exchange A[i]<->A[j]
3 if i+1>=j
4 then return
5 k<-floor((j-i+1)/3)
6 STOOGE-SORT (A, i, j-k)
7 STOOGE-SORT (A, i+k, j)
8
STOOGE-SORT(A, i, j-k)
a) 证明:如果n=Length[A],那么STOOGE-SORT(A, 1, Length[A])能正确地对输入数组A[1..n]进行排序。
b) 给出一个表达STOOGE-SORT最坏情况的运行时间的递归式,以及关于最坏情况运行时间的一个紧确的渐进(Θ记号)界。
a).算法分析:
循环不变式:调用
STOOGE-SORT(A, i, j)后,数组A[i...j]已有序。
初始化:当i+1
≥ j,则A[i, j]包含1个或2个元素。通过1和2行的比较和交换,然后直接返回即可。
保持:假设
STOOGE-SORT(A, i, j)内的递归调用
STOOGE-SORT(A, i, j-k)、
STOOGE-SORT(A, i+k, j)、
STOOGE-SORT(A, i, j-k)均满足循环不变式。
对区间A[i...j]进行划分
A1=A[i...i+k-1],
A2 = A[i+k...j-k],
A3=A[j-k+1, j] ,
且
A[i...j-k] = [A1, A2]
A[i+k...j] = [A2, A3]
A[i...j] = [A1, A2, A3]
因为k=floor( (j-i+1)/3 ),所以 3k ≤ j-i+1 ≤ 3k+2 ·····························(1)
length[A1] = length[A3] = k
length[A2] = j-i+1-2k
由(1)式得,k ≤ length[A2] ≤ k+2 ·····························(2)
行6中调用
STOOGE-SORT(A, i, j-k),执行结果是[A1, A2]升序排序,且A1 ≤ A2(表示A2所有元素均大于A1中的元素)。由(2)式中k ≤ length[A2],所以 [A1, A2] 的k个最大值一定在A2中。由此推知,
[A1, A2, A3]的k个最大值一定在
[A2, A3]中。
行7中调用
STOOGE-SORT(A, i+k, j),执行结果是[A2, A3]升序排序 ,且A2 ≤ A3(表示A3所有元素均大于A2中的元素), A3包含 [A2, A3]的k个最大值。结合对
行6的分析可得,A3包含
[A1, A2, A3]的k个最大值,
A1 ≤ A3 and
A2 ≤ A3。
行8中调用
STOOGE-SORT
STOOGE-SORT(A, i, j-k)类似对
行6的分析可得
A1 ≤ A2。
所以
A1 ≤ A2
≤ A3,且
A1、A2、
A3数组内部已有序。所以
[A1, A2, A3](即A[i...j])已有序。
终止:
STOOGE-SORT(A, 1, n) 执行完后,可使数组 A 有序,算法是正确的。
b).复杂度分析:
可推得
STOOGE-SORT递归式为:
T(n) = 3T(2*k) + O(1),k=floor( n/3 )
忽略边界条件可得,
T(n) = 3T(2n/3) + c
由
主定理可得
a = 3 , b = 3/2, f(n) = c
满足主定理第一种情况,所以T(n) = Θ(n^log(2/3, 3))
7.4 7.1节中的QUICKSORT算法包含有两个对自身递归调用。在调用PARTITION后,左边的子数组和右边的子数组分别被递归排序。
QUICKSORT中第二次递归调用并不是必须的;可以用迭代控制结构来代替它。这种技术称作尾递归,对多数的编译程序都加以了采用。
考虑下面合格快速排序的版本,它模拟了尾递归:
QUICKSORT'(A, p, r)
1 while p < r
2 do ▸ Partition and sort left subarray.
3 q ← PARTITION(A, p, r)
4 QUICKSORT'(A, p, q - 1)
5 p ← q + 1
a)论证QUICKSORT'(A, 1, length[A])能正确地对数组A进行排序。
b)请给出一种在含有n个元素的输入数组上QUICKSORT'的栈深度为Θ(n)的情况。
c)修改QUICKSORT'的代码,使其最坏情况下栈深度为Θ(lgn),保持算法的O(nlgn)期望运行时间不变。
a) 省略
b)问题分析: 由于 QUICKSORT'只是将一般快速排序算法中 第二次递归调用替换为迭代控制结构, 并未改变区间的划分方式。 迭代控制结构(while)不断对左侧区间进行递归调用,对右侧区间进行再次划分,循环往复,直到右侧区间为空或只剩包含1个元素。
设
QUICKSORT'(A, p, r)
算法迭代深度为D(A[p…r]). 且
while
循环一共运行了m次(即在m次循环后q
≥r)
。在while循环迭代中 r 值一直不变, 设第i次循环开始时p=pi,
PARTITION选取的主元为q=
qi。由
行5可得
pi
= qi-1 + 1。令
q
0
= p - 1。
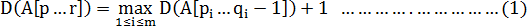
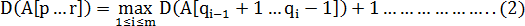
入栈操作是由于左侧区间的递归调用,为使
栈深度趋于Θ(n),就需要左侧区间不断的递归调用
Θ(n)次
。
输入
已升序
排序
数组A[p...r],每次区间划分都是主元(pivot)为A[r],左侧区间为A[p...r-1],右侧区间为空,所以在
QUICKSORT'中的while只循环一次。由(2)式可推得
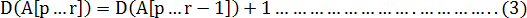
由递归式(3)可知
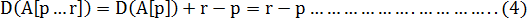
输入数组A为含有n个元素且已按升序排序,栈深度为
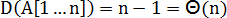
c)问题分析
为保证最坏情况下栈深度为Θ(lgn),即在最坏情况下
左侧区间连续的递归调用
趋近于Θ(lgn)
次。如果每次划分都是最均衡的划分,左侧区间不可能大于n/2,
递归的栈深度最多为Θ(lgn)。为保证每次划分都是均衡的划分,即每次PARTITION选取的主元(pivot)均为区间的中位数即可。