###《Video Event Detection by Inferring Temporal Instance Lables》

论文作者：Kuan-Ting Lai, Felix X. Yu, Ming-Syan Chen and Shih-Fu Chang.

#@author:       gr
#@date:         2014-01-25
#@email:        [email protected]

一、 论文主要工作

1.1 传统方法

传统方法将整个视频表示为一个向量。这种方法简单高效。
一般可以分为如下三个步骤：

• 特征提取(extract features)
  
• 量化(quantized)
  
• 池化(pooling),生成一个全局向量

存在的问题：在最后池化的时候，丢失了时空局部信息。

1.2 主要工作

把一个视频表示为多个实例，这些实例是视频的不同时间间隔。
我们的目标就是学习一个基于实例的事件检测模型。
论文的主要工作：

• 提出一个基于实例的视频检测方法。
  
• 提出的方法可以同时推理实例标签，训练分类模型。
  
• 做了许多实验，证明了算法的性能。

二、提出的方法

2.1 例子

　　　　　　　　　

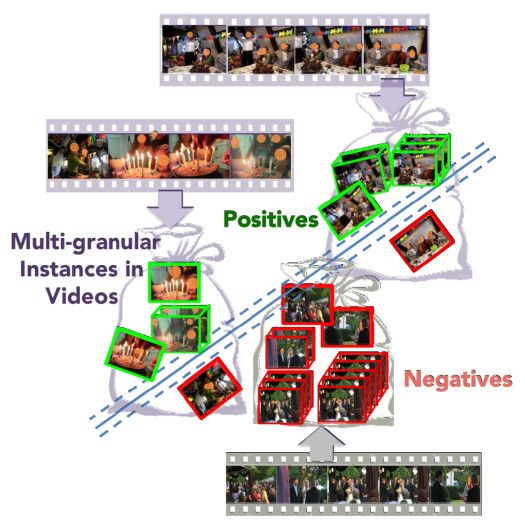
例子： 上面检测视频中是否包含生日聚会，首先将视频划分为许多小的实例。如果较多的实例是与生日聚会相关的，就认为是生日聚会；如果包含没有或较少的实例与生日聚会相关，则说明不包含生日聚会。

2.2 基本表示

${V_m}_{m=1}^M$ 表示数据集中的1到M个视频。

视频 $V_m$ 中含有 $N_m$ 个实例表示为 {x_i^m, y_i^m}_i = 1^N_m 。

其中，$x_i^m$ 表示视频m的第i个实例的特征向量。

2.3 实例比例事件识别

$$p_m(y^m) = \frac{\Sigma_{i=1}^{N_m}I(y_i^m = 1)}{N_m}$$

可以得到目标函数：

$$\min_{\{y^m\}_{m=1}^{M}, w, b} ~~ \frac{1}{2}\parallel w \parallel^2 + C \sum_{m=1}^M \sum_{i=1}^{N_m} L(y_i^m, (w^T x_i^m + b)) \\ s.t. ~~~~ p_m(y^m) = P_m, m = 1,...,M.$$

其中，$L(\cdot)$是经验损失函数。这篇文章中选择 hinge loss function 作为损失函数。

2.4 未知比例

上面讨论的是在 {P_m}_m = 1^M 已知的情况，但实际上，我们只知道视频的标签{Y_m}_m = 1^M，它只能取{ − 1, 1}。

要解决这个问题，我们就设想正例视频中包含更多正实例，负例视频包含较少或没有正实例。

修改后的目标函数：

$$ \begin{aligned} \min_{\{y^m\}_{m=1}^M, w, b} ~~~ \frac{1}{2}\parallel w \parallel^2 & + ~~ C \sum_{m=1}^M \sum_{i=1}^{N_m} L(y_i^m, (w^T x_i^m + b)) \\ & + ~~ C_p\sum_{m=1}^M\mid p_m(y^m) - P_m \mid \end{aligned} $$

$$s.t. ~~~~ P_m = \left\{ \begin{aligned} & 1 ~~~~ if ~~ Y_m = 1 \\ & 0 ~~~~ if ~~ Y_m = -1 \end{aligned} \right. , m = 1, ..., M. $$

其中，第三项是损失函数，惩罚目标正实例比例$P_m$与估计比例$p_m(y^m)$的差别。$C_p$通过交叉验证得出。

2.5 多粒度的实例方法

不同实例的时间不一样。比如，生日聚会可能包含蛋糕和蜡烛，这只需要一帧就能表示；而跑酷就需要视频块才能很好地描述。

假设有K个粒度。第m个视频第k个粒度的实例总数记为$N_k^m$。

定义一个标签向量 y_k^m = [(y₁)_k^m, ⋯, (y_Nk^m)_k^m]。其中，(y_i)_k^m是第m个视频中第k个粒度第i个实例的标签。第k个粒度的权重记为t_k。

$$ p_m(y_1^m \cdots y_K^m) = \dfrac{\sum_{K=1}^{K}t_k(1^T y_k^m)}{2\sum_{k=1}^K t_k N_k^m} + \dfrac{1}{2} $$

目标函数最终形式：

$$ \left. \begin{aligned} \min_{\{y^m\}_{m=1}^M , w, b} \dfrac{1}{2}\parallel w \parallel ^2 + C_p\sum_{m=1}^M \mid p_m(y_1^m \cdots y_K^m) - P_m \mid \\ + C\sum_{m=1}^M \sum_{k=1}^K \sum _{i=1}^{N_k^m} t_k L((y_i)_k^m, (w^T(x_i)_k^m + b)) \\ \end{aligned} \right. $$

$$ s.t. P_m = \left\{ \begin{aligned} & 1 ~~~~ if ~~ Y_m = 1 \\ & 0 ~~~~ if ~~ Y_m = -1 \end{aligned} \right. , m = 1, ..., M. $$

上面的这个问题是个NP难度问题，不能在多项式时间求解。

2.6 优化过程

可以分为下面两种情况分别求解：

• 固定${y^m}_{m=1}^M$,求解$w, b$。这就变成了一个带权重的SVM。

$$ \min_{w, b} \dfrac{1}{2} \parallel w \parallel ^2 + C \sum_{m=1}^M \sum_{k=1}^K \sum_{i=1}^{N_k^m} t_k L((y_i)_k^m, (w^T(x_i)_k^m + b))$$

• 固定$w, b$，更新实例标签${y^m}_{m=1}^M$，问题变成如下：

$$ \left. \begin{aligned} \min_{\{y_m\}_{m=1}^M} C \sum_{m=1}^M \sum_{k=1}^K \sum_{i=1}^{N_k^m} t_k L((y_i)_k^m, (w^T(x_i)_k^m + b)) \\ + C_p\sum_{m=1}^M \mid p_m(y_1^m \cdots y_K^m) - P_m \mid \end{aligned} \right. $$

三、实验结果

3.1 实验设置

在三个视频数据集上进行实验：

• TRECVID Multimedia Event Detection(MED)2011
  
• TRECVID Multimedia Event Detection(MED)2012
  
• Columbia Consumer Videos(CCV)

选取\textbf{SIFT}作为底层局部特征。

对于每个视频，每2s提取一帧，每帧缩放到 $320 \times 240$ 大小。

代价参数 $C$ 和 $C_p$ 通过交叉验证从 ${0.01, 0.1, 1, 10, 100}$ 中选取。

3.2 CCV 上的结果

3.3 MED11 上的结果

　　　　　　　　　　　　　

3.4 MED12 上的结果

四、Reference

1. 项目主页
   
2. 论文链接