SGU 313 Circular Railway
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=313
题意:在一个长为L的环形跑道上,有n个X,n个O,他们每个都位于跑道的某个整数位置上。给出每个X和O的坐标,找出一种配对方案(一个X对一个O),使得每个X到自己的O那里所经过的长度之和最短。输出每个X配对的是第几个O。
思路:如果不是一个环而是一个直线的话,贪心,直接O(n)扫一遍,像括号匹配一样就行了。所以现在的问题就是要找一个分割点,从这个分割点分割开后再对形成的一条直线进行上述操作。首先证明对最优方案时环上必定存在一段弧不被任何一条匹配线覆盖。那么就可以从这条弧上切开成为一条直线。证明如下:对下面这个图,必定不是最优方案。其实可以对所有交叉的匹配进行调整,使得调整后肯定不比原来差:比如XXOO,1和3连,2和4连,我们把它调整成1和4连,2和3连。 假设最优方案没有分割点,那么调整之后答案不变,但是必有一条最长的匹配已经包围了整个环了,这显然是不对的。所以得证。
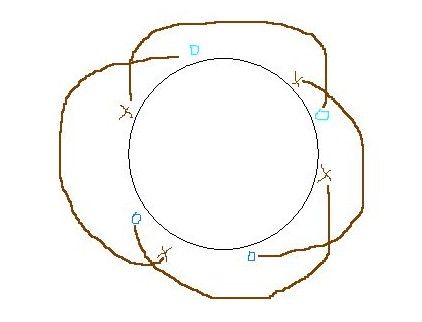
这样的话枚举分割弧是O(n)的,判断O(n),总的复杂度O(n^2)。明显超时。先随便假设一个点为起点(不妨设排序后第一个点)。若以此点所在线段进行分割,那么求得答案就是每条线段长度* 覆盖该弧的匹配边的条数的总和。 覆盖每段弧的匹配边的条数随着分割线的枚举变化是有规律的。扫的过程中,每碰到一个X,匹配线标记+1,碰到O就-1。以XXOOOX为例,一开始每条弧的覆盖数为:1 2 1 0 |-1| 0。那么,当匹配点往后移一位时,相当于是最左边的点移到了最右边,若最左边是X,那么 线段变成了XOOOXX ,新标记就是0 1 0 |-1| |-2| |-1|(注意要保持标记对应的边不变,最右边的X实际上是第一个点,所以改动后最右边->最左边的边即为第1条边),发现所有边的标记都-1。那么,相当于找一个数,让它与所有线段原标记的差绝对值*对应线段长度的值尽量小。
做法如下:首先将XO的坐标放在一起排序,计算每段弧的长度(该数组为b)以及被匹配线覆盖的次数(该数组为c)。然后按照c的升序排序。循环一遍找到最优值,记录最优值出现的位置。从记录的位置扫一遍可得到答案。
struct node
{
int pos,x,y;
node(){}
node(int _pos,int _x,int _y)
{
pos=_pos;
x=_x;
y=_y;
}
};
const int N=100005;
node a[N];
int n,L,aNum,p[N];
int cmp(node a,node b)
{
return a.pos<b.pos;
}
i64 b[N],c[N],d[N],cnt;
int cmp1(int x,int y)
{
return c[x]<c[y];
}
void deal()
{
int i,j,k=0;
FOR1(i,aNum)
{
if(a[i].x==1) k++;
else k--;
b[++cnt]=a[i+1].pos-a[i].pos;
c[cnt]=k;
}
FOR1(i,cnt) d[i]=i;
sort(d+1,d+cnt+1,cmp1);
i64 ans=1e18,temp=0,sum=0,flag;
FOR1(i,cnt) temp+=b[i]*c[i],sum+=b[i];
i64 L=0,t=0;
FOR1(j,cnt)
{
i=d[j];
temp+=L*(c[i]-t)-(sum-L)*(c[i]-t);
if(temp<ans) ans=temp,flag=i;
t=c[i];
L+=b[i];
}
PR(ans);
stack<int> st[2];
for(i=flag+1;;i++)
{
if(i>aNum) i=1;
if(a[i].x==1)
{
if(SZ(st[1]))
{
p[a[i].y]=a[st[1].top()].y;
st[1].pop();
}
else
{
st[0].push(i);
}
}
else
{
if(SZ(st[0]))
{
p[a[st[0].top()].y]=a[i].y;
st[0].pop();
}
else
{
st[1].push(i);
}
}
if(i==flag) break;
}
FOR1(i,n) printf("%d ",p[i]);
puts("");
}
int main()
{
RD(n,L);
int i,pos;
FOR1(i,n)
{
RD(pos);
a[++aNum]=node(pos,1,i);
}
FOR1(i,n)
{
RD(pos);
a[++aNum]=node(pos,2,i);
}
sort(a+1,a+aNum+1,cmp);
a[aNum+1]=a[1];
a[aNum+1].pos+=L;
deal();
return 0;
}