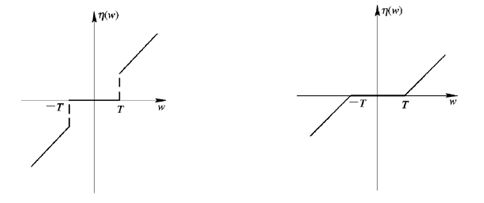【DWT笔记】基于小波变换的降噪技术

 

【DWT笔记】基于小波变换的降噪技术

---

一、前言

     在现实生活和工作中，噪声无处不在，在许多领域中，如天文、医学图像和计算机视觉方面收集到的数据常常是含有噪声的。噪声可能来自获取数据的过程，也可能来自环境影响。由于种种原因,总会存在噪声，噪声的存在往往会掩盖信号本身所要表现的信息，所以在实际的信号处理中，常常需要对信号进行预处理，而预处理最主要的一个步骤就是降噪。

     小波分析是近年来发展起来的一种新的信号处理工具，这种方法源于傅立叶分析，小波（wavelet），即小区域的波，仅仅在非常有限的一段区间有非零值，而不是像正弦波和余弦波那样无始无终。小波可以沿时间轴前后平移，也可按比例伸展和压缩以获取低频和高频小波，构造好的小波函数可以用于滤波或压缩信号，从而可以提取出已含噪声信号中的有用信号。

 

---

 

二、小波去噪的原理

     从信号学的角度看 ,小波去噪是一个信号滤波的问题。尽管在很大程度上小波去噪可以看成是低通滤波 ,但由于在去噪后 ,还能成功地保留信号特征 ,所以在这一点上又优于传统的低通滤波器。由此可见 ,小波去噪实际上是特征提取和低通滤波的综合 ,其流程图如下所示：

     

      一个含噪的模型可以表示如下：

     

     其中 ,f( k)为有用信号,s(k)为含噪声信号,e(k)为噪声,ε为噪声系数的标准偏差。

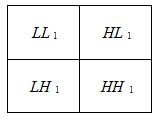
     假设，e(k)为高斯白噪声,通常情况下有用信号表现为低频部分或是一些比较平稳的信号,而噪声信号则表现为高频的信号,我们对 s(k)信号进行小波分解的时候,则噪声部分通常包含在HL、LH、HH中,如下图所示，只要对HL、LH、HH作相应的小波系数处理,然后对信号进行重构即可以达到消噪的目的。

      

     我们可以看到，小波去噪的原理是比较简单类，类似以往我们常见的低通滤波器的方法，但是由于小波去找保留了特征提取的部分，所以性能上是优于传统的去噪方法的。

     

---

三、小波去噪的基本方法

     一般来说， 一维信号的降噪过程可以分为 3个步骤

      信号的小波分解。选择一个小波并确定一个小波分解的层次N，然后对信号进行N层小波分解计算。

      小波分解高频系数的阈值量化。对第1层到第N层的每一层高频系数（三个方向）， 选择一个阈值进行阈值量化处理．

     这一步是最关键的一步，主要体现在阈值的选择与量化处理的过程，在每层阈值的选择上matlab提供了很多自适应的方法， 这里不一一介绍，量化处理方法主要有硬阈值量化与软阈值量化。下图是二者的区别：

     

     上面左图是硬阈值量化，右图是软阈值量化。采用两种不同的方法，达到的效果是，硬阈值方法可以很好地保留信号边缘等局部特征，软阈值处理相对要平滑，但会造成边缘模糊等失真现象。   

      信号的小波重构。根据小波分解的第 N层的低频系数和经过量化处理后的第1层到第N 层的高频系数，进行信号的小波重构。

 

---

 

四、仿真实验

     在这里，我采用lena的256*256的标准图进行分析，采用 coif2的两层小波分解，并从三个方向上对小波系数进行软阈值量化，为了方便起见，阈值的选择我采用手动设定的方法，最后对图像进行小波重构，后面部分会给出重构的效果图和相应的峰值信噪比。代码如下：

 1 clear;  2 clc;  3 X=imread('lena256.bmp');  4 %X=rgb2gray(X);  5 figure(1);  6 subplot(121);  7 imshow(X);  8 title('原始图像');  9 X=double(X); 10 
11 XX=X+10*randn(size(X)); 12 subplot(122); 13 imshow(uint8(XX)); 14 title('含噪图像'); 15 
16  [c,l]=wavedec2(XX,2,'coif2'); 17  
18 n=[1,2]; 19 p=[10.28,10.08]; 20  
21 nc_h=wthcoef2('h',c,l,n,p,'s'); 22 
23 X1=waverec2(nc_h,l,'coif2'); 24 figure(2); 25 subplot(131); 26 imshow(uint8(X1)); 27 title('第一次消噪后的图像'); 28  
29 
30 nc_v=wthcoef2('v',nc_h,l,n,p,'s'); 31 
32 X2=waverec2(nc_v,l,'coif2'); 33 subplot(132); 34 imshow(uint8(X2)); 35 title('第二次消噪后的图像'); 36  
37 
38 nc_d=wthcoef2('d',nc_v,l,n,p,'s'); 39 
40 X3=waverec2(nc_d,l,'coif2'); 41 subplot(133); 42 imshow(uint8(X3)); 43 title('第三次消噪后的图像'); 44  
45 psnr0=psnr(X,XX); 46 psnr1=psnr(X,X1); 47 psnr2=psnr(X,X2); 48 psnr3=psnr(X,X3);

     

 

     下面给出运行的效果图，为了显示方便，我重新排版了下，下图是原图和加噪后的图像：

     

     下面给出去噪的效果图：

     

    信噪比数据为：

 1 psnr0 =
 2    28.1782
 3 
 4 psnr1 =
 5    29.1551
 6 
 7 psnr2 =
 8    30.0441
 9 
10 psnr3 =
11    31.6952

     为了增加实验室可信度，可以写一个简单的基于DCT变换的低通滤波器的去噪的方法，如下所示：

 1 clear;  2 clc;  3 
 4 X=imread('lena256.bmp');  5 %X=rgb2gray(X);  6 figure(1);  7 subplot(141);  8 imshow(X);  9 title('原始图像'); 10 % 生成含噪图像并图示 11 X=double(X); 12 
13 % 添加随机噪声 14 XX=X+10*randn(size(X)); 15 
16 Y1=dct2(XX); 17 
18 [m,n]=size(Y1) 19 for i=1:m 20     for j=1:n 21         if abs(Y1(i,j))<20 %这个阈值要根据实际情况设定
22            Y1(i,j)=0; 23  end 24  end 25 end 26 
27 YY1=idct2(Y1); 28 subplot(142) 29 imshow(uint8(XX)); 30 
31 subplot(143) 32 imshow(uint8(YY1)); 33 
34 psnr0=psnr(X,XX) 35 psnr4=psnr(X,YY1)

      运行的效果图为：

     

      运行的结果为：

1 psnr0 =
2 
3    28.1068
4 
5 
6 psnr4 =
7 
8    28.6162

     由此，我们可以看出，小波变换去噪能力还是比较突出的。

 

---

五、小结

       离散小波变换（DWT）在图像处理中的运用还是十分广泛的，去噪只是其中一个。有时间会跟大家一起总结下其他的应用。

 

 

我的新浪微博：http://weibo.com/3109428257/profile?rightmod=1&wvr=5&mod=personinfo