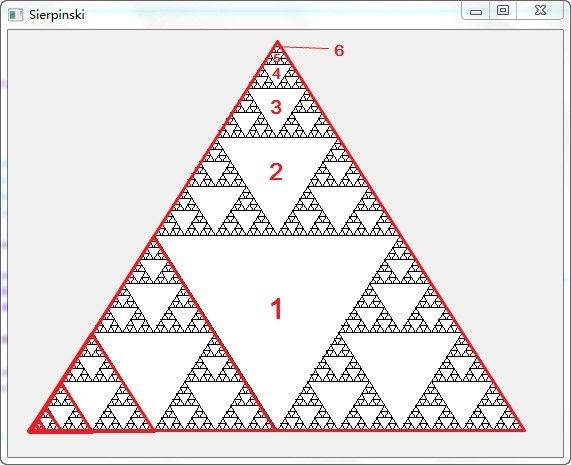
附加实验1 Sierpinski三角形
1.实验目的:
理解掌握一个OpenGL绘制图形的完整程序结构。
2.实验内容:
(1) 运行示范实验代码,掌握程序结构与每一个语句含义;
(2) 了解分形图形的生成特点,并能将其扩展、举一反三。
3.实验原理:
Sierpinski三角形是一种分形图形,它是递归地构造的。最常见的构造方法如下图所示:把一个三角形分成四等份,挖掉中间那一份,然后继续对另外三个三角形进行这样的操作,并且无限地递归下去。每一次迭代后整个图形的面积都会减小到原来的3/4,因此最终得到的图形面积显然为0。这也就是说,Sierpinski三角形其实是一条曲线。
图1
大概在下图上标注了一下一个三角形迭代过程:
图2
生成Sierpinski 三角形算法描述,如图1所示:
(1)从一个三角形开始;
(2)连接三边的中点并去掉中间的三角形;
(3)重复上述过程;
4.示范代码:
#include <GL/glut.h>
// a point data type
typedef GLfloat point2d[2];
//initial triangle
point2d v[3] = {{-1.0, -0.58}, {1.0, -0.58}, {0.0, 1.15}};
int n; // number of recursive steps
// display one triangle
void triangle( point2d a, point2d b, point2d c)
{
glBegin(GL_TRIANGLES);
glVertex2fv(a);
glVertex2fv(b);
glVertex2fv(c);
glEnd();
}
// triangle subdivision using vertex numbers
void divide_triangle(point2d a, point2d b, point2d c, int m) {
point2d v0, v1, v2;
int j;
if(m>0) {
for(j=0; j<2; j++) v0[j]=(a[j]+b[j])/2;
for(j=0; j<2; j++) v1[j]=(a[j]+c[j])/2;
for(j=0; j<2; j++) v2[j]=(b[j]+c[j])/2;
divide_triangle(a, v0, v1, m-1);
divide_triangle(c, v1, v2, m-1);
divide_triangle(b, v2, v0, m-1);
}
else(triangle(a,b,c));// draw triangle at end of recursion
}
void mydisplay(void) {
glClear(GL_COLOR_BUFFER_BIT);
divide_triangle(v[0], v[1], v[2], n);
glFlush();
}
void init() {
glClearColor(1.0, 1.0, 1.0,1.0);
glColor3f(0.0,0.0,0.0);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(-2.0, 2.0, -2.0, 2.0, -1.0, 1.0);
}
void main(int argc, char **argv)
{
n=1;
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);
glutInitWindowSize(500, 500);
glutInitWindowPosition(50,50);
glutCreateWindow("2D Sierpinski");
glutDisplayFunc(mydisplay);
init();
glutMainLoop();
}
4. 实验作业:
请参考上述代码实现Koch曲线或Koch雪花的生成。
Koch曲线:
Koch雪花:
可参考如下资料:
(1).http://hi.baidu.com/zotin/item/f67aaadb9411934edcf9be6e;