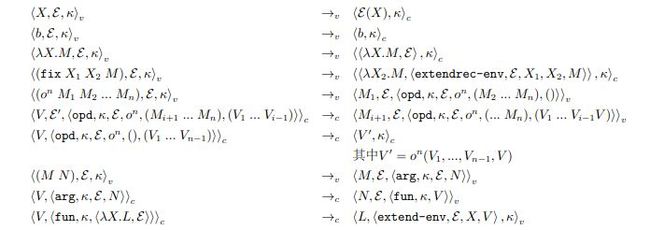简单易懂的程序语言入门小册子(9):环境,引入环境
\[\newcommand{\mt}[1]{\text{#1}} \newcommand{\mE}{\mathcal{E}} \newcommand{\tup}[1]{\left<{#1}\right>}\]
环境类似于其他语言(C++、JAVA等)的“符号表”。 所谓符号表,是一张将变量名与变量代表的内容联系起来的一张表。 不过这里我们抛弃符号表的观点,单纯地从算法角度上引入环境这一概念。
引入环境
通过修改解释器求值过程的算法,可以很自然的引入环境这个概念。
在前面基于文本替换的解释器里可以看到,所谓的“计算”,其实不过是一堆符号根据某种规则替换来替换去最终得到一个不能再归约的结果的过程。 这个替换过程需要遍历表达式。 比如计算表达式$(\lambda X.M \; V)$,需要进行替换$M[X \leftarrow V]$。 这个替换过程需要遍历表达式$M$。 而求值过程本身也需要遍历表达式$M$。 这样就至少需要遍历两次表达式$M$。 另外,替换过程本身也很麻烦,其中有这么一条规则: \begin{equation*}\begin{array}{lcl} (\lambda X_1.M)[X_2 \leftarrow N] &=& (\lambda X_3.M[X_1 \leftarrow X_3][X_2 \leftarrow N]) \\ && \begin{array}{ll} \text{其中} & X_1 \neq X_2, X_3 \notin FV(N), \\ & X_3 \notin FV(M)\backslash\{X_1\} \end{array} \end{array}\end{equation*} 在这种情况下,一次替换要遍历两次$M$。
这样一来,在原来的算法里,由于直接使用替换,计算一个表达式需要一遍遍地遍历这个表达式的子表达式们。 这是一个效率很低的方法。 为了避免这些多余的遍历过程,我们可以延后替换过程,等到遍历到需要替换的变量时再对这个变量做替换。 这样只需要一次遍历就够了。 为了延后替换过程,需要一个保存这些“延后的替换”的数据结构。 这个数据结构叫做环境。 我们用字母$\mE$表示环境。
下面举个例子来粗略地说明如何用环境来进行计算(粗略的展示,不代表实际的计算步骤): \begin{equation*}\begin{array}{lcl} && (\underline{(\lambda x.\lambda y.(+ \; x \; y) \; 11)} \; 22) \\ &\rightarrow& \underline{(\tup{\lambda y.(+ \; x \; y), \tup{(x \leftarrow 11)}} \; 22)} \\ &\rightarrow& \underline{\tup{(+ \; x \; y), \tup{(y \leftarrow 22), (x \leftarrow 11)}}} \\ &\rightarrow& \tup{\underline{(+ \; 11 \; 22)}, \tup{(y \leftarrow 22), (x \leftarrow 11)}} \\ &\rightarrow& \tup{\underline{33}, \tup{(y \leftarrow 22), (x \leftarrow 11)}} \\ &\rightarrow& 33 \end{array}\end{equation*}
引入环境后,一个表达式就可能不是一个“完整的表达式”了。 因为这个表达式可能有些自由变量应该被替换,只是替换被延后了,所以它看起来仍保持还没被替换的样子。 所以,一个“完整的表达式”,应该包括表达式和“延后的替换”的信息——也就是环境。 表达式和环境这个二元组叫做闭包,记为$\tup{M, \mE}$。
我一直故意没有描述环境的具体定义。 有了闭包这个概念后,现在可以说说环境的定义了。 从用途上看,环境可以理解成一个函数,它的输入是一个变量,它的输出是这个变量应该被替换成的东西。 这个“被替换成的东西”是什么东西呢? 一个直接的想法是表达式。 但这是不正确的! 因为一个表达式可能不是一个“完整的表达式”。 所以这个“被替换成的东西”应该是一个闭包。 也就是说,环境是一个将变量映射成闭包的函数: \[ \mE: X \rightarrow \tup{M, \mE} \] 为什么定义环境这么麻烦? 因为它是个递归定义。 考虑上闭包的话,环境和闭包就是互递归定义。
构造环境
考虑表达式$(\mt{let} \; a \; 1 \; (\mt{let} \; a \; 2 \; a))$。 这个表达式共有两次替换,第一次将变量$a$替换成$1$,第二次将变量$a$替换成$2$,而表达式最终的值是$2$。 可以看到,当遇到同名变量时,后替换的变量有效。 用于保存替换信息的环境应该具有后进入先找到(栈!)的性质。 环境可以用链表的形式保存。 每次保存替换信息时,将要替换的变量和应该替换成的闭包插入到链表的头部; 而查找是从头部开始查找。
构造环境的方法如下面公式所示: \begin{equation*}\begin{array}{lcl} \mE &=& \mt{empty-env} \\ &|& \tup{\mt{extend-env}, \mE, X, \tup{M, \mE'}} \end{array}\end{equation*} $\mt{empty-env}$表示空环境。 空环境没有保存任何的“延后的替换”。 由于空环境表示没有替换,所以对空环境输入任何变量$X$,它的输出是个包含$X$的闭包$\tup{X, \mt{empty-env}}$ (另一种处理方式是输出错误“未定义/无绑定的变量$X$”)。 $\mt{extend-env}$这一行扩展了原来的环境,这个构造过程称为将变量$X$绑定到闭包$\tup{M, \mE'}$。
当输入变量$X$时,从链表的头部开始搜索,返回第一次找到变量$X$时对应的闭包。 用$\mE(X)$表示在环境$\mE$中查找$X$的过程,这个过程如下: \begin{equation*}\begin{array}{lcl} \mt{empty-env}(X) &=& \tup{X, \mt{empty-env}} \\ \tup{\mt{extend-env}, \mE, X, \tup{M, \mE'}}(X) &=& \tup{M, \mE'} \\ \tup{\mt{extend-env}, \mE, X', \tup{M, \mE'}}(X) &=& \mE(X) \\ && \text{其中} X' \neq X \end{array}\end{equation*}
CEK machine
还记得CK machine吗? CEK machine指的是加入环境后的CK machine。
为了简化问题,暂时先不考虑递归表达式$(\mt{fix} \; X_1 \; X_2 \; M)$。 无fix表达式的Alligator的语法(我真的没在凑字数): \begin{equation*}\begin{array}{lcl} M, N, L &=& X \\ &|& b \\ &|& \lambda X.M \\ &|& (+ \; M \; N) \\ &|& (- \; M \; N) \\ &|& (\mt{iszero} \; M) \\ &|& (M \; N) \\ \end{array}\end{equation*}
CEK machine的求值过程从CK machine的求值过程稍微改改得到。 无fix表达式的Alligator的语法中只有函数调用$(M \; N)$会用到替换。 现在我们不使用替换,取而代之的是扩展环境。 其他的改动还有:原来的表达式$M$改成闭包$\tup{M, \mE}$; 而变量$X$现在要到环境查找对应的闭包$\mE(X)$。 另外,Alligator使用call-by-value的调用顺序,所以要求环境值域的闭包里的表达式是一个值。 也就是说,CEK machine里用到的环境应该是这样的函数: \[ \mE: X \rightarrow \tup{V, \mE} \] 新的求值过程如下(可以对比一下CK machine的求值过程)(公式太多mathjax出问题只好不得不截图……):
递归的处理
fix表达式的求值过程需要特别的处理。 按照上面的技巧修改fix表达式的求值过程,这个求值过程有如下形式: \[ \tup{\tup{(\mt{fix} \; X_1 \; X_2 \; M), \mE}, \kappa}_v \rightarrow_v \tup{\tup{\lambda X_2.M, \mE^{fix}}, \kappa}_c \] 关键是$\mE^{fix}$是什么? 由于$\lambda X_2.M$还有自由变量$X_1$,所以$\mE^{fix}$是在$\mE$基础上将变量$X_1$绑定到代表这个递归函数的闭包。 这个闭包是$\tup{\lambda X_2.M, \mE^{fix}}$。 所以$\mE^{fix}$满足下面这个方程: \[ \mE^{fix} = \tup{\mt{extend-env}, \mE, X_1, \tup{\lambda X_2.M, \mE^{fix}}} \] 这个方程是没法解出来咯。 只能换个方式来得到$\mE^{fix}$。 直接扩展构造环境的方法: \begin{equation*}\begin{array}{lcl} \mE &=& ... \\ &|& \tup{\mt{extendrec-env}, \mE, X_1, X_2, M} \end{array}\end{equation*} 由$\mt{extendrec-env}$方式扩展的环境在查找变量$X$时的行为如下: \begin{equation*}\begin{array}{lcl} \tup{\mt{extendrec-env}, \mE, X, X_2, M}(X) &=& \tup{\lambda X_2.M, \tup{\mt{extendrec-env}, \mE, X, X_2, M}} \\ \tup{\mt{extendrec-env}, \mE, X_1, X_2, M}(X) &=& \mE(X) \\ && \text{其中} X_1 \neq X \end{array}\end{equation*}
增加了构造环境方法后,fix表达式的求值过程如下: \[ \tup{\tup{(\mt{fix} \; X_1 \; X_2 \; M), \mE}, \kappa}_v \rightarrow_v \tup{\tup{\lambda X_2.M, \tup{\mt{extendrec-env}, \mE, X_1, X_2, M}}, \kappa}_c \]
代码实现
写代码咯,首先,用Racket的结构来表示闭包:
环境的代码,同样用结构来表示环境:
函数$\mt{apply-env}$是在环境中查找变量的过程:
最后是求值过程的代码:
简化CEK machine
CEK machine里环境的值域只有三种类型的闭包: 包含变量的闭包$\tup{X, \mt{empty-env}}$、 包含常数的闭包$\tup{b, \mE}$ 以及包含函数的闭包$\tup{\lambda X.M, \mE}$。 这三种闭包只有函数的情况需要环境。 而变量和常数的情况下不需要环境。 修改值类型为: \begin{equation*}\begin{array}{lcl} V &=& X \\ &|& b \\ &|& \tup{\lambda X.M, \mE} \end{array}\end{equation*} 我们一直以来将值当作一种特殊的表达式,也就是说值是表达式的子集。 而修改后的值类型已经不是表达式的子集了。
修改环境的定义,将环境的定义改为变量到值的映射: \[ \mE: X \rightarrow V \] 构造环境的方法: \begin{equation*}\begin{array}{lcl} \mE &=& \mt{empty-env} \\ &|& \tup{\mt{extend-env}, \mE, X, V} \\ &|& \tup{\mt{extendrec-env}, \mE, X_1, X_2, M} \end{array}\end{equation*} 求值过程的简化主要是去掉一些不必要的闭包的构造。 简化后的求值过程如下: \begin{equation*}\begin{array}{lcl} \tup{X, \mE, \kappa}_v &\rightarrow_v& \tup{\mE(X), \kappa}_c \\ \tup{b, \mE, \kappa}_v &\rightarrow_v& \tup{b, \kappa}_c \\ \tup{\lambda X.M, \mE, \kappa}_v &\rightarrow_v& \tup{\tup{\lambda X.M, \mE}, \kappa}_c \\ \tup{(\mt{fix} \; X_1 \; X_2 \; M), \mE, \kappa}_v &\rightarrow_v& \tup{\tup{\lambda X_2.M, \tup{\mt{extendrec-env}, \mE, X_1, X_2, M}}, \kappa}_c \\ \tup{(o^n \; M_1 \; M_2 \; ... \; M_n), \mE, \kappa}_v &\rightarrow_v& \tup{M_1, \mE, \tup{\mt{opd}, \kappa, \mE, o^n, (M_2 \; ... \; M_n), ()}}_v \\ \tup{V, \mE', \tup{\mt{opd}, \kappa, \mE, o^n, (M_{i+1} \; ... \; M_n), (V_1 \; ... \; V_{i-1})}}_c &\rightarrow_c& \tup{M_{i+1}, \mE, \tup{\mt{opd}, \kappa, \mE, o^n, (... \; M_n), (V_1 \; ... \; V_{i-1} V)}}_v \\ \tup{V, \tup{\mt{opd}, \kappa, \mE, o^n, (), (V_1 \; ... \; V_{n-1})}}_c &\rightarrow_c& \tup{V', \kappa}_c \\ && \text{其中} V' = o^n(V_1, ..., V_{n-1}, V) \\ \tup{(M \; N), \mE, \kappa}_v &\rightarrow_v& \tup{M, \mE, \tup{\mt{arg}, \kappa, \mE, N}}_v \\ \tup{V, \tup{\mt{arg}, \kappa, \mE, N}}_c &\rightarrow_c& \tup{N, \mE, \tup{\mt{fun}, \kappa, V}}_v \\ \tup{V, \tup{\mt{fun}, \kappa, \tup{\lambda X.L, \mE}}}_c &\rightarrow_c& \tup{L, \tup{\mt{extend-env}, \mE, X, V}, \kappa}_v \end{array}\end{equation*} 代码实现:略。
思考
- 用函数表示环境。
- 关于递归的处理,$\mt{extendrec-env}$的扩展方式可能看起来有点违和感。 使用带有“副作用”的方法可以避免这种扩展方式的使用。修改环境为带有存储的环境(方括号表示这个是一个引用,这个引用指向的存储里的值是$V$): \begin{equation*}\begin{array}{lcl} \mE &=& \mt{empty-env} \\ &|& \tup{\mt{extend-env}, \mE, X, [V]} \end{array}\end{equation*} 另外增加一个修改存储的方法$(\mt{set-value-env!} \; \mE \; V')$, 其中这里的$\mE=\tup{\mt{extend-env}, \mE, X, [V]}$。 这个方法修改环境$\mE$为$\tup{\mt{extend-env}, \mE, X, [V']}$。为了计算fix表达式$(\mt{fix} \; X_1 \; X_2 \; M)$扩展的环境$\mE^{fix}$, 先将$X_1$绑定到一个未初始化的值: \[ \mE^{fix} = \tup{\mt{extend-env}, \mE, X_1, [uninitialized]} \] 其中$uninitialized$表示未初始化。 然后修改$\mE^{fix}$: \[ (\mt{set-value-env!} \; \mE^{fix} \; \tup{\lambda X_2.M, \mE^{fix}}) \] 这样就能得了$\mE^{fix}$。
- 这是一个算法练习。 在一些代码分析过程中,知道代码中所有变量的使用次数是很有用的。 我们希望统计所有变量的使用次数,并标记在变量声明的位置。 例如输入一段代码:
(((lambda x (lambda y (+ ((lambda x x) 33) (+ y (+ x x))))) 11) 22)输出:(((lambda (x 2) (lambda (y 1) (+ ((lambda (x 1) x) 33) (+ y (+ x x))))) 11) 22)如何实现这个算法?要求只遍历代码一次。