每日一“酷”之heapq

作用:heapq模块实现一个适用于Python列表的最小堆排序算法

　　堆（heap）是一个属性数据结构，其中子节点与父节点是一种有序关系。二叉堆是一种特殊的堆，二叉堆是完全二元树（二叉树）或者是近似完全二元树（二叉树）。可以使用以下如下方式组织的列表或数表示，即元素N的子元素位于2*N+1和2*N+2。这种布局允许原地重新组织堆，从而不必再增加或删除元素时分配大量内存。

      最大堆确保父节点大于或等于其两个子节点。最小堆要求父节点小雨或等于其子节点。Python的heqpq模块实现了一个最小堆。

1、示例数据

数据存储在：heapq_heapdata.py中

data = [19,9,4,10,11]

堆的输出存储在heapq_showtree.py 

 1 import math

 2 import cStringIO

 3 

 4 def show_tree(tree,total_width=36,fill=' '):

 5     output = cStringIO.StringIO()

 6     last_row = -1

 7     for i,n in enumerate(tree):

 8         if i :

 9             row = int(math.floor(math.log(i+1,2)))

10         else:

11             row = 0

12         if row != last_row:

13             output.write('\n')

14         columns = 2 ** row

15         col_width = int(math.floor((total_width * 1.0) / columns))

16         output.write(str(n).center(col_width,fill))

17         last_row = row

18     print output.getvalue()

19     print '-' * total_width

20     print 

21     return 

 

2、创建堆

创建堆的两种基本方式：heappush()和heapify() 

 1 import heapq

 2 from heapq_heapdata import data

 3 from heapq_showtree import show_tree

 4 

 5 heap = []

 6 print 'random : ' , data

 7 print 

 8 for n in data:

 9     print 'add %3d:' % n

10     heapq.heappush(heap,n)

11     show_tree(heap)

运行结果：

使用heappush()时，从数据源增加新元素时会保持元素的堆顺序

 

如果数据已经存在内存中，使用heaoify()原地重新组合字列表中的元素会更高效

 

1 import heapq

2 from heapq_heapdata import data

3 from heapq_showtree import show_tree

4 

5 heap = []

6 print 'random : ' , data

7 heapq.heapify(data)

8 print 'heapifed : '

9 show_tree(data)

运行结果：

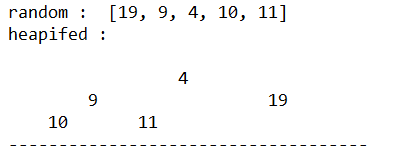
如果按堆顺序一次一个元素构建列表，其结果与构建一个无序列表在调用heapify()是一样的。

 

3、访问堆内容

一旦堆已正确组织，就可以使用heappop()删除有最小值的元素

 1 import heapq

 2 from heapq_heapdata import data

 3 from heapq_showtree import show_tree

 4 

 5 print 'random    :', data

 6 heapq.heapify(data)

 7 print 'heapifed : '

 8 show_tree(data)

 9 print 

10 for i in xrange(2):

11     smallest = heapq.heappop(data)

12     print 'pop       %3d:' % smallest

13     show_tree(data)

运行结果：

这个例子是由stdlib文档改写的，其中使用了heapify()和heappop()对一个数组列表排序。

如果希望在一个操作中删除现有元素并替换新值，可以使用heapreplace()。

 1 import heapq

 2 from heapq_heapdata import data

 3 from heapq_showtree import show_tree

 4 

 5 heapq.heapify(data)

 6 print 'start:'

 7 show_tree(data)

 8 for n in [0,13]:

 9     smallest = heapq.heapreplace(data, n)

10     print 'replace %2d with %3d' % (smallest,n)

11     show_tree(data)

运行结果：

通过原地替换元素，这样可以维持一个固定大小的堆，如按优先级排序的作业队列。

4、堆的数据极值

Heapq还包括两个检查可迭代对象的函数，查找其中包含最大值或最小值的范围

1 import heapq

2 from heapq_heapdata import data

3 print 'all       :',data

4 print '3 largest :',heapq.nlargest(3,data)

5 print 'from sort :',list(reversed(sorted(data)[-3:]))

6 print '3 smallest:',heapq.nsmallest(3,data)

7 print 'from sort :',sorted(data)[:3]

运行结果：

只有当n值（n>1）相对小时使用nlargest()和nsmallest()才算高效，不过有些情况下这两个函数会很方便。