UESTC 33 Area --凸包面积

题意： 求一条直线分凸包两边的面积。

解法： 因为题意会说一定穿过，那么不会有直线与某条边重合的情况。我们只要找到一个直线分成的凸包即可，另一个的面积等于总面积减去那个的面积。

怎么得到分成的一个凸包呢？

从0~n扫过去，如果扫到的边与直线不相交，那么把端点加进新凸包中，如果直线与扫到的边相交了，那么就将交点加入新凸包，然后以后不相交的话也不加入点到新凸包中，直到遇到下一个与直线相交的边，则把交点又加入新凸包，然后在扫到末尾加入点。这样就得到了。

即找到如图：

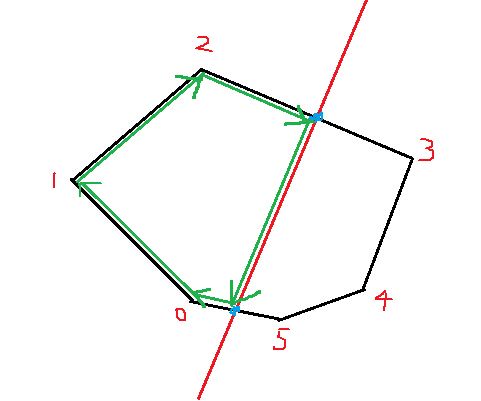
注意四舍五入。

代码：

#include <iostream>

#include <cstdio>

#include <cstring>

#include <cstdlib>

#include <cmath>

#include <algorithm>

#define eps 1e-8

using namespace std;



struct Point{

    double x,y;

    Point(double x=0, double y=0):x(x),y(y) {}

    void input() { scanf("%lf%lf",&x,&y); }

};

typedef Point Vector;

int dcmp(double x) {

    if(x < -eps) return -1;

    if(x > eps) return 1;

    return 0;

}

template <class T> T sqr(T x) { return x * x;}

Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }

Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); }

Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }

Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }

bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y); }

bool operator >= (const Point& a, const Point& b) { return a.x >= b.x && a.y >= b.y; }

bool operator <= (const Point& a, const Point& b) { return a.x <= b.x && a.y <= b.y; }

bool operator == (const Point& a, const Point& b) { return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0; }

double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }

double Length(Vector A) { return sqrt(Dot(A, A)); }

double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }



Point DisP(Point A,Point B) { return Length(B-A); }

bool SegmentIntersection(Point A,Point B,Point C,Point D) {

    return max(A.x,B.x) >= min(C.x,D.x) &&

           max(C.x,D.x) >= min(A.x,B.x) &&

           max(A.y,B.y) >= min(C.y,D.y) &&

           max(C.y,D.y) >= min(A.y,B.y) &&

           dcmp(Cross(C-A,B-A)*Cross(D-A,B-A)) <= 0 &&

           dcmp(Cross(A-C,D-C)*Cross(B-C,D-C)) <= 0;

}

void SegIntersectionPoint(Point& P,Point a,Point b,Point c,Point d) {  //需保证ab,cd相交

    P.x = (Cross(d-a,b-a)*c.x - Cross(c-a,b-a)*d.x)/(Cross(d-a,b-a)-Cross(c-a,b-a));

    P.y = (Cross(d-a,b-a)*c.y - Cross(c-a,b-a)*d.y)/(Cross(d-a,b-a)-Cross(c-a,b-a));

}

double CalcConvexArea(Point* p,int n)

{

    double area = 0.0;

    for(int i=1;i<n-1;i++)

        area += Cross(p[i]-p[0],p[i+1]-p[0]);

    return fabs(area*0.5);

}

Point p[25],ch[25];

Point P,A,B;



int main()

{

    int n,i,m;

    while(scanf("%d",&n)!=EOF && n)

    {

        for(i=0;i<n;i++) p[i].input();

        A.input(), B.input();

        Point tmpA = B+(A-B)*20003, tmpB = A+(B-A)*20003;

        A = tmpA, B = tmpB;

        double Total = CalcConvexArea(p,n);

        int tot = 0, fir = 0, add = 0;

        ch[tot++] = p[0];

        for(i=0;i<n;i++)

        {

            Point C = p[i], D = p[(i+1)%n];

            if(SegmentIntersection(A,B,C,D))

            {

                SegIntersectionPoint(P,A,B,C,D);

                ch[tot++] = P;

                if(!fir) fir = 1;

                else     fir = 0, add = 1;

                if(P == D) i++;

            }

            else if(!fir) ch[tot++] = p[(i+1)%n];

            if(add) ch[tot++] = p[(i+1)%n];

        }

        double Now = CalcConvexArea(ch,tot);

        double Other = Total-Now;

        int N = (int)(Now+0.5), O = (int)(Other+0.5);

        if(O > N) swap(N,O);

        printf("%d %d\n",N,O);

    }

    return 0;

}

View Code