Bottom-Up Parsing
4.5 Bottom-Up Parsing
A bottom-up parse corresponds to the construction of a parse tree for an input string beginning at the leaves (the bottom) and working up towards the root (the top). It is convenient to describe parsing as the process of building parse trees, although a front end may in fact carry out a translation directly without building an explicit tree. The sequence of tree snapshots in Fig. 4.25 illustrates a bottom-up parse of the token stream id * id, with respect to the expression grammar (4.1).

Figure 4.25: A bottom-up parse for id * id
This section introduces a general style of bottom-up parsing known as shiftreduce parsing. The largest class of grammars for which shift-reduce parsers can be built, the LR grammars, will be discussed in Sections 4.6 and 4.7. Although it is too much work to build an LR parser by hand, tools called automatic parser generators make it easy to construct efficient LR parsers from suitable grammars. The concepts in this section are helpful for writing suitable grammars to make effective use of an LR parset generator. Algorithms for implementing patser generators appear in Section 4.7.
4.5.1 Reductions
We can think of bottom-up parsing as the process of "reducing" a string ω to the start symbol of the grammar. At each reduction step, a specific substring matching the body of a production is replaced by the nonterminal at the head of that production.
The key decisions during bottom-up parsing are about when to reduce and about what production to apply, as the parse proceeds.
Example 4.37: The snapshots in Fig. 4.25 illustrate a sequence of reductions; the grammar is the expression grammar (4.1). The reductions will be discussed in terms of the sequence of strings
id * id, F * id, T * id, T * F, T, EThe strings in this sequence are formed from the roots of all the subtrees in the snapshots. The sequence starts with the input string id * id. The first reduction produces F * id by reducing the leftmost id to F, using the production F -> id. The second reduction produces T * id by reducing F to T.
Now, we have a choice between reducing the string T, which is the body of E -> T, and the string consisting of the second id, which is the body of F -> id. Rather than reduce T to E, the second id is reduced to T, resulting in the string T * F. This string then reduces to T. The parse completes with the reduction of T to the start symbol E. □
By definition, a reduction is the reverse of a step in a derivation (recall that in a derivation, a nonterminal in a sentential form is replaced by the body of one of its productions). The goal of bottom-up parsing is therefore to construct a derivation in reverse. The following derivation corresponds to the parse in Fig. 4.25:
E => T => T * F => T * id => F * id => id * id
This derivation is in fact a rightmost derivation.
4.5.2 Handle Pruning
Bottom-up parsing during a left-to-right scan of the input constructs a rightmost derivation in reverse. Informally, a "handle" is a substring that matches the body of a production, and whose reduction represents one step along the reverse of a rightmost derivation.
For example, adding subscripts to the tokens id for clarity, the handles during the parse of id1 * id2 according to the expression grammar (4.1) are as in Fig. 4.26. Although T is the body of the production E -> T, the symbol T is not a handle in the sentential form T * id2. If T were indeed replaced by E, we would get the string E * id2, which cannot be derived from the start symbol E. Thus, the leftmost substring that matches the body of some production need not be a handle.
| RIGHT SENTENTIAL FORM | HANDLE | REDUCING PRODUCTION |
id1 * id2 |
id1 |
F->id |
| F * id2 | F | T->F |
| T* id2 | id2 | F->id |
| T * F | T * F | E->T * F |
Figure 4.26: Handles during a parse of id1 * id2
Formally, if S => αAω => αβω, as in Fig. 4.27, then production A -> β in the position following α is a handle of αβω. Alternatively, a handle of a right-sentential form γ is a production A -> β and a position of γ where the string β may be found, such that replacing β at that position by A produces the previous right-sentential form in a rightmost derivation of γ.

Figure 4.27: A handle A -> β in the parse tree for αβω
Notice that the string ω to the right of the handle must contain only terminal symbols. For convenience, we refer to the body β rather than A -> β as a handle. Note we say "a handle" rather than "the handle", because the grammar could be ambiguous, with more than one rightmost derivation of αβω. If a grammar is unambiguous, then every right-sentential form of the grammar has exactly one handle.
A rightmost derivation in reverse can be obtained by "handle pruning". That is, we start with a string of terminals ω to be parsed. If ω is a sentence of the grammar at hand, then let ω = γn, where γn is the nth right-sentential form of some as yet unknown rightmost derivation
S => γ 1 => γ 2 => … => γ n = ω
To reconstruct this derivation in reverse order, we locate the handle βn in "in and replace βn by the head of the relevant production An -> βn to obtain the previous right-sentential form γn-1. Note that we do not yet know how handles are to be found, but we shall see methods of doing so shortly.
We then repeat this process. That is, we locate the handle βn-1 in γn-1 and reduce this handle to obtain the right-sentential form γn-2 . If by continuing this process we produce a right-sentential form consisting only of the start symbol S, then we halt and announce successful completion of parsing. The reverse of the sequence of productions used in the reductions is a rightmost derivation for the input string.
4.5.3 Shift-Reduce Parsing
Shift-reduce parsing is a form of bottom-up parsing in which a stack holds grammar symbols and an input buffer holds the rest of the string to be parsed. As we shall see, the handle always appears at the top of the stack just before it is identified as the handle.
We use $ to mark the bottom of the stack and also the right end of the input. Conventionally, when discussing bottom-up parsing, we show the top of the stack on the right, rather than on the left as we did for top-down parsing. Initially, the stack is empty, and the string ω is on the input, as follows:
| STACK | INPUT |
| $ | ω$ |
During a left-to-right scan of the input string, the parser shifts zero or more input symbols onto the stack, until it is ready to reduce a string β of grammar symbols on top of the stack. It then reduces β to the head of the appropriate production. The parser repeats this cycle until it has detected an error or until the stack contains the start symbol and the input is empty:
| STACK | INPUT |
| $S | $ |
Upon entering this configuration, the parser halts and announces successful completion of parsing. Figure 4.28 steps through the actions a shift-reduce parser might take in parsing the input string id1 *id2 according to the expression grammar (4.1).
| STACK | INPUT | ACTION |
| $ | id1 * id2 $ | shift |
| $ id1 | * id2 $ | reduce by F->id |
| $ F | * id2 $ | reduce by T->F |
| $ T | * id2 $ | shift |
| $ T * | id2 $ | shift |
| $ T * id2 | $ | reduce by F –>id |
| $ T * F | $ | reduce by T –> T * F |
| $ T | $ | reduce by E –> T |
| $ E | $ | accept |
Figure 4.28: Configurations of a shift-reduce parser on input id1 *id2
While the primary operations are shift and reduce, there are actually four possible actions a shift-reduce parser can make: (1) shift, (2) reduce, (3) accept, and (4) error.
- Shift. Shift the next input symbol onto the top of the stack.
- Reduce. The right end of the string to be reduced must be at the top of the stack. Locate the left end of the string within the stack and decide with what nonterminal to replace the string.
- Accept. Announce successful completion of parsing.
- Error. Discover a syntax error and call an error recovery routine.
The use of a stack in shift-reduce parsing is justified by an important fact: the handle will always eventually appear on top of the stack, never inside. This fact can be shown by considering the possible forms of two successive steps in any rightmost derivation. Figure 4.29 illustrates the two possible cases. In case (1), A is replaced by β By , and then the rightmost nonterminal B in the body β By is replaced by γ. In case (2), A is again expanded first , but this time the body is a string y of terminals only. The next rightmost nonterminal B will be somewhere to the left of y.
In other words:
- S => αAz => αβByz => αβγyz
- S => αBxAz => αBxyz => αγxyz
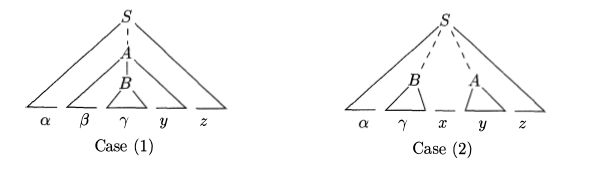
Figure 4.29: Cases for two successive steps of a rightmost derivation
Consider case (1) in reverse, where a shift-reduce parser has just reached the configuration
| STACK | INPUT |
| $αβγ | yz$ |
The parser reduces the handle γ to B to reach the configuration
| STACK | INPUT |
| $αβB | yz$ |
The parser can now shift the string y onto the stack by a sequence of zero or more shift moves to reach the configuration
| $αβBy | z$ |
with the handle βBy on top of the stack, and it gets reduced to A.
Now consider case (2). In configuration
| $αγ | xyz$ |
the handle γ is on top of the stack. After reducing the handle γ to B, the parser can shift the string xy to get the next handle y on top of the stack, ready to be reduced to A:
| $αBxy | z$ |
In both cases, after making a reduction the parser had to shift zero or more symbols to get the next handle onto the stack. It never had to go into the stack to find the handle.
4.5.4 Conflicts During Shift-Reduce Parsing
There are context-free grammars for which shift-reduce parsing cannot be used. Every shift-reduce parser for such a grammar can reach a configuration in which the parser, knowing the entire stack contents and the next input symbol, cannot decide whether to shift or to reduce (a shift/reduce conflict), or cannot decide which of several reductions to make (a reduce/reduce conflict). We now give some examples of syntactic constructs that give rise to such grammars. Technically, these grammars are not in the LR(k) class of grammars defined in Section 4.7; we refer to them as non-LR grammars. The k in LR(k) refers to the number of symbols of lookahead on the input. Grammars used in compiling usually fall in the LR(1) class, with one symbol of lookahead at most.
Example 4.38: An ambiguous grammar can never be LR. For example, consider the dangling-else grammar (4.14) of Section 4.3:
stmt : if expr then stmt
| if expr then stmt else stmt
| other
If we have a shift-reduce parser in configuration
| STACK | INPUT |
| … if expr then stmt | else … $ |
we cannot tell whether if expr then stmt is the handle, no matter what appears below it on the stack. Here there is a shift/reduce conflict. Depending on what follows the else on the input, it might be correct to reduce if expr then stmt to stmt, or it might be correct to shift else and then to look for another stmt to complete the alternative if expr then stmt else stmt.
Note that shift-reduce parsing can be adapted to parse certain ambiguous grammars, such as the if-then-else grammar above. If we resolve the shift/reduce conflict on else in favor of shifting, the parser will behave as we expect, associating each else with the previous unmatched then. We discuss parsers for such ambiguous grammars in Section 4.8.□
Another common setting for conflicts occurs when we know we have a handle, but the stack contents and the next input symbol are insufficient to determirie which production should be used in a reduction. The next example illustrates this situation.
Example 4.39: Suppose we have a lexical analyzer that returns the token name id for all names, regardless of their type. Suppose also that our language invokes procedures by giving their names, with parameters surrounded by parentheses, and that arrays are referenced by the same syntax. Since the translation of indices in array references and parameters in procedure calls are different, we want to use different productions to generate lists of actual parameters and indices. Our grammar might therefore have (among others) productions such as those in Fig. 4.30.
| 1 | stmt | -> | id(parameter_list) |
| 2 | stmt | -> | expr:=expr |
| 3 | parameter_list | -> | parameter_list,parameter |
| 4 | parameter_list | -> | parameter |
| 5 | parameter | -> | id |
| 6 | expr | -> | id(expr_list) |
| 7 | expr | -> | id |
| 8 | expr_list | -> | expr_list,expr |
| 9 | expr_list | -> | expr |
Figure 4.30: Productions involving procedure calls and array references
A statement beginning with p(i, j) would appear as the token stream id(id, id) to the parser. After shifting the first three tokens onto the stack, a shift-reduce parser would be in configuration
| STACK | INPUT |
| … id ( id | , id ) … |
It is evident that the id on top of the stack must be reduced, but by which production? The correct choice is production (5) if P is a procedure, but production (7) if p is an array. The stack does not tell which; information in the symbol table obtained from the declaration of p must be used.
One solution is to change the token id in production (1) to procid and to use a more sophisticated lexical analyzer that returns the token name procid when it recognizes a lexeme that is the name of a procedure. Doing so would require the lexical analyzer to consult the symbol table before returning a token.
If we made this modification, then on processing p(i, j) the parser would be either in the configuration
| STACK | INPUT |
| … procid ( id | , id ) … |
or in the configuration above. In the former case, we choose reduction by production (5); in the latter case by production (7). Notice how the symbol third from the top of the stack determines the reduction to be made, even though it is not involved in the reduction. Shift-reduce parsing can utilize information far down in the stack to guide the parse.□