二重积分换元法的一种简单证明
10.3二重积分的换元积分法
在一元函数定积分的计算中,我们常常进行换元,以达删繁就简的目的,当然,二重积分也有换元积分的问题。
首先让我们回顾一下前面曾讨论的一个事实。
设换元函数 ![]() ,视其为一个由定义域
,视其为一个由定义域![]() 到
到![]() 的映射.点
的映射.点![]() 的象点为
的象点为![]() ,点x的象点为
,点x的象点为![]() ,记
,记
![]() ,
,
则由![]() 到点
到点![]() 的线段长为
的线段长为![]() ,
,![]() 到
到![]() 的线段长为
的线段长为![]() ,称
,称![]() 为映射
为映射![]() 在点
在点![]() 到点
到点![]() 的平均伸缩率。若
的平均伸缩率。若![]() 在点
在点![]() 处可导,则
处可导,则
![]()
![]() =
=![]()

即![]() 称
称![]() 是映射
是映射![]() 在点
在点![]() 处的伸缩率。
处的伸缩率。
对于由平面区域![]() 到
到![]() 的映射
的映射 我们有如下结论:
我们有如下结论:
引理 若变换![]() 在开区域
在开区域![]() 存在连续偏导数,且雅可比行列式
存在连续偏导数,且雅可比行列式![]() ,
,![]() 。变换将
。变换将![]() 平面上开区域变为
平面上开区域变为![]() 平面上开区域
平面上开区域![]() 。
。![]()
![]() ,其象点为
,其象点为![]()
![]()
![]()
![]() ,则包含点
,则包含点![]() 的面积微元
的面积微元![]() 及与之相对应的包含点
及与之相对应的包含点![]() 的面积微元
的面积微元![]() 之比是
之比是 ,即
,即![]() =
=
![]()
下面给出引理3.1的说明,严格的证明从略。由图3。1所示,在![]() 内作以点
内作以点![]() 为顶点的矩形
为顶点的矩形![]() ,而变换
,而变换![]() ,将
,将![]() 分别变为
分别变为![]() 平面上的四点
平面上的四点![]() ,矩形
,矩形![]() 变为曲边四边形
变为曲边四边形![]() 。而曲边四边形
。而曲边四边形![]() 的四个顶点的坐标由泰勒公式表示为
的四个顶点的坐标由泰勒公式表示为![]() :
:![]()
![]() :
:![]()
![]()

![]()
![]()
![]() :
:![]()
![]() +
+![]()
![]()
![]() +
+![]()
![]() :
:![]()
![]()
![]()
![]()
忽略高阶无穷小![]() 与
与![]() ,曲边四边形
,曲边四边形![]() 近似平行四边形,其面积
近似平行四边形,其面积
 =
= =
=
![]() =
= 其中
其中![]() 是矩形
是矩形![]() 的面积。于是
的面积。于是

在引理条件下,函数组![]() ,在
,在![]() 的某邻域
的某邻域![]() 具有连续的反函数组
具有连续的反函数组![]()
![]()
再根据9.1节性质1.2有 =
= 于是
于是![]() =
=
![]() =
=
![]()
定理3.1 若函数![]() 在有界闭区域
在有界闭区域![]() 连续,函数组将
连续,函数组将![]() 平面上区域
平面上区域![]() 一一对应地变换为
一一对应地变换为![]() 平面上区域
平面上区域![]() ,且该函数组在
,且该函数组在![]() 存在连续的偏导数,,则
存在连续的偏导数,,则
![]() =
=![]()

![]()
证 用任意分法![]() 将区域
将区域![]() 分成
分成![]() 个小区域
个小区域![]() ,其面积分别记为
,其面积分别记为![]() ;变换
;变换![]() ,将分法
,将分法![]() 变为
变为![]() 上的分法
上的分法![]() ,
,![]() 将
将![]() 分割成
分割成![]() 个小区域
个小区域![]() ,其面积分别记为
,其面积分别记为![]() ,由引理可知,对于
,由引理可知,对于![]()
![]() ,有
,有
![]()
![]()

![]() 于是
于是![]() ,在
,在![]() 上对应唯一点
上对应唯一点![]() 且
且![]()
![]()
![]()
![]() ,于是
,于是![]()
![]()
![]()
![]()

![]()
在定理3.2的条件下,变换![]() 在有界闭区域
在有界闭区域![]() 上存在连续的反函数组
上存在连续的反函数组![]() ,他们必在
,他们必在![]() 上一致连续,所以当
上一致连续,所以当![]() 时,必有又注意到函数
时,必有又注意到函数![]()
 在
在![]() 的连续性,因而他在
的连续性,因而他在![]() 上可积,于是在
上可积,于是在![]() 中令
中令![]() ,有
,有![]() =
=![]()

![]() 完成定理3。2的证明。
完成定理3。2的证明。
在二重积分的计算中,若被积函数为![]() 的形式,或积分区域为所谓的圆形区域时,通常采用极坐标变换
的形式,或积分区域为所谓的圆形区域时,通常采用极坐标变换![]() 它能使前者化简为一元函数
它能使前者化简为一元函数![]() 。
。

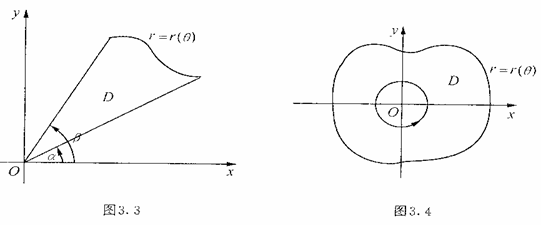
后者若为图3.2所示的区域,利用极坐标变换能化为![]() 平面上的
平面上的![]() 型区域。则积分
型区域。则积分![]() =
=![]()

![]() =
=![]()
![]()
![]()
=![]()
特别,极点在边界上的扇形区域,即![]() ,则积分
,则积分
![]() =
=![]()
极点在区域![]() 的内部,边界线是
的内部,边界线是![]() 的区域,即
的区域,即![]() 则积分
则积分
![]() =
=![]()
![]()
![]()
![]() 例3.1 计算
例3.1 计算![]()
![]() 解 作极坐标变换
解 作极坐标变换 ![]() 将圆域D变换为矩形区域,
将圆域D变换为矩形区域,
![]()
![]() ,于是用公式(3.5)得
,于是用公式(3.5)得
![]()
![]() =
=![]()
![]()
![]() 例3.2 计算
例3.2 计算![]()
![]() ,D是由
,D是由
![]() 和
和![]() 所围的区域。
所围的区域。
解 积分区域如图3.5所示,作极坐标变换,则D化为区域![]() ,其边界曲线为
,其边界曲线为![]() =
=![]() ,
,![]() ,于是得
,于是得
![]() =
=![]() =
=![]()
例3.3 ![]() 其中D是由
其中D是由![]() 所围成的平面区域
所围成的平面区域

解 区域D及![]() 如图3.6所示,有
如图3.6所示,有![]() =
=![]() -
-![]() 而
而![]() =4
=4
在极坐标系下,有![]() , 因此
, 因此![]() =
=![]() 于是
于是![]() =4-
=4-![]() .
.
例3.4 计算![]() ,其中D是由曲线
,其中D是由曲线![]() 所围成的有界区域.
所围成的有界区域.
解由于积分区域D可表示为 故替换
故替换
 ,则积分区域变为
,则积分区域变为 ,在极坐标下
,在极坐标下
![]()
于是

例3.5 计算![]()
解 由对称性,原积分
![]()
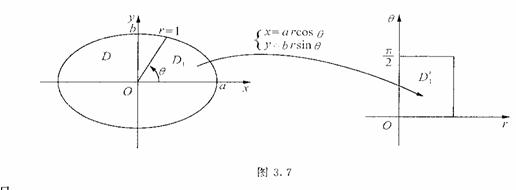
其中 。作广义极坐标变换:
。作广义极坐标变换:![]()
则![]() 变换为矩形区域
变换为矩形区域![]() (图3.7)
(图3.7)
且
![]()
于是
![]()
![]()
![]()
例3.6 求曲线![]() 与
与![]() 所围成区域
所围成区域![]() 的面积
的面积
解由二重积分的性质可知,区域的面积
![]()
作变换:
![]() ,
,
则这个变换![]() 平面上曲线
平面上曲线![]() 变为
变为![]() 平面
平面
上的曲线![]() 、
、![]() 变为
变为![]() ,于是它将区域
,于是它将区域![]() 变为
变为
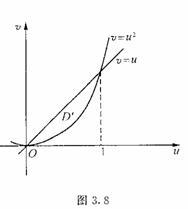
![]() 平面上由
平面上由![]() 和
和![]() 所未成的区域
所未成的区域![]() (图3.8 )。且
(图3.8 )。且

于是![]()
![]()
例3.7 计算![]()
解 作变换:![]() 则
则![]() ,将
,将![]() 变换为闭圆域
变换为闭圆域![]() ,且
,且
![]()
故![]()
由对称性
![]()
于是![]()
例3.8 计算![]() ,
,![]() 是由
是由![]() 、
、![]() 、
、![]() 和
和![]() 所围成的区域。
所围成的区域。
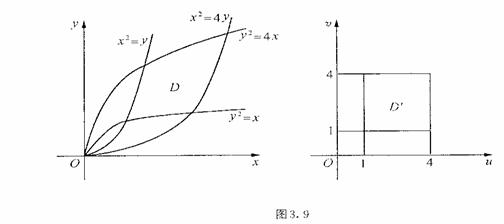
解 作变换:![]() ,
,![]() ,则这个变换将
,则这个变换将![]() 变换为
变换为![]() 平面上的正方形区域(图3.9)。由于
平面上的正方形区域(图3.9)。由于

且

故 ![]()
又注意到![]() ,于是
,于是
![]()
![]()