poj 1330 Nearest Common Ancestors LCA

题目链接：http://poj.org/problem?id=1330

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below: 

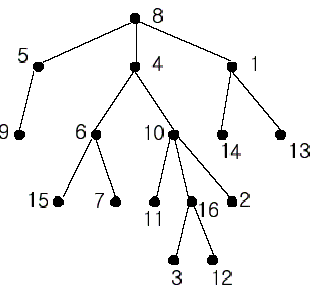
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is. 

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.

Write a program that finds the nearest common ancestor of two distinct nodes in a tree. 

题意描述：在一个DAG中，定义节点u是节点v的祖先：节点u是树根到节点v的路径上的一个节点。 给出一些节点之间的关系，求出两个节点的最近公共祖先。

算法分析：最近公共祖先（LCA）的入门题。

最近公共祖先算法的大致思路：

1：求出每个节点的2^k（0<=k<max_log_n）的祖先节点。节点u的2^0（第一代）祖先节点就是u的父亲节点，那么我们可以得到u的第一代、第二代、第四代、第八代...祖先节点。

2：把节点u和v深度大的节点根据1中的算法思想移到和深度小的节点同一深度（树根深度为0，树根的儿子节点深度为1），然后再一起往上移，即可求出LCA。

 1 #include<iostream>

 2 #include<cstdio>

 3 #include<cstring>

 4 #include<cstdlib>

 5 #include<cmath>

 6 #include<algorithm>

 7 #include<vector>

 8 #define inf 0x7fffffff

 9 using namespace std;

10 const int maxn=10000+10;

11 const int max_log_maxn=14;

12 

13 int n,A,B,root;

14 vector<int> G[maxn];

15 int father[max_log_maxn][maxn],d[maxn];

16 

17 void dfs(int u,int p,int depth)

18 {

19     father[0][u]=p;

20     d[u]=depth;

21     int num=G[u].size();

22     for (int i=0 ;i<num ;i++)

23     {

24         int v=G[u][i];

25         if (v != father[0][u]) dfs(v,u,depth+1);

26     }

27 }

28 

29 void init()

30 {

31     dfs(root,-1,0);

32     for (int k=0 ;k+1<max_log_maxn ;k++)

33     {

34         for (int i=1 ;i<=n ;i++)

35         {

36             if (father[k][i]<0) father[k+1][i]=-1;

37             else father[k+1][i]=father[k][father[k][i] ];

38         }

39     }

40 }

41 

42 int LCA()

43 {

44     if (d[A]<d[B]) swap(A,B);

45     for (int k=0 ;k<max_log_maxn ;k++)

46     {

47         if ((d[A]-d[B])>>k & 1)

48         {

49             A=father[k][A];

50         }

51     }

52     if (A==B) return A;

53     for (int k=max_log_maxn-1 ;k>=0 ;k--)

54     {

55         if (father[k][A] != father[k][B])

56         {

57             A=father[k][A];

58             B=father[k][B];

59         }

60     }

61     return father[0][A];

62 }

63 

64 int main()

65 {

66     int t;

67     scanf("%d",&t);

68     while (t--)

69     {

70         scanf("%d",&n);

71         for (int i=0 ;i<=n ;i++) G[i].clear();

72         for (int i=0 ;i<max_log_maxn ;i++)

73         {

74             for (int j=0 ;j<maxn ;j++)

75                 father[i][j]=-1;

76         }

77         int a,b;

78         int vis[maxn];

79         memset(vis,0,sizeof(vis));

80         for (int i=0 ;i<n-1 ;i++)

81         {

82             scanf("%d%d",&a,&b);

83             G[a].push_back(b);

84             vis[b]=1;

85         }

86         scanf("%d%d",&A,&B);

87         for (int i=1 ;i<=n ;i++) if (!vis[i]) {root=i;break; }

88         init();

89         printf("%d\n",LCA());

90     }

91     return 0;

92 }