Recurrent Neural Network(循环神经网络)

Reference:   Alex Graves的[Supervised Sequence Labelling with RecurrentNeural Networks]

Alex是RNN最著名变种，LSTM发明者Jürgen Schmidhuber的高徒，现加入University of Toronto，拜师Hinton。

统计语言模型与序列学习

1.1 基于频数统计的语言模型

NLP领域最著名的语言模型莫过于N-Gram。

它基于马尔可夫假设，当然，这是一个2-Gram(Bi-Gram)模型：

任意一个词$W_{i}$出现的概率只同它前面的词$W_{i-1}$有关。

迁移到N-Gram中，就变成：

在一个句子当中，一个单词的T出现的概率，和其前N个单词是有关的:

$P(W_{t}|W_{t-N}....,W_{t-1},W_{t+1}....,W_{t+N})$

早期计算Bi-Gram的方法，正如吴军博士所著的《数学之美》里科普的那样，采用词频统计法：

$P(W_{i}|W_{i-1})=\frac{P(W_{i-1},W_{i})}{P(W_{i-1})}\approx \frac{Cnt(W_{i-1},W_{i})}{Cnt(W_{i-1})}$

只需要统计一下$W_{i}$、$W_{i-1}$一起出现的频数就可以了。

看起来确实很简单，很数学之美。当然，作为一本科普读物，它是不会告诉你这种方法是有多大危害的。

具体实现，可以使用以下两个算法：

①KMP：将$W_{i}$、$W_{i-1}$两个词拼在一起，跑一次Text串。

②AC自动机：同样拼接，不过是预先拼好所有的模式串，输入AC自动机里，仅仅跑一次Text串。

但如果你是一名ACM选手，应该对AC自动机深有体会，这玩意简直就是内存杀手。

两者相害，取其轻。很明显，实际运用的时候，根本不会考虑KMP，优先选择空间换时间的AC自动机算法。

在[CS224D Lecture7]中，Socher提到了N-Gram频数统计法的state-of-art结果，[Heafield 2013]

看看Abstract就够吓人了：

Using one machine with 140 GB RAM for 2.8 days, we built an unpruned model on 126 billion tokens.

还是建立在 MapReduce 上。这种吃硬件的方法，不得不说，真是够糟糕的。

1.2 基于神经网络的语言模型

Neural Network Language Model (NNLM)，最早正式在[Bengio03]提出。

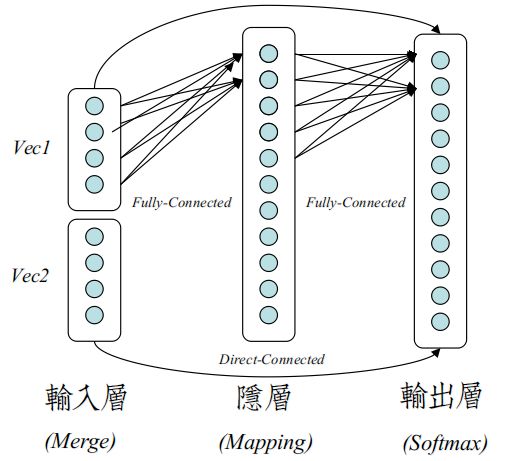
Bengio使用的是一个经典的前馈网络来训练N-Gram不同之处在于，输入层是可训练的。

输入层最后被训练成Word Vector，在[Mikolov13]提出Word2Vec之前，大多称为Word Embeddings。

具体的方法:

①为每个词，构建$|N*Dim|$的向量参数。这点与Word2Vec的简化方法有所不同。

Word2Vec取消训练了词序信息，所以向量大小是$|Dim|$。

②拿到一个句子，句子长度是T，利用词的索引，组合出$|T，N*Dim|$的输入矩阵。

③如普通NN一样，Softmax误差，BP传播，更新。

NNLM方法，轻量的复现的N-Gram模型，需要更少的内存。且无须做平滑处理，如[Katz backoff]。

1.3 序列学习

正如朴素贝叶斯假设一样，马尔可夫假设也是一种糟糕的近似。

对于一个词$W_{i}$，只覆盖前N个词，很多时候是抓不住重点的。

最好的解决方案，当然是对于一个词$W_{i}$，覆盖其前面的所有词。

模仿动态规划原理，构建成一个动态序列模型。这需要Recurrent Neural Network(RNN)来实现。

RNN通常译为循环神经网络，其类似动态规划的原理，也可译为时序递归神经网络。

当然还有结构递归神经网络RNN（Recursive Neural Network)，使用频率不高，没落。

通常RNN指的是时序递归RNN。

 

RNN结构与更新

2.1 经典之作：Elman's Simple Recurrent Networks(SRN)

J. L. Elman提出的SRN是RNN系中结构最简单的一个变种，相较于传统的2层FC前馈网络，它仅仅在FC层添加了时序反馈连接。

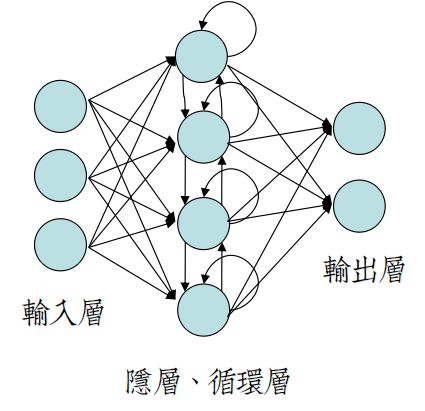
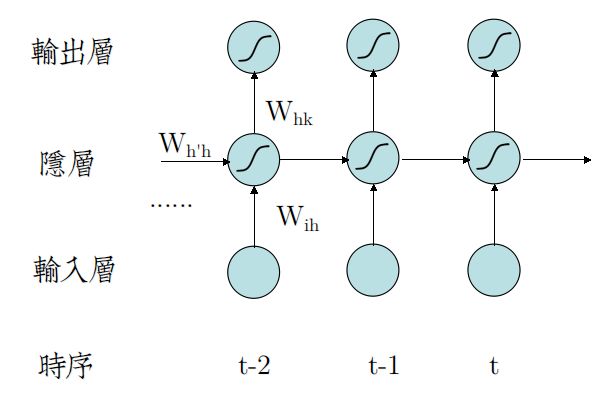
左图是不完整的结构图，因为循环层的环太难画，包含自环、交叉环。

所以RNN一般都画成时序展开图，如右图。

从时序展开图中，容易看出，SRN在时序t时，前面的全部状态，压缩在一起，输入到当前隐层中。

因而，RNN可以看成是具有动态深度结构的图模型，随着时序的增加，网络深度越来越大，因而属于深度神经网络。

2.2 前向传播

较于2层前馈网络，唯一变化是，时序为$t$时，隐层输入由两部分组成：

①输入层映射变换。(非递归)

②时序为$t-1$时，隐层神经元的激活输出。(时序递归)

以下用$a_{j}^{t}$表示神经元j的输入，$b_{j}^{t}$表示神经元j的激活后输出，为表示清晰，忽略Bias。

输入到达隐层时，有：

$a_{h}^{t}=\sum_{i=1}^{I}w_{ih}x_{i}^{t}+\sum_{h^{'}=1}^{H}w_{h^{'}h}b_{h^{'}}^{t-1}$

多出的$h^{'}->h$变换，大可称为隐隐层变换，为前馈网络带来记忆槽。

它记忆着时序$[1,t-1]$到达输出层之前的神经元的全部状态。

激活隐层神经元后，有：

$b_{h}^{t}=Activation(a_{h}^{t})$

经过输出层后，有:

$y_{k}^{t}=Softmax(W_{hk}b_{h}^{t})$

2.3 反向传播

仿照BP网络一样，定义局部梯度：

$\delta _{y}^{t}=\frac{\partial \mathcal{L}}{\partial b_{y}^{t}} \cdot \frac{\partial b_{y}^{t}}{\partial a_{y}^{t}}$

也就是说，从似然函数开始，由链式尾，导到$\partial W$的前一步。

对输出层，有:

$\frac{\partial \mathcal{L}}{\partial W_{hk}}=\delta_{k}^{t}\cdot\frac{\partial a_{j}^{t}}{\partial W_{hk}}$

$\delta_{k}^{t}$即，Softmax里的 $(1\{y_{i}=j\}-P(y^{(i)}=j|x;\theta_{j})),j=1,2....k$

对隐隐层，有:

$\frac{\partial \mathcal{L}}{\partial W_{h^{'}h}}=\sum_{p=1}^{t}\frac{\partial \mathcal{L}}{\partial b_{k}^{t}}\cdot\frac{\partial b_{k}^{t}}{\partial a_{k}^{t}}\cdot\frac{\partial b_{h}^{t}}{\partial b_{h}^{p}}\cdot\frac{\partial b_{h}^{p}}{\partial W_{h^{'}h}} \qquad where \quad  \frac{\partial b_{h}^{t}}{\partial b_{h}^{p}}=\prod_{j=p+1}^{t}\frac{\partial b_{h}^{j}}{\partial b_{h}^{j-1}}$

上式来自[CS224d Lecture7]，是RNN的Feet of Clay，需要牢记。

因为需要累乘，相当于求一个超深度神经网络结构的梯度，会带来严重的Gradient Vanish\Exploding。下文会详细描述。

至于为什么可以写成那样，你可以用一个简单的单神经元，无激活函数的网络推一下：

$a_{3}=wx_{3}+w^{'}a_{2}=....=wx_{3}+w^{'}wx_{2}+(w^{'})^{2}wx_{1}\\\\\frac{\partial a_{3}}{w^{'}}=????\\\\Answer=\frac{\partial a_{3}}{\partial a_{3}}\cdot\frac{\partial a_{3}}{w^{'}}+\frac{\partial a_{3}}{\partial a_{3}}\cdot\frac{\partial a_{3}}{\partial a_{2}}\cdot\frac{\partial a_{2}}{w^{'}}+\frac{\partial a_{3}}{\partial a_{3}}\cdot\frac{\partial a_{3}}{\partial a_{2}}\cdot\frac{\partial a_{2}}{\partial a_{1}}\cdot\frac{\partial a_{1}}{w^{'}}$

同样，去掉后面的部分，有局部梯度：

$\delta_{h^{'}}^{t}=\sum_{p=1}^{t}\frac{\partial \mathcal{L}}{\partial b_{k}^{t}}\cdot\frac{\partial b_{k}^{t}}{\partial a_{k}^{t}}\cdot\frac{\partial b_{h}^{t}}{\partial b_{h}^{p}} \qquad where \quad  \frac{\partial b_{h}^{t}}{\partial b_{h}^{p}}=\prod_{j=p+1}^{t}\frac{\partial b_{h}^{j}}{\partial b_{h}^{j-1}}$

这样，对隐层，就有著名的BPTT更新法则，正如[Alex]书中所写：

$\delta _{h}^{t}=Activation^{'}(a_{h}^{t})\begin{pmatrix}\sum_{k=1}^{K}\delta _{k}^{t}w_{hk}+\sum_{h^{'}=1}^{H}\delta _{h^{'}}^{t+1}w_{hh^{'}}\end{pmatrix}$

当然$\delta _{h^{'}}^{T+1}$会越界，等于0。

这里，最头疼的是，为什么隐隐层的局部梯度是取决于时序t+1的？

这个需要跨越一步来看，$W^{t}$不仅会在当前时序t，作为隐层参数出现，还会在时序t+1，作为隐隐层的附加参数出现。

这样，链式法则波及到了时序t，以及时序t+1，所以局部梯度由两部分组成，这是BPTT更新法的精髓。

最后一部分:

$\frac{\partial \mathcal{L}}{\partial W_{ih}}=\frac{\partial \mathcal{L}}{\partial a_{h}^{t}}\cdot\frac{\partial a_{h}^{t}}{\partial W_{ih}}=\delta _{h}^{t}x_{i}^{t}$