EOJ Monthly 2020.7

A - 打字机 （思维）

显然如果使用第二种构造,$a$和$b$是成对出现的，如果$a$的数目较多就必须再使用第一种构造，因此：

• $a$的数目和$b$的数目相同且$a$均在$b$的前面；或者只有$a$，就是$happy$
• $b$的数目大于$a$的数目是$dead$
• 否则为$sad$

#include <set>
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <cstdio>
#include <string>
#include <bitset>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define ins insert
#define Vector Point
#define lowbit(x) (x&(-x))
#define mkp(x,y) make_pair(x,y)
#define mem(a,x) memset(a,x,sizeof a);
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<double,double> pdd;
const double eps=1e-8;
const double pi=acos(-1.0);
const int inf=0x3f3f3f3f;
const double dinf=1e300;
const ll INF=1e18;
const int Mod=1e9+7;
const int maxn=2e5+10;

string s;

int main(){
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        s="";
        cin>>s;
        int A=0,B=0,flag=2;
        for(auto i: s){
            if(i=='a'){
                A++;
            }else{
                B++;
                if(A==B){
                    flag=2;
                }else if(A>B){
                    flag=1;
                }else{
                    flag=0;
                    goto done;
                }

            }
        }
        done:
            if(!flag) cout<<"Dead Fang"<<endl;
            else if(flag==1) cout<<"Sad Fang"<<endl;
            else cout<<"Happy Fang"<<endl;
    }
    return 0;
}

B - 线上考试（签到）

#include <set>
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <cstdio>
#include <string>
#include <bitset>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define ins insert
#define Vector Point
#define lowbit(x) (x&(-x))
#define mkp(x,y) make_pair(x,y)
#define mem(a,x) memset(a,x,sizeof a);
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<double,double> pdd;
const double eps=1e-8;
const double pi=acos(-1.0);
const int inf=0x3f3f3f3f;
const double dinf=1e300;
const ll INF=1e18;
const int Mod=1e9+7;
const int maxn=2e5+10;

ll qkp(ll x,ll n){
    ll ans=1;
    while(n){
        if(n&1) ans*=x;
        x*=x;
        n>>=1;
    }
    return ans;
}

int main(){
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int n;
    ll x;
    char c;
    cin>>n;
    ll res=0;
    while(n--){
        cin>>c>>x;
        if(c=='S') res=max(res,x);
        else{
            res=max(res,qkp(2,x)-1);
        }
    }
    cout<<res<<endl;
    return 0;
}

C. OLED（二维前缀和）

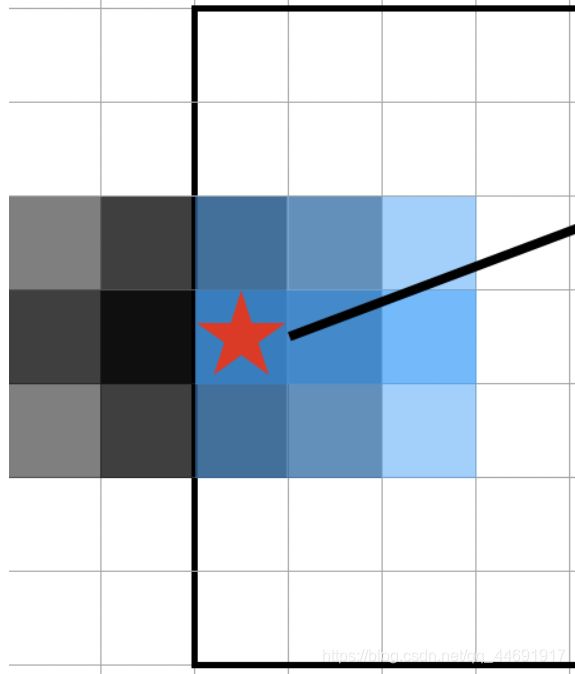
实际上某一块被覆盖的次数和它的上下左右边界是有关的，当然这四个边界都不能超过屏保区域的边界，那么我们预处理屏保的二维前缀和，然后求出每一块的四个边界，注意细节，画个图举一个边界的例子即可明白，通过边界即可求出对应屏保区域的和

如下图是在某个边界，屏保的区域为$2\times 3$

#include <set>
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <cstdio>
#include <string>
#include <bitset>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define ins insert
#define Vector Point
#define lowbit(x) (x&(-x))
#define mkp(x,y) make_pair(x,y)
#define mem(a,x) memset(a,x,sizeof a);
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<double,double> pdd;
const double eps=1e-8;
const double pi=acos(-1.0);
const int inf=0x3f3f3f3f;
const double dinf=1e300;
const ll INF=1e18;
const int Mod=1e9+7;
const int maxn=2e5+10;

int ans[4000][2500],sum[4000][2500];
int n,m,a,b,x;

int main(){
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m>>a>>b;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            cin>>x;
            sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+x;
        }
    int Max=0;
    for(int i=1;i<=a;i++)
        for(int j=1;j<=b;j++){
            int l=j,r=b-j+1,u=i,d=a-i+1;
            int x1,x2,y1,y2;
            if(d>=n) x1=1;
            else x1=n-d+1;
            if(r>=m) y1=1;
            else y1=m-r+1;
            x2=min(n,u);
            y2=min(m,l);
            ans[i][j]=sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1];
            Max=max(Max,ans[i][j]);
        }
    for(int i=1;i<=a;i++){
        for(int j=1;j<=b;j++)
            cout<<int(((double)ans[i][j]/Max)*100)<<' ';
        cout<<"\n";
    }
    return 0;
}

D - 前缀排序

留坑

E - 因数串（思维+构造）

按照样例给的规律，首先肯定从1开始，先从第一个质因数增大到最大次幂，然后乘第二个质因数后慢慢将第一个质因数减小到0次幂，接着将第二个质因数增大到最大次幂，然后乘第一个质因数直到所有因数被构造完毕

题解给的思路是利用进制编码的方式按每个质因子出现的次数编码，最后求答案时类似格雷码的构造——连续两位之间仅有一个位相差为1

第一种方法是很多人写的方法，以例子来分析：（比赛时这个例子折磨我很久也没想出来）

3
2 2
3 2
5 2

• 第一次（初始化）$1,2,2^2$
• 第二次①$[1,2,2^2],[3,2\ast 3,2^2\ast 3]$
• 第二次②$[1,2,2^2],[2^2\ast 3,2\ast 3,3],[3^2,3^2\ast 2,3^2\ast 2^2]$
• 第三次①$[1,2,2^2,2^2\ast 3,2\ast 3,3,3^2,3^2\ast 2,3^2\ast 2^2],[3^2\ast 2^2\ast 5,3^2\ast 2\ast 5,3^2\ast 5,3\ast 5,2\ast 3\ast 5,2^2\ast 3\ast 5,2^2\ast 5,2\ast 5,5]$
• 第三次②$[1,2,2^2,2^2\ast 3,2\ast 3,3,3^2,3^2\ast 2,3^2\ast 2^2],[3^2\ast 2^2\ast 5,3^2\ast 2\ast 5,3^2\ast 5,3\ast 5,2\ast 3\ast 5,2^2\ast 3\ast 5,2^2\ast 5,2\ast 5,5],[5^2,2\ast 5^2,2^2\ast 5^2,2^2\ast 3\ast 5^2,2\ast 3\ast 5^2,3\ast 5^2,3^2\ast 5^2,3^2\ast 2\ast 5^2,3^2\ast 2^2\ast 5^2]$

设加入了某种质因数后的序列为该种序列，我们发现每次对某种质因数的个数遍历，总是在当前序列从后向前取上一种序列长度的数去乘，然后添加到该序列中，相当于是动态维护的过程，因为从前向后每次都乘或除一种质因数，那么从后向前时一定也满足该性质，故此方法正确

#include <set>
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <cstdio>
#include <string>
#include <bitset>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define ins insert
#define Vector Point
#define lowbit(x) (x&(-x))
#define mkp(x,y) make_pair(x,y)
#define mem(a,x) memset(a,x,sizeof a);
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<double,double> pdd;
const double eps=1e-8;
const double pi=acos(-1.0);
const int inf=0x3f3f3f3f;
const double dinf=1e300;
const ll INF=1e18;
const int Mod=1e9+7;
const int maxn=1005;

ll p[maxn],k[maxn];
int fac[10],num[10];
vector<ll> ans;
int n;

int main(){
    ios_base::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>p[i]>>k[i];
    ans.push_back(1);
    ll temp=1;
    for(int i=0;i<k[0];i++) {
        temp*=p[0];
        ans.push_back(temp);
    }
    for(int i=1;i<n;i++){
        int len=ans.size();
        for(int j=0;j<k[i];j++){
            int k=ans.size();
            for(int l=0;l<len;l++){
                ans.push_back(ans[k-l-1]*p[i]);
            }
        }
    }
    for(auto i: ans) cout<<i<<'\n';
    return 0;
}

dfs

这种方法很神奇，放在这里学习一下好了

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int p[50],k[50];

int mode[50];
ll ans=1;
int n;

void dfs(int cur){
    if(cur>n){
        cout<<ans<<'\n';
        return;
    }
    for(int i=1;i<=k[cur];i++){
        dfs(cur+1);
        if(!mode[cur]) ans*=p[cur];
        else ans/=p[cur];
    }
    dfs(cur+1);
    mode[cur]=!mode[cur];
}

int main(){
    ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++){
       cin>>p[i]>>k[i];
    }
    dfs(1);
}