算法分析与设计——实验5：分支限界法

实验五  分支限界法

一、实验目的

        1、理解分支限界算法的基本原理；

        2、理解分支限界算法与回溯算法的区别；

        3、能够使用分支限界算法边界求解典型问题。

二、实验内容及要求

实验要求：通过上机实验进行算法实现，保存和打印出程序的运行结果，并结合程序进行分析，上交实验报告和程序文件。

实验内容：

1、使用分支限界算法解决单源最短路径问题。

2、使用分支限界算法解决0-1背包问题。

3、在N*N的棋盘上放置彼此不受攻击的N个皇后，按照国际象棋的规则，皇后可以攻击与之处于同一行或同一列或同一斜线上的棋子。N皇后的问题等价于在N*N大小的棋盘中放置N个皇后，任何2个皇后不放在同一行或同一列或同一斜线上。使用队列式分支限界法，求出N个皇后的一种放置方案。

*数据输入：由文件input.txt给出输入数据。第一行有1个正整数n。

*结果输出：将计算的彼此不受攻击的n个皇后的一个放置方案输出到文件output.txt。文件的第一行是n个皇后的放置方案。

运行实例：

input.txt

5

output.txt

1 3 5 2 4

三、算法思想分析

1. 分支限界算法

分支限界算法 = 广度优先搜索 + 剪枝策略。

其采用广度优先的策略，依次搜索活结点的所有分支。为了有效选择下一扩展结点，加速搜索的进程，在每一活结点处计算一个函数值（限界函数），并根据这些函数值从当前活结点表中选择一个最有利的结点作为扩展结点，使搜索朝着解空间树上有最优解的分支推进，以便在满足约束条件的解中找出在某种意义下的最优解。其适用于对于存在性问题、最优化问题的求解。

2. 分支界限的基本步骤

（1）设计合适的限界函数

在搜索解空间树时，每个活结点可能有多个孩子结点，我们需要设计合适的限界函数去删除那些不可能产生问题解或最优解的孩子结点，从而提高搜索效率。

（2）组织活结点表

每一个活结点一旦成为扩展结点，就一次性产生它的所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。一直重复上述过程直到找到所需的解或活结点表为空时为止。

从活结点表中选择下一个活结点作为新的扩展结点，不同的活结点表对应不同的分支搜索方式。常见的有以下两种：

  ① 队列式分支限界法：

        a. 将根结点加入活结点队列；

        b. 从活结点队中取出队头结点，作为当前扩展结点；

        c. 对当前扩展结点，先从左到右地产生它的所有孩子结点，用约束条件检查，把所有满足约束条件的孩子结点加入活结点队列；

        d. 重复步骤b和c，直到找到一个解或活结点队列为空为止。

  ② 优先队列式分支限界法：

        a. 计算起始结点（根结点）的优先级并加入优先队列；

        b. 从优先队列中取出优先级最高的结点作为当前扩展结点，使搜索朝着解空间树上可能有最优解的分支推进，以便尽快地找出一个最优解；

        c. 对当前扩展结点，先从左到右地产生它的所有孩子结点，然后用约束条件检查，对所有满足约束条件的孩子结点计算优先级并加入优先队列；

        d. 重复步骤b和c，直到找到一个解或优先队列为空为止。

（3）确定最优解的解向量

        ① 对每个扩展结点保存从根结点到该结点的路径

        ② 在搜索过程中构建搜索经过的树结构

3. 实验内容一：使用分支限界算法解决单源最短路径问题

（1）输入设计：第一行输入顶点数n、边数edge；第二行输入n个顶点的编号；后依次输入edge行所有的路程情况（起点 终点 长度）。

（2）输出设计：给出从首顶点到所有其他顶点的最短距离。

（3）算法设计：

• 算法从图G的源顶点s和空优先队列开始。结点s被扩展后，它的儿子结点a，b，c被依次插入优先队列中；
• 算法从优先队列中取出具有最小当前路长的结点作为当前扩展结点，并依次检查与当前扩展结点相邻的所有顶点；
• 如果从当前扩展结点i到顶点j有边可达，且从源出发，途经顶点i再到顶点j相应的路径的长度小于当前最优路径长度，则将该顶点作为活结点插入到活结点优先队列中。

这个结点的扩展过程一直继续到活结点优先队列为空。

4. 实验内容二：使用分支限界算法解决0-1背包问题

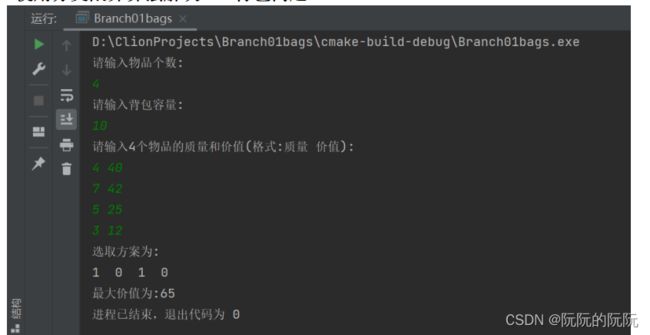
（1）输入设计：第一行输入物品数n，第二行输入背包容量c，接下来的n行依次输入物品的重量weight和价值value。

（2）输出设计：第一行输出选取方案，其中1表示选取，0表示不选取；第二行输出最大价值。

（3）算法设计：如果当前重量+剩余物品中单位重量价值最大的物品的平均价值*剩余重量 > 当前最优价值时，说明我们有必要将右节点加入到队列中，否则剪去右节点。慢慢地更新当前最优价值、当前价值、当前背包容量，取下一活结点作为扩展结点，继续进行遍历，直到我们到达第一个叶结点，即已找到最优解(因为优先队列每次都会弹出优先级最高的活结点)。

5. 实验内容三：N皇后问题

（1）输入设计：input.txt

（2）输出设计：output.txt

（3）算法设计：对当前所处层数的判断：每一层的结尾都压入一个number= -1的节点，每一次在取出队列中的节点时进行判断，如果该节点的nember= -1则当前层数t加1，并且再压入一个nember= -1的节点。然后重新往队列取出下一个节点。

算法终止条件：如果当前取出的节点number为n，则表明已经处理到最后一层，并且最后一层满足约束条件的棋子位置已经都存在队列中了。此时只需把当前节点的数组x赋值给bestx，结束算法。

四、程序代码

1. 使用分支限界算法解决单源最短路径问题

#include 
#include 
using namespace std;

typedef struct ArcCell {
    int weight;         //记录权值
    int min_length;     //存储最短路径长度
} AdjMaxtrix[100][100];

typedef struct {
    int data;           //顶点编号
    int length;         //起始顶点到data编号顶点的最短路径
}VerType;

typedef struct {
    VerType vexs[100];   //顶点向量
    AdjMaxtrix arcs;
    int vertex;         //顶点数
    int edge;           //边的数量
}Graph;

Graph G;
queue q;

void CreateGraph() {
    int m, n, t;
    cout << "请输入顶点数和边数: " <> G.vertex >> G.edge;
    cout << "输入顶点编号:" << endl;
    for (int i = 1; i <= G.vertex; i++) {
        cin >> G.vexs[i].data;
        G.vexs[i].length = 10000;
    }

    for (int i = 1; i <= G.vertex; i++)
        for (int j = 1; j <= G.vertex; j++) {
            G.arcs[i][j].weight = 0;
        }
    cout << "请输入所有路程的起点、终点和长度(格式:起点 终点 长度):" << endl;
    for (int i = 1; i <= G.edge; i++) {
        cin >> m >> n >> t;
        G.arcs[m][n].weight = 1;
        G.arcs[m][n].min_length = t;
    }
}

int nextWeight(int v, int w) {
    for (int i = w + 1; i <= G.vertex; i++)
        if (G.arcs[v][i].weight)
            return i;       //返回已有的边中序号最前的
        return 0;           //未找到符合条件结点返回最初的结点
}

void ShortestPaths(int v) {
    int k = 0;                  //从首个节点开始访问，k记录想要访问结点的位置
    int t;
    G.vexs[v].length = 0;
    q.push(G.vexs[v].data);
    while (!q.empty()) {         //队列q不为空的时候执行循环
        t = q.front();           //t为队列中第一个元素，也就是最先要被弹出的结点，返回值是其编号，第一次执行这一步时是 G.vexs[1].data，初始结点的编号
        k = nextWeight(t, k);    //k不断更新为已有的边中序号最前的
        while (k != 0) {
            if (G.vexs[t].length + G.arcs[t][k].min_length <= G.vexs[k].length) {
                //减枝操作
                G.vexs[k].length = G.vexs[t].length + G.arcs[t][k].min_length;
                q.push(G.vexs[k].data);
            }
            k = nextWeight(t, k);   //k不断更新为已有的边中序号最前的
        }
        q.pop();
    }
}

void Print() {
    for (int i = 2; i <= G.vertex; i++)
cout << "顶点1到顶点" << i << "的最短路径长为:" << G.vexs[i].length << endl;
}

int main() {
    CreateGraph();
    ShortestPaths(1);
    Print();
    return 0;
}

2. 使用分支限界算法解决0-1背包问题

#include
#include
#include
using namespace std;

int n;  //物品个数
int c;  //背包容量

//定义物品结构体
struct Item  {
    int ItemID;  //编号
    int value;   //价值
    int weight;  //重量
    int ratio;   //价值比
};

//定义搜索节点
struct Node {
    int value;   //到该结点的总价值
    int weight;  //到该结点的总重量
    int bound;   //到该结点的子树能达到的价值上界
    int level;   //层次
    struct Node* parent; //父节点

    Node() {
        value = 0;
        weight = 0;
        level = 0;
        parent = 0;
        bound = 0;
    }
};

//按照大顶堆的形式存放
struct cmp {
    bool operator()(Node* a, Node* b) {
        return a->bound < b->bound;
    }
};

int searchCount = 0;
int maxSize = 0;
bool Itemcmp(Item item1, Item item2);     //比较函数
int branchAndBound(Item items[], int c);  //分支限界法
float maxBound(Node* node, Item items[], int c);  //限界函数

int main() {
    int maxValue;
    cout << "请输入物品个数:" << endl;
    cin >> n;
    cout << "请输入背包容量:" <> c;
    int* w = new int[n];
    int* v = new int[n];
    cout << "请输入" << n << "个物品的质量和价值(格式:质量 价值):" << endl;
    for (int i = 0; i < n; i++)
    {
        cin >> w[i] >> v[i];
    }

    Item* items = new Item[n];  //定义物品结构体
    //初始化结构体数组
    for (int i = 0; i < n; i++) {
        items[i].ItemID = i;
        items[i].value = v[i];
        items[i].weight = w[i];
        items[i].ratio = 1.0 * v[i] / w[i];
    }
    sort(items, items + n, Itemcmp);   //按价值率排序

    cout << "选取方案为:" << endl;
    maxValue = branchAndBound(items, c);
    cout << "最大价值为:" << maxValue;
}

//比较函数
bool Itemcmp(Item item1, Item item2) {
    return item1.ratio > item2.ratio;
}

//分支限界函数
int branchAndBound(Item items[], int c) {
    int* x = new int[n];
    for (int i = 0; i < n; i++) {
        x[i] = 0;
    }

    int maxValue;  //保存最大价值
    Node* maxNode = new Node();  //保存当前最大价值节点
    priority_queue, cmp> maxQueue;  //最大价值优先队列
    Node* firstNode, * curNode;

    searchCount = 1;
    firstNode = new Node();
    firstNode->bound = maxBound(firstNode, items, c);
    firstNode->parent = NULL;
    maxQueue.push(firstNode);
    maxValue = 0;
    maxNode = firstNode;
    while (!maxQueue.empty()) {
        curNode = maxQueue.top();
        maxQueue.pop();
        //扩展左孩子
        if (curNode->weight + items[curNode->level].weight <= c) {
            Node* leftNode = new Node();
            leftNode->value = curNode->value + items[curNode->level].value;
            leftNode->weight = curNode->weight + items[curNode->level].weight;
            leftNode->level = curNode->level + 1;
            leftNode->parent = curNode;
            leftNode->bound = curNode->bound;
            if (leftNode->level < n) {
                maxQueue.push(leftNode);
                searchCount++;
            }
            if (maxValue < leftNode->value) {
                maxValue = leftNode->value;
                maxNode = leftNode;
            }
        }

        //扩展右孩子节点
        if (maxBound(curNode, items, c) > maxValue) {
            Node* rightNode = new Node();
            rightNode->value = curNode->value;
            rightNode->weight = curNode->weight;
            rightNode->level = curNode->level + 1;
            rightNode->parent = curNode;
            rightNode->bound = maxBound(rightNode, items, c);
            if (rightNode->level < n) {
                maxQueue.push(rightNode);
                searchCount++;
            }
        }
        if (maxQueue.size() > maxSize) {
            maxSize = maxQueue.size();
        }
    }
    curNode = maxNode;
    while (curNode) {
        int tempValue = curNode->value;
        curNode = curNode->parent;
        if (curNode && curNode->value != tempValue) {
            x[items[curNode->level].ItemID] = 1;
        }
    }
    for (int i = 0; i < n; i++) {
        cout << x[i] << "  ";
    }
    cout << endl;
    return maxValue;
}

//限界函数
float maxBound(Node* node, Item items[], int c) {
    float maxValue;
    int restCapacity;  //背包剩余容量
    int i;

    maxValue = node->value;
    restCapacity = c - node->weight;
    i = node->level;

    while (iitems[i].weight) {
        maxValue += items[i].value;
        restCapacity -= items[i].weight;
        i++;
    }
    if (restCapacity != 0) {
        maxValue += restCapacity * items[i].ratio;
    }
    return maxValue;
}

3. N皇后问题

#include
#include
#include
#include
#include
using namespace std;

struct Node {
    int number;
    vectorx;
};

class Queen{
    friend int nQueen(int);
public:
    bool Place(Node q,int n);
    void Research();
    int n;
    int *bestx;
};

bool Queen::Place(Node q,int n) {
    for(int j=1;jQ;
    Node sign;
    sign.number=-1;
    Q.push(sign);
    int t=1;
    Node Ew;
    Ew.number=0;
    while(1) {
        for(int k=1;k<=n;k++){
            Node q;
            q.number=t;
            q.x.push_back(0);
            for(int i=1;i> N;
    cinfile.close();

    ofstream outfile;
    outfile.open("output.txt",ios::out);

    nQueen(N,outfile);

    outfile.close();
    return 0;
}

五、结果运行与分析

1. 使用分支限界算法解决单源最短路径问题

2. 使用分支限界算法解决0-1背包问题

3. N皇后问题

六、心得与体会

本次是算法分析与设计的最后一次实验，主要是应用分支限界法分别解决单源最短路径问题、0-1背包问题和N皇后问题。

分支限界法是在广度优先搜索的基础上进行剪枝策略。它与回溯法在求解目标和搜索方式上存在不同。回溯法的求解目标是找出解空间树中满足约束条件的所有解，而分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解；回溯法以深度优先的方式搜索解空间树，而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。

其主要步骤为：①定义解空间（对解编码）；②确定解空间的树结构；③按照BFS等方式搜索：a.每个活结点仅有一次机会变成扩展结点、b.由扩展结点生成一步可达的新结点、c.在新节点中，用限界策略删除不可能导出最优解的结点、d.将余下的新节点加入活动表（队列）中、e. 用分支策略从活动表中选择结点再扩展、f.知道活动表为空；④利用先进先出队列（FIFO）、优先队列的活结点扩充方式求解。

至此，算法分析与设计的课程就到了尾声。本学期，我们学习了很多实用的算法，让我受益匪浅；同时也对递归与分析、动态规划算法、贪心算法、回溯算法和分支限界算法进行了上机实验，得到了较好的巩固。