代码随想录-Day32
122. 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。

// 贪心思路
class Solution {
public int maxProfit(int[] prices) {
int result = 0;
for (int i = 1; i < prices.length; i++) {
result += Math.max(prices[i] - prices[i - 1], 0);
}
return result;
}
}
这段代码实现的是计算股票买卖收益的最大利润,这是一个经典的动态规划问题,但这里采用了一种贪心的解法。这个解法是用于解决“在股票价格数组中,只能进行一次买入和一次卖出的情况下,求最大利润”的问题。
解释代码:
- 函数签名:
public int maxProfit(int[] prices)接受一个整数数组prices,表示股票每天的价格。 - 初始化变量
result = 0用来累计最大利润。 - 使用一个
for循环,从数组的第二个元素开始遍历到末尾(i = 1到prices.length - 1)。- 在每次循环中,计算当前天数
i的价格与前一天i - 1的价格之差prices[i] - prices[i - 1]。 - 使用
Math.max()函数取这个差值与0的最大值。这样可以确保只有当当天价格高于前一天时(即可以盈利时),才将差值累加到结果中。如果当天价格比前一天低,则不进行交易,结果增加0。 - 每次迭代的结果累加到
result中。
- 在每次循环中,计算当前天数
- 循环结束后,返回累计的最大利润
result。
总结:
这段代码提供了一个简洁的贪心策略来解决股票交易中的最大利润问题,特别适用于只允许进行一次买入和一次卖出的情况。通过逐天检查能否获得正利润,并立即获取这些利润,从而避免了复杂的动态规划状态维护,降低了算法的时间复杂度至O(n),其中n为股票价格数组的长度。
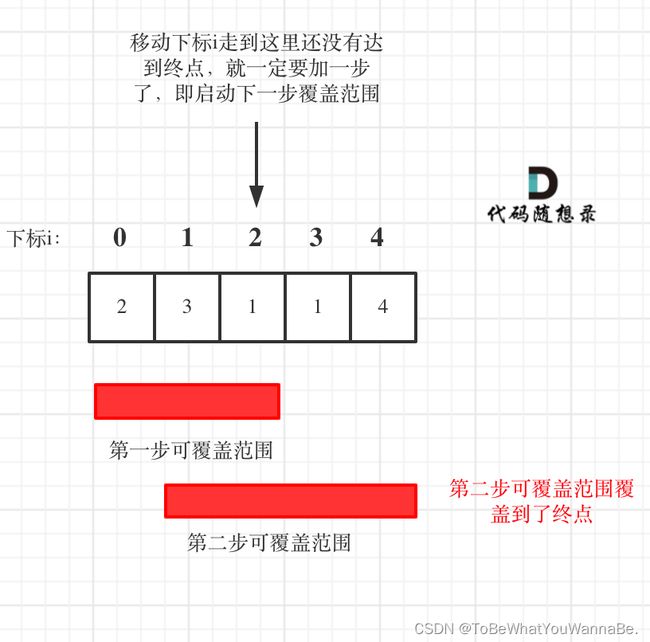
55. 跳跃游戏
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
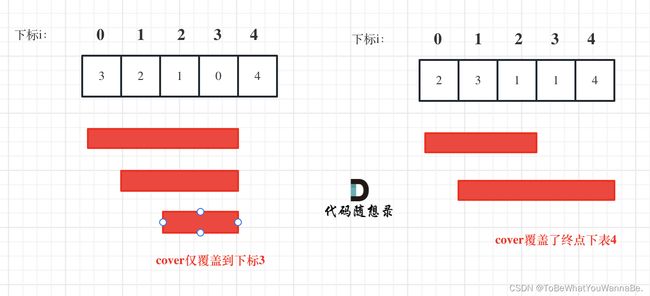
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
class Solution {
public boolean canJump(int[] nums) {
if (nums.length == 1) {
return true;
}
//覆盖范围, 初始覆盖范围应该是0,因为下面的迭代是从下标0开始的
int coverRange = 0;
//在覆盖范围内更新最大的覆盖范围
for (int i = 0; i <= coverRange; i++) {
coverRange = Math.max(coverRange, i + nums[i]);
if (coverRange >= nums.length - 1) {
return true;
}
}
return false;
}
}
这段代码是用于解决“跳跃游戏”问题的,该问题是判断在一个给定的非负整数数组 nums 中,初始从数组的第一个位置(下标为0)出发,你是否能够跳到最后一个位置。数组中的每个元素 nums[i] 表示你在该位置上能够跳跃的最大长度。
代码解释:
- 函数签名:
public boolean canJump(int[] nums)接受一个非负整数数组nums作为输入参数。 - 特殊情况处理:如果数组长度为1,即只有一个位置,自然能跳到最后,所以直接返回
true。 - 初始化
coverRange = 0,这个变量表示当前能覆盖的最远距离的结束下标。 - 使用
for循环,迭代的条件是i <= coverRange,意味着只要当前位置在已知可达范围内,就继续尝试扩展这个范围。- 在循环体内,用
Math.max()更新coverRange,使其成为当前下标i加上从该位置可跳跃的最大距离nums[i]的较大值。这样可以确保coverRange总是表示当前位置能到达的最远边界。 - 如果在某次迭代中,发现
coverRange已经大于等于数组最后一个元素的下标(即coverRange >= nums.length - 1),说明可以跳到最后的位置了,因此提前返回true。
- 在循环体内,用
- 循环结束后,如果没有提前返回,说明没有找到能跳到数组末尾的路径,返回
false。
总结:
这段代码实现了一个有效且节省空间的解决方案来判断在给定条件下能否完成跳跃游戏。其核心思想是动态维护一个不断扩大的“覆盖范围”,并利用这个范围来决定是否需要继续探索后面的元素,避免了冗余的循环迭代,提高了效率。
45. 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
方法一:
// 版本一
class Solution {
public int jump(int[] nums) {
if (nums == null || nums.length == 0 || nums.length == 1) {
return 0;
}
//记录跳跃的次数
int count=0;
//当前的覆盖最大区域
int curDistance = 0;
//最大的覆盖区域
int maxDistance = 0;
for (int i = 0; i < nums.length; i++) {
//在可覆盖区域内更新最大的覆盖区域
maxDistance = Math.max(maxDistance,i+nums[i]);
//说明当前一步,再跳一步就到达了末尾
if (maxDistance>=nums.length-1){
count++;
break;
}
//走到当前覆盖的最大区域时,更新下一步可达的最大区域
if (i==curDistance){
curDistance = maxDistance;
count++;
}
}
return count;
}
}
这段代码是用于解决“跳跃游戏 II”问题的,目标是在给定的非负整数数组 nums 中,找到达到数组最后一个位置所需的最少跳跃次数。数组中的每个元素 nums[i] 表示从位置 i 可以跳跃的最大长度。
代码解释:
- 函数签名:
public int jump(int[] nums)接受一个非负整数数组nums作为输入参数。 - 首先检查特殊情况:如果数组为空、长度为0或1,直接返回0,因为不需要跳跃即可到达终点。
- 初始化三个变量:
count=0,记录跳跃的总次数。curDistance=0,表示当前能到达的最远位置的下标。maxDistance=0,表示在当前位置能跳跃到的最远位置的下标。
- 使用一个
for循环遍历数组。- 在循环内,首先使用
Math.max()更新maxDistance,确保它始终表示当前可达的最远边界。 - 当
maxDistance大于等于数组最后一个元素的下标(即maxDistance >= nums.length - 1),说明下一步就可以到达终点,此时更新count并跳出循环。 - 当遍历到的位置
i等于当前的覆盖最大区域curDistance时,说明已经走到了当前能跳的最远地方,需要进行下一次跳跃,此时更新curDistance为maxDistance(即下一步能到达的最远位置),并将跳跃次数count加1。
- 在循环内,首先使用
- 循环结束后,返回跳跃的次数
count。
总结:
这个版本的解决方案有效地利用了贪心策略,通过维护当前覆盖的最大区域和下一个可能的最大覆盖区域来减少跳跃次数,确保以最少的步数到达数组的末尾。这种方法避免了暴力搜索所有可能的跳跃路径,提高了算法效率。
方法二:
// 版本二
class Solution {
public int jump(int[] nums) {
int result = 0;
// 当前覆盖的最远距离下标
int end = 0;
// 下一步覆盖的最远距离下标
int temp = 0;
for (int i = 0; i <= end && end < nums.length - 1; ++i) {
temp = Math.max(temp, i + nums[i]);
// 可达位置的改变次数就是跳跃次数
if (i == end) {
end = temp;
result++;
}
}
return result;
}
}
这个版本的代码同样解决了“跳跃游戏 II”问题,即确定到达数组最后一个位置所需的最少跳跃次数。其逻辑和之前版本相似,但结构稍有不同,以下是详细解释:
代码解释:
- 函数签名:
public int jump(int[] nums)接受一个非负整数数组nums作为输入参数。 - 初始化两个变量:
end=0,表示当前能到达的最远位置的下标。temp=0,用于记录在遍历过程中能到达的下一个最远位置的临时下标。
- 使用一个
for循环遍历数组,循环条件结合了当前位置i的限制以及是否已到达或超过数组最后一个元素的前一位(end < nums.length - 1),这样可以在到达终点前停止循环。- 在循环内部,首先使用
Math.max()更新temp,保证它保存从当前位置i出发能跳跃到的最远位置。 - 当
i等于当前的最远覆盖范围end时,说明已经到达了一个阶段的最远可到达点,需要进行下一次跳跃。这时,更新end为temp(即下一步能达到的最远位置),同时增加跳跃次数result。
- 在循环内部,首先使用
- 循环结束后,返回跳跃次数
result。
总结:
此版本代码仍然是贪心策略的应用,通过维护当前可达到的最远范围以及下一步可达的最大范围来确定最小跳跃次数。与版本一相比,它的循环条件更加紧凑,并且在更新 end 和计数时的逻辑更直接地反映了“到达一个阶段的边界后即进行跳跃”的思想。这种实现方式同样高效,清晰地表达了跳跃过程中的关键状态转移。
1005. K 次取反后最大化的数组和
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
输入:nums = [4,2,3], k = 1
输出:5
解释:选择下标 1 ,nums 变为 [4,-2,3] 。
示例 2:
输入:nums = [3,-1,0,2], k = 3
输出:6
解释:选择下标 (1, 2, 2) ,nums 变为 [3,1,0,2] 。
示例 3:
输入:nums = [2,-3,-1,5,-4], k = 2
输出:13
解释:选择下标 (1, 4) ,nums 变为 [2,3,-1,5,4] 。
class Solution {
public int largestSumAfterKNegations(int[] nums, int K) {
// 将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
nums = IntStream.of(nums)
.boxed()
.sorted((o1, o2) -> Math.abs(o2) - Math.abs(o1))
.mapToInt(Integer::intValue).toArray();
int len = nums.length;
for (int i = 0; i < len; i++) {
//从前向后遍历,遇到负数将其变为正数,同时K--
if (nums[i] < 0 && K > 0) {
nums[i] = -nums[i];
K--;
}
}
// 如果K还大于0,那么反复转变数值最小的元素,将K用完
if (K % 2 == 1) nums[len - 1] = -nums[len - 1];
return Arrays.stream(nums).sum();
}
}
这段代码是解决“数组中K次翻转后的最大和”问题的Java实现。给定一个整数数组 nums 和一个整数 K,你可以将数组中的任意元素更改 K 次,每次更改可以选择一个元素并将其乘以 -1。目标是经过最多 K 次翻转后,得到数组的最大可能和。下面是代码的详细解释:
代码解释:
-
绝对值排序:首先,使用 Java 8 的 Stream API 对数组
nums中的元素按其绝对值进行降序排序。这样做是为了优先处理绝对值较大的负数,因为在翻转次数有限的情况下,改变绝对值较大的负数对总和的增益更大。 -
翻转负数:接下来,遍历排序后的数组。如果当前元素为负数且翻转次数
K大于0,就将该元素乘以-1(即翻转其符号),并减少K的计数。这样可以尽可能多地将负数转换为正数,以增加总和。 -
处理剩余的翻转次数:如果在遍历完数组后
K仍有剩余,说明所有的负数都已被翻转完了。此时,若K是奇数,说明还需要进行一次翻转操作,最优选择是翻转当前数组中的最小元素(由于数组已按绝对值降序排列,最小元素即为数组最后一个元素)。如果K是偶数,则无需额外操作,因为连续的翻转会取消效果。 -
计算最终和:最后,使用
Arrays.stream(nums).sum()计算处理后的数组元素总和并返回。
总结:
这段代码通过优先翻转绝对值较大的负数,并合理处理剩余的翻转次数,实现了在给定 K 次翻转限制下,数组元素和的最大化。其核心思路在于理解如何高效地利用每一次翻转机会,特别是排序步骤对于优化结果至关重要。