【图论】最短路算法
【图论】最短路算法
文章目录
-
- 【图论】最短路算法
-
- 1. Dijkstra
- 2. Bellman-Ford
- 3. Floyd
- 4. A*
- 5. matlab求最短路
今天是图论的学习,就从最短路算法开始叭
1. Dijkstra
Dijkstra算法是典型的单源最短路算法,即求图中一个点到其他所有点的最短路径的算法,时间复杂度 O ( n 2 ) O(n^2) O(n2)
Dijkstra算法算是贪心思想实现的,图不能有负权边,其核心要点为:
每次从 「未求出最短路径的点」中 取出 「离起点距离最短」 路径的点,并以这个点为当前节点 刷新「未求出最短路径的点」的距离
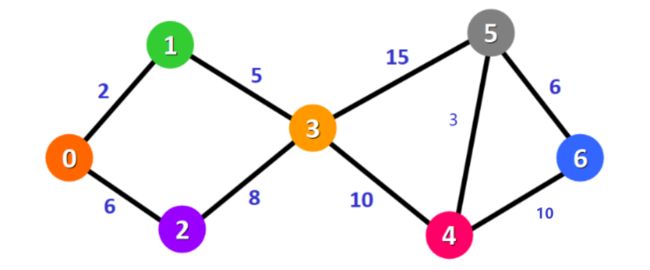
以下图为例:
Dijkstra 算法将会寻找出图中 节点0 到所有其他节点的最短路径。
起点到每个点的距离:
| 节点 | 当前节点 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|
| step1 | − - − | 0 0 0 | ∞ \infty ∞ | ∞ \infty ∞ | ∞ \infty ∞ | ∞ \infty ∞ | ∞ \infty ∞ | ∞ \infty ∞ |
| step2 | 0 0 0 | 0 0 0 | 2 2 2 | 6 6 6 | ∞ \infty ∞ | ∞ \infty ∞ | ∞ \infty ∞ | ∞ \infty ∞ |
| step3 | 1 1 1 | 0 0 0 | 2 2 2 | 6 6 6 | 7 7 7 | ∞ \infty ∞ | ∞ \infty ∞ | ∞ \infty ∞ |
| step4 | 2 2 2 | 0 0 0 | 2 2 2 | 6 6 6 | 7 7 7 | ∞ \infty ∞ | ∞ \infty ∞ | ∞ \infty ∞ |
| step5 | 3 3 3 | 0 0 0 | 2 2 2 | 6 6 6 | 7 7 7 | 17 17 17 | 22 22 22 | ∞ \infty ∞ |
| step6 | 4 4 4 | 0 0 0 | 2 2 2 | 6 6 6 | 7 7 7 | 17 17 17 | 20 20 20 | 27 27 27 |
| step7 | 5 5 5 | 0 0 0 | 2 2 2 | 6 6 6 | 7 7 7 | 17 17 17 | 20 20 20 | 26 26 26 |
| step8 | 6 6 6 | 0 0 0 | 2 2 2 | 6 6 6 | 7 7 7 | 17 17 17 | 20 20 20 | 26 26 26 |
代码
def dijkstra(s):
# 标记数组:used[v]值为False说明改顶点还没有访问过,在S中,否则在U中!
used = [False for _ in V]
# 距离数组:distance[i]表示从源点s到i的最短距离,先把所有节点的距离初始化为无穷
distance = [float('inf') for _ in V]
distance[s] = 0
while True:
# v在这里相当于是一个哨兵,对包含起点s做统一处理!
v = -1
# 从未使用过的顶点中选择一个距离最小的顶点
for u in V:
if not used[u] and (v == -1 or distance[u] < distance[v]):
v = u
if v == -1:
# 说明所有顶点都维护到S中了!
break
# 将选定的顶点加入到S中, 同时进行距离更新
used[v] = True
# 更新U中各个顶点到起点s的距离。
for u in V:
distance[u] = min(distance[u], distance[v] + cost[v][u])
2. Bellman-Ford
Bellman-Ford是单源最短路径问题的一种算法。它的原理是对图进行 n − 1 n-1 n−1 次松弛操作,得到所有可能的最短路径。
其优于Dijkstra算法的方面是边的权值可以为负数、实现简单,缺点是时间复杂度过高。
实现步骤:
- 初始化:源点到自己的距离为 0,其他点到源点的距离为正无穷。
- 第一次迭代:找到不超过1 条边的最短路
- 第二次迭代:找到不超过2 条边的最短路
- ……
- 第n次迭代:找到不超过 n − 1 n-1 n−1条边的最短路
代码:
def bellman_ford(graph, source):
dist = {}
p = {}
max = 10000
for v in graph:
dist[v] = max #赋值为负无穷完成初始化
p[v] = None
dist[source] = 0
for i in range(len( graph ) - 1):
for u in graph:
for v in graph[u]:
if dist[v] > graph[u][v] + dist[u]:
dist[v] = graph[u][v] + dist[u]
p[v] = u #完成松弛操作,p为前驱节点
for u in graph:
for v in graph[u]:
if dist[v] > dist[u] + graph[u][v]:
return None, None #判断是否存在环路
return dist, p
int dist[N],backup[N];//dist距离,backup用来存上一次的结果。
struct edge//用来存边
{
int a;
int b;
int w;
}Edge[M];
int Bellman_Ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;//初始化
for(int i = 0 ; i < k ; i++)//遍历k次
{
memcpy(backup,dist,sizeof dist);//存上一次答案。
for(int j = 0 ; j < m ; j++)
{
int a = Edge[j].a, b = Edge[j].b, w = Edge[j].w;
dist[b] = min(dist[b],backup[a] + w);
}//遍历所有边
}
if(dist[n] > 0x3f3f3f3f/2) return -1;
/*这里不像Dijkstra写等于正无穷是因为可能有负权边甚至是负环的存在,
使得“正无穷”在迭代过程中受到一点影响。*/
return dist[n];
}
3. Floyd
Floyd 算法是典型的多源最短路算法, 求 所有点到所有点 的最短路径的算法
核心要点:
要点:以每个点为 「中转站」 , 刷新所有 「入度」 和 「出度」 的距离。
遍历每一个顶点 --> 遍历点的每一个入度 --> 遍历每一个点的出度,以这个点为「中转站」距离更短就刷新距离
(比如 B 点为中转站 AB + BD < AD 就刷新 A 到 D 的距离)
代码
for k in range(n):
for i in range(n):
for j in range(n):
graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
4. A*
A*算法是一种启发式搜索算法,利用合适的启发函数,全面评估各扩展搜索节点的代价值,通过比较扩展节点代价值的大小,选择价值最小的点加以扩展,直到找到目标节点为止。
和 Dijkstra 算法相比,A* 采用启发式的搜索策略,能够更快地搜索出最短路径
核心的模型评估函数是:
f ( n ) = g ( n ) + h ( n ) f(n)=g(n)+h(n) f(n)=g(n)+h(n)
- f ( n ) f(n) f(n) —— 总代价函数
- g ( n ) g(n) g(n) —— 一起点到结点n的真实距离函数
- h ( n ) h(n) h(n) —— 结点n到终点的估计距离的启发函数
算法流程:
- 用优先队列定义一个
openList 表: 记录准备处理的点,根据f(n)升序排序 - 用字典来定义一个
closeList 表: 记录最短路径上的所有点的信息
- 为了要保证找到最优解,要使启发函数 h ( n ) < = h ∗ ( n ) h(n)<= h^*(n) h(n)<=h∗(n) ( h ∗ ( n ) h^*(n) h∗(n)为节点到终点的真实距离)
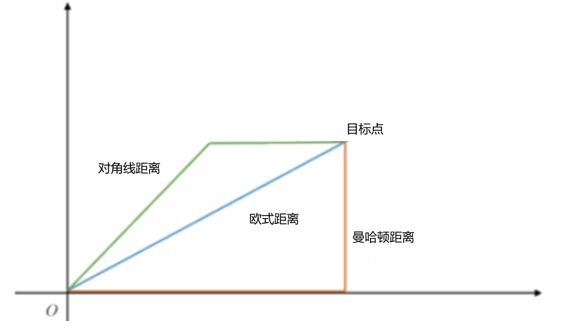
估计距离的对比
- 允许4邻域(即上下左右)的移动,使用曼哈顿距离
- 允许8邻域(上下左右,左上右上左下右下)的移动,使用对角线距离
- 允许任何方向的移动,使用欧几里得距离
代码
def planning(self, sx, sy, gx, gy):
# 设置起点,先获得起点所在的格子,然后起点的花费初始化为0,父节点初始化为-1
start_node = self.Node(self.get_xy(sx, self.min_x), self.get_xy(sy, self.min_y), 0.0, -1)
# 设置终点,先获得终点所在的格子,然后起点的花费初始化为0,父节点初始化为-1
goal_node = self.Node(self.get_xy(gx,self.min_x), self.get_xy(gy, self.min_y), 0.0, -1)
start_node.distance = self.get_distance(goal_node, start_node) # 初始化起点的估计距离
q = PriorityQueue() # 定义一个优先队列
q.put(start_node) # 起点入队
closed_set = {}
dis = {} # 记录起点到每个点的距离
n_id = self.get_node(start_node)
dis[n_id] = 0
while not q.empty():
current = q.get() # 获取队头元素加出队
id = self.get_node(current)
if id in closed_set: continue
closed_set[id] = current # 把这个点加入close_set中
# 如果到达了终点
if current.x == goal_node.x and current.y == goal_node.y:
goal_node.parent_index = current.parent_index
goal_node.cost = current.cost
break
for i,_ in enumerate(self.motion):
node = self.Node(current.x + self.motion[i][0], current.y + self.motion[i][1], current.cost + self.motion[i][2], id)
now_id = self.get_node(node)
# 如果close_set中已经有它了, 不会重复添加和更新
if now_id in closed_set: continue
# 如果不满足合法条件
if not self.verify_node(node): continue
node.distance = node.cost + self.get_distance(node,goal_node)
if(now_id not in dis):
dis[now_id] = node.cost
q.put(node)
elif(node.cost < dis[now_id]):
dis[now_id] = node.cost
q.put(node)
# 获得路径
rx, ry = self.get_path(goal_node, closed_set)
return rx, ry
5. matlab求最短路
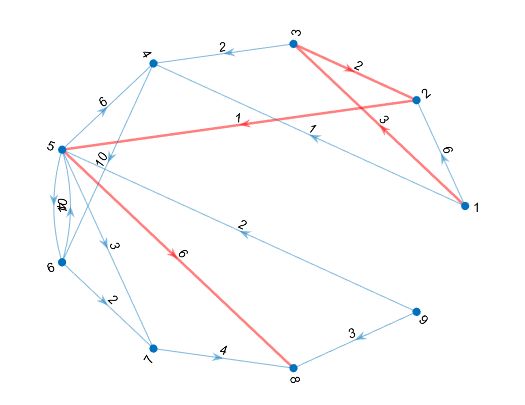
有向图最短路
% 图的邻接矩阵
E = [1,2,6;1,3,3;1,4,1;2,5,1;3,2,2;3,4,2;4,6,10;5,4,6;
5,6,4;5,7,3;5,8,6;6,5,10;6,7,2;7,8,4;9,5,2;9,8,3];
% 边的一端,边的另一端,边的权值
G = digraph(E(:,1),E(:,2),E(:,3));
% 找出最短路和花费的费用
[path,d] = shortestpath(G,1,8,'method','positive');
% 画出图
p = plot(G,'EdgeLabel',G.Edges.Weight,'Layout','circle');
% 高亮出最短路径
highlight(p,path,'EdgeColor','red','LineWidth',1.5);
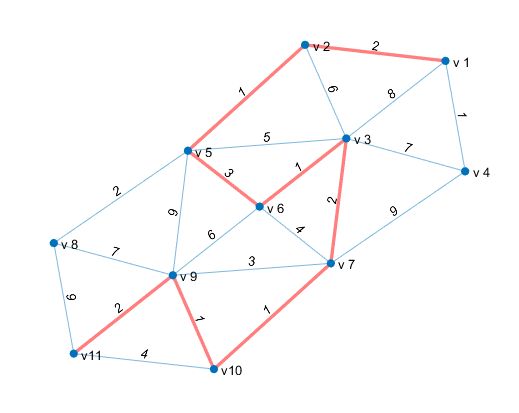
a = zeros(11);
a(1,2)=2;a(1,3)=8;a(1,4)=1;
a(2,3)=6;a(2,5)=1;
a(3,4)=7;a(3,5)=5;a(3,6)=1;a(3,7)=2;
a(4,7)=9;a(5,6)=3;a(5,8)=2;a(5,9)=9;
a(6,7)=4;a(6,9)=6;a(7,9)=3;a(7,10)=1;
a(8,9)=7;a(8,11)=9;
a(9,10)=1;a(9,11)=2;a(10,11)=4;
s=cellstr(strcat('v',int2str([1:11]'))); % 顶点字符串
G=graph(a,s,'Upper'); % 利用邻接矩阵的上三角元素构造无向图
[p,d]=shortestpath(G,1,11); % 求最短路径和最短距离
h = plot(G,'EdgeLabel',G.Edges.Weight); % 画无向图
highlight(h,p,'EdgeColor','r','LineWidth',2); % 最短路径加粗