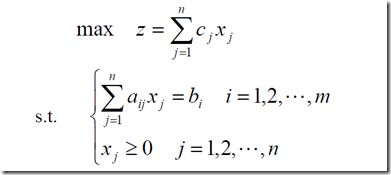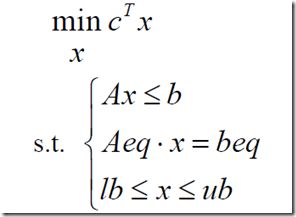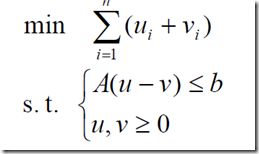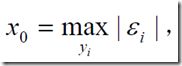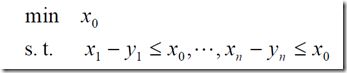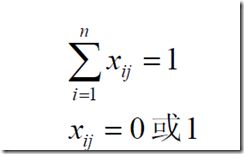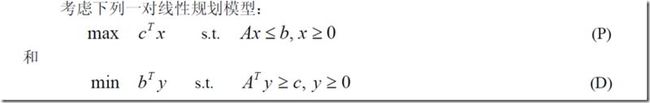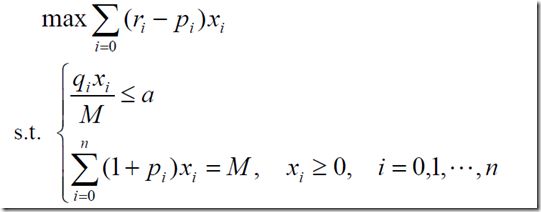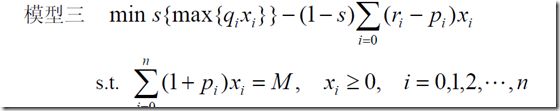建模算法(一)——线性规划
一、解决问题
主要是安排现有资源(一定),取得最好的效益的问题解决,而且约束条件都是线性的。
二、数学模型
1、一般数学模型
2、MATLAB数学模型
其中c,x都是列向量,A,Aeq是一个合适的矩阵,b,beq是合适的列向量。然后lb和ub是下限和上线(但是请注意= =,lb是一个变量的名字)
三、相关方程解法
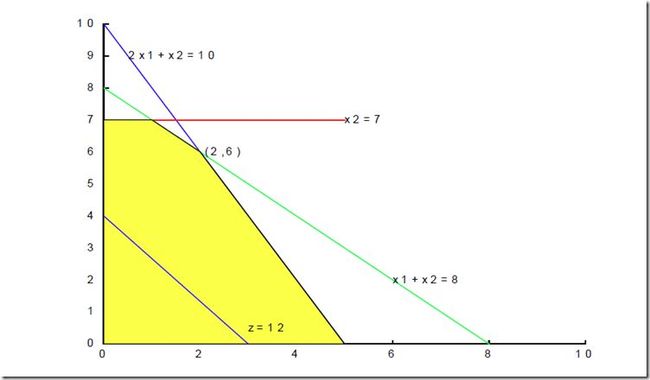
1、图解法,画出可行域,这个可以进行编程进行实现、
2、直接使用MATLAB的相关方法进行解题、
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,Xo,OPTIONS)
其中fval返回的是目标函数的值,然后x则是返回取到fval时x的对应的值,然后LB和UB是对应x的上界和下界(可以省略),x0是x的初始值(暂时可以忽略)
OPTIONS是控制参数。
四、一些其他问题转换成线性规划
1、绝对值之和最小
2、两个数的差的绝对值,在xi固定时,取得max,之后在去定yi
五、一些线性规划可以解决的实际问题
1、生产力有限,要求取得最大收益
2、运输问题(产销问题)
要求运输费用最小
在这里需要记得有一个很重要的等式,就是所有产地送出去的等于所有销售地收到的
3、指派问题
要求花费的工作时间要最短
(2)求解指派问题的匈牙利算法、
首先我们要知道对与系数矩阵C由这样的性质,同时对每一行(列)加上或者减去同样的一个数,得到的新矩阵和原矩阵的指派问题具有相同的最优指派。
一般步骤是:
a、每行每列消除最小的数字,使得出现能够出现N(与矩阵大小相同)个位于不同行不同列的零元素,选定就是最优解。
b、如果上一步骤没办法直接完成,则、
4、对偶理论(与反函数相比较)
最重要的是掌握其性质,可以用来检验是不是最优解、、
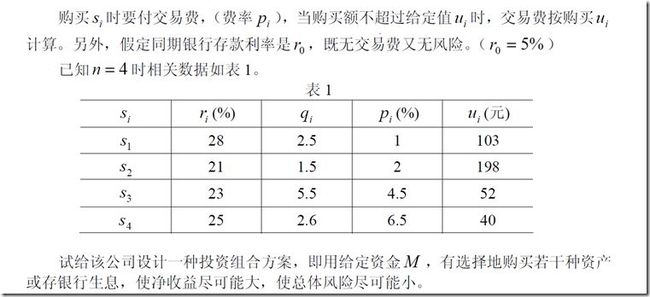
5、投资的收益和风险(主要多目标函数如何并成一个目标函数)
下一步主要是设立变量(这是数学建模中一步很关键的地方,你指标选的好,方程就好列好解,否则。。。。)
之后就是加入限定,一些理想化的假设
然后写出方程
其中第一个目标函数为收益,第二个为风险。
下一步就是化简目标函数
(1)固定风险水平,优化收益
(2)固定盈利水平,极小化风险
(3)同时考虑两个,这样的话需要加入一个权重s。