AtCoder Beginner Contest 369（ABCDEFG题）视频讲解

A - 369

Problem Statement

You are given two integers $A$ and $B$.
How many integers $x$ satisfy the following condition?
Condition: It is possible to arrange the three integers $A$, $B$, and $x$ in some order to form an arithmetic sequence.
A sequence of three integers $p$, $q$, and $r$ in this order is an arithmetic sequence if and only if $q-p$ is equal to $r-q$.

Constraints

$1\le A,B\le 100$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$A$ $B$

Output

Print the number of integers $x$ that satisfy the condition in the problem statement.
It can be proved that the answer is finite.

Sample Input 1

5 7

Sample Output 1

3

The integers $x=3,6,9$ all satisfy the condition as follows:
When $x=3$, for example, arranging $x,A,B$ forms the arithmetic sequence $3,5,7$.
When $x=6$, for example, arranging $B,x,A$ forms the arithmetic sequence $7,6,5$.
When $x=9$, for example, arranging $A,B,x$ forms the arithmetic sequence $5,7,9$.
Conversely, there are no other values of $x$ that satisfy the condition.
Therefore, the answer is $3$.

Sample Input 2

6 1

Sample Output 2

2

Only $x=-4$ and $11$ satisfy the condition.

Sample Input 3

3 3

Sample Output 3

1

Only $x=3$ satisfies the condition.

Solution

具体见文末视频。

---

Code

#include 
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int a, b;
	cin >> a >> b;
	if (a > b) swap(a, b);

	set<int> S;
	if ((a + b) % 2 == 0) S.insert(a + b >> 1);
	S.insert(b + b - a), S.insert(a - (b - a));

	cout << S.size() << endl;

	return 0;
}

B - Piano 3

Problem Statement

Takahashi has a piano with $100$ keys arranged in a row.
The $i$-th key from the left is called key $i$.
He will play music by pressing $N$ keys one by one.
For the $i$-th press, he will press key $A_i$, using his left hand if $S_i=$ L, and his right hand if $S_i=$ R.
Before starting to play, he can place both of his hands on any keys he likes, and his fatigue level at this point is 0.
During the performance, if he moves one hand from key $x$ to key $y$, the fatigue level increases by $|y-x|$ (conversely, the fatigue level does not increase for any reason other than moving hands).
To press a certain key with a hand, that hand must be placed on that key.
Find the minimum possible fatigue level at the end of the performance.

Constraints

$1\le N\le 100$
$1\le A_i\le 100$
$N$ and $A_i$ are integers.
$S_i$ is L or R.

Input

The input is given from Standard Input in the following format:

$N$
$A_1$ $S_1$
$A_2$ $S_2$
$⋮$
$A_N$ $S_N$

Output

Print the minimum fatigue level at the end of the performance.

Sample Input 1

4
3 L
6 R
9 L
1 R

Sample Output 1

11

For example, the performance can be done as follows:
Initially, place the left hand on key $3$ and the right hand on key $6$.
Press key $3$ with the left hand.
Press key $6$ with the right hand.
Move the left hand from key $3$ to key $9$. The fatigue level increases by $|9-3|=6$.
Move the right hand from key $6$ to key $1$. The fatigue level increases by $|1-6|=5$.
Press key $9$ with the left hand.
Press key $1$ with the right hand.
In this case, the fatigue level at the end of the performance is $6+5=11$, which is the minimum possible.

Sample Input 2

3
2 L
2 L
100 L

Sample Output 2

98

Sample Input 3

8
22 L
75 L
26 R
45 R
72 R
81 R
47 L
29 R

Sample Output 3

188

Solution

具体见文末视频。

Code

#include 
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int n;
	cin >> n;

	std::vector<int> a(n);
	std::vector<char> s(n);
	for (int i = 0; i < n; i ++)
		cin >> a[i] >> s[i];

	int res = 1e18;
	for (int i = 1; i <= 100; i ++)
		for (int j = 1; j <= 100; j ++) {
			int lo = i, ro = j, ans = 0;
			for (int k = 0; k < n; k ++) {
				if (s[k] == 'L') ans += abs(a[k] - lo), lo = a[k];
				else ans += abs(a[k] - ro), ro = a[k];
			}
			res = min(res, ans);
		}

	cout << res << endl;

	return 0;
}

C - Count Arithmetic Subarrays

Problem Statement

You are given a sequence of $N$ positive integers $A=(A_1,A_2,\dots ,A_N)$.
Find the number of pairs of integers $(l,r)$ satisfying $1\le l\le r\le N$ such that the subsequence $(A_l,A_{l+1},\dots ,A_r)$ forms an arithmetic progression.
A sequence $(x_1,x_2,\dots ,x_{|x|})$ is an arithmetic progression if and only if there exists a $d$ such that KaTeX parse error: Expected 'EOF', got '&' at position 25: …_i=d\ (1\leq i &̲lt; |x|).
In particular, a sequence of length $1$ is always an arithmetic progression.

Constraints

$1\le N\le 2\times 10^5$
$1\le A_i\le 10^9$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$
$A_1$ $A_2$ $\dots$ $A_N$

Output

Print the answer.

Sample Input 1

4
3 6 9 3

Sample Output 1

8

There are eight pairs of integers $(l,r)$ satisfying the condition: $(1,1),(2,2),(3,3),(4,4),(1,2),(2,3),(3,4),(1,3)$.
Indeed, when $(l,r)=(1,3)$, $(A_l,\dots ,A_r)=(3,6,9)$ is an arithmetic progression, so it satisfies the condition.
However, when $(l,r)=(2,4)$, $(A_l,\dots ,A_r)=(6,9,3)$ is not an arithmetic progression, so it does not satisfy the condition.

Sample Input 2

5
1 1 1 1 1

Sample Output 2

15

All pairs of integers $(l,r)(1\le l\le r\le 5)$ satisfy the condition.

Sample Input 3

8
87 42 64 86 72 58 44 30

Sample Output 3

22

Solution

具体见文末视频。

---

Code

#include 
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int n;
	cin >> n;

	std::vector<int> a(n);
	for (int i = 0; i < n; i ++)
		cin >> a[i];

	int len = 2, res = 0;
	for (int i = 2; i < n; i ++)
		if (a[i] - a[i - 1] == a[i - 1] - a[i - 2]) len ++;
		else res += (len - 1) * (len - 2) / 2, len = 2;
	res += (len - 1) * (len - 2) / 2;

	cout << res + n - 1 + n << endl;

	return 0;
}

D - Bonus EXP

Problem Statement

Takahashi will encounter $N$ monsters in order. The $i$-th monster $(1\le i\le N)$ has a strength of $A_i$.
For each monster, he can choose to either let it go or defeat it.

Each action awards him experience points as follows:
If he lets a monster go, he gains $0$ experience points.
If he defeats a monster with strength $X$, he gains $X$ experience points.

If it is an even-numbered defeated monster (2nd, 4th, …), he gains an additional $X$ experience points.
Find the maximum total experience points he can gain from the $N$ monsters.

Constraints

$1\le N\le 2\times 10^5$
$1\le A_i\le 10^9$
All input values are integers.

Input

The input is given from Standard Input in the following format:
$N$
$A_1$ $A_2$ $\dots$ $A_N$

Output

Print the maximum total experience points he can gain from the $N$ monsters as an integer.

Sample Input 1

5
1 5 3 2 7

Sample Output 1

28

If Takahashi defeats the 1st, 2nd, 3rd, and 5th monsters, and lets the 4th monster go, he gains experience points as follows:
Defeats a monster with strength $A_1=1$. He gains $1$ experience point.
Defeats a monster with strength $A_2=5$. He gains $5$ experience points. As it is the 2nd defeated monster, he gains an additional $5$ points.
Defeats a monster with strength $A_3=3$. He gains $3$ experience points.
Lets the 4th monster go. Takahashi gains no experience points.
Defeats a monster with strength $A_5=7$. He gains $7$ experience points. As it is the 4th defeated monster, he gains an additional $7$ points.
Therefore, in this case, he gains $1+(5+5)+3+0+(7+7)=28$ experience points.

Note that even if he encounters a monster, if he lets it go, it does not count as defeated.
He can gain at most $28$ experience points no matter how he acts, so print $28$.

As a side note, if he defeats all monsters in this case, he would gain $1+(5+5)+3+(2+2)+7=25$ experience points.

Sample Input 2

2
1000000000 1000000000

Sample Output 2

3000000000

Beware that the answer may not fit in a $32$-bit integer.

Solution

具体见文末视频。

---

Code

#include 
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int n;
	cin >> n;

	const int inf = 1e18;
	std::vector<int> a(n + 1);
	std::vector<vector<int>> dp(n + 1, vector<int>(2, -inf));
	for (int i = 1; i <= n; i ++)
		cin >> a[i];

	dp[0][0] = 0;
	for (int i = 1; i <= n; i ++)
		for (int j = 0; j < 2; j ++) {
			if (!j) dp[i][j] = max(dp[i - 1][j], dp[i - 1][j ^ 1] + a[i] * 2);
			else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j ^ 1] + a[i]);
		}

	cout << max(dp[n][0], dp[n][1]) << endl;

	return 0;
}

---

E - Sightseeing Tour

Problem Statement

There are $N$ islands and $M$ bidirectional bridges connecting two islands. The islands and bridges are numbered $1$, $2$, $\dots$, $N$ and $1$, $2$, $\dots$, $M$, respectively.

Bridge $i$ connects islands $U_i$ and $V_i$, and the time it takes to cross it in either direction is $T_i$.

No bridge connects an island to itself, but it is possible for two islands to be directly connected by more than one bridge.

One can travel between any two islands using some bridges.
You are given $Q$ queries, so answer each of them. The $i$-th query is as follows:

You are given $K_i$ distinct bridges: bridges $B_{i,1}, B_{i,2}, \ldots, B_{i,K_i}$.
Find the minimum time required to travel from island $1$ to island $N$ using each of these bridges at least once.
Only consider the time spent crossing bridges.
You can cross the given bridges in any order and in any direction.

## Constraints

$2\le N\le 400$
$N-1\le M\le 2\times 10^5$
KaTeX parse error: Expected 'EOF', got '&' at position 12: 1 \leq U_i &̲lt; V_i \leq N
$1\le T_i\le 10^9$
$1\le Q\le 3000$
$1\le K_i\le 5$
KaTeX parse error: Expected 'EOF', got '&' at position 16: 1 \leq B_{i,1} &̲lt; B_{i,2} <…
All input values are integers.
It is possible to travel between any two islands using some bridges.

Input

The input is given from Standard Input in the following format:

$N$ $M$
$U_1$ $V_1$ $T_1$
$U_2$ $V_2$ $T_2$
$⋮$
$U_M$ $V_M$ $T_M$
$Q$
$K_1$
$B_{1,1}$ $B_{1,2}$ $\cdots$ $B_{1,K_1}$
$K_2$
$B_{2,1}$ $B_{2,2}$ $\cdots$ $B_{2,K_2}$
$⋮$
$K_Q$
$B_{Q,1}$ $B_{Q,2}$ $\cdots$ $B_{Q,K_Q}$

Output

Print $Q$ lines. The $i$-th line ($1\le i\le Q$) should contain the answer to the $i$-th query as an integer.

Sample Input 1

3 5
1 2 10
1 3 20
1 3 30
2 3 15
2 3 25
2
1
1
2
3 5

Sample Output 1

25
70

For the first query, we need to find the minimum time to travel from island $1$ to island $3$ while using bridge $1$.
The minimum time is achieved by using bridge $1$ to move from island $1$ to island $2$, then using bridge $4$ to move from island $2$ to island $3$. The time taken is $10+15=25$.
Hence, print $25$ on the first line.
For the second query, we need to find the minimum time to travel from island $1$ to island $3$ while using both bridges $3$ and $5$.
The minimum time is achieved by using bridge $3$ to move from island $1$ to island $3$, then using bridge $5$ to move to island $2$, and finally using bridge $4$ to return to island $3$. The time taken is $30+25+15=70$.
Hence, print $70$ on the second line.

Sample Input 2

6 6
1 5 1
2 5 1
2 4 1
3 4 1
3 6 1
1 6 1
2
5
1 2 3 4 5
1
5

Sample Output 2

5
3

For each query, you can cross the specified bridges in either direction.

Sample Input 3

5 5
1 2 1000000000
2 3 1000000000
3 4 1000000000
4 5 1000000000
1 5 1000000000
1
1
3

Sample Output 3

4000000000

Beware that the answer may not fit in a $32$-bit integer.

Solution

具体见文末视频。

---

Code

#include 
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 4e2 + 10, M = 2e5 + 10;

int n, m, q;
int g[N][N], E[M][2], w[M];

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> n >> m;
	memset(g, 0x3f, sizeof g);
	for (int i = 1; i <= n; i ++) g[i][i] = 0;
	for (int i = 1; i <= m; i ++) {
		int a, b, c;
		cin >> a >> b >> c, E[i][0] = a, E[i][1] = b, w[i] = c;
		g[a][b] = g[b][a] = min(g[a][b], c);
	}

	for (int k = 1; k <= n; k ++)
		for (int i = 1; i <= n; i ++)
			for (int j = 1; j <= n; j ++)
				g[i][j] = min(g[i][k] + g[k][j], g[i][j]);

	cin >> q;
	while (q -- ) {
		int len;
		cin >> len;
		std::vector<int> b(len + 1);
		int more = 0;
		for (int i = 1; i <= len; i ++) cin >> b[i], more += w[b[i]];

		int res = 1e18;
		do {
			for (int i = 0; i < 1 << len; i ++) {
				int cost = 0;
				cost += g[1][E[b[1]][i & 1]] + g[E[b[len]][((i >> len - 1) & 1) ^ 1]][n];
				for (int j = 1; j < len; j ++)
					cost += g[E[b[j]][((i >> j - 1) & 1) ^ 1]][E[b[j + 1]][i >> j & 1]];
				res = min(res, cost);
			}
		}while (next_permutation(b.begin() + 1, b.end()));
		cout << res + more << endl;
	}

	return 0;
}

---

F - Gather Coins

Problem Statement

There is a grid with $H$ rows and $W$ columns.
Let $(i,j)$ denote the cell at the $i$-th row from the top and $j$-th column from the left.
There are $N$ coins on this grid, and the $i$-th coin can be picked up by passing through the cell $(R_i,C_i)$.
Your goal is to start from cell $(1,1)$, repeatedly move either down or right by one cell, and reach cell $(H,W)$ while picking up as many coins as possible.
Find the maximum number of coins you can pick up and one of the paths that achieves this maximum.

Constraints

$2\le H,W\le 2\times 10^5$
$1\le N\le \min (HW-2,2\times 10^5)$
$1\le R_i\le H$
$1\le C_i\le W$
$(R_i,C_i)\ne (1,1)$
$(R_i,C_i)\ne (H,W)$
$(R_i,C_i)$ are pairwise distinct.
All input values are integers.

Input

The input is given from Standard Input in the following format:

$H$ $W$ $N$
$R_1$ $C_1$
$R_2$ $C_2$
$\vdots$
$R_N$ $C_N$

Output

Print two lines.
The first line should contain the maximum number of coins you can pick up.
The second line should contain one of the paths that achieves this maximum as a string of length $H+W-2$.
The $i$-th character of this string should be D if the $i$-th move is downward, and R if it is rightward.
If there are multiple paths that maximize the number of coins picked up, you may print any of them.

Sample Input 1

3 4 4
3 3
2 1
2 3
1 4

Sample Output 1

3
DRRDR

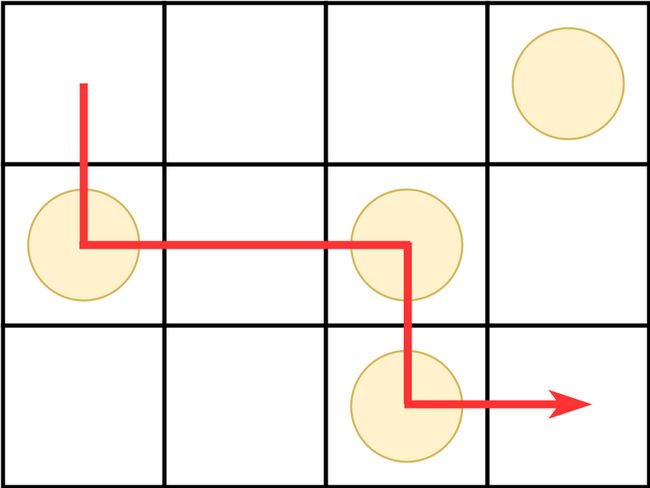
As shown in the figure above, by moving $(1,1)\to (2,1)\to (2,2)\to (2,3)\to (3,3)\to (3,4)$, you can pick up three coins at $(2,1),(2,3),(3,3)$.

Sample Input 2

2 2 2
2 1
1 2

Sample Output 2

1
DR

The path RD is also acceptable.

Sample Input 3

10 15 8
2 7
2 9
7 9
10 3
7 11
8 12
9 6
8 1

Sample Output 3

5
DRRRRRRRRDDDDDRRDRDDRRR

Solution

具体见文末视频。

---

Code

#include 
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int inf = 1e18;
struct info {
	int mx, idx;
	info(int _mx, int _idx): mx(_mx), idx(_idx) {}
};
info operator+ (info a, info b) {
	info c(-inf, 0);
	if (a.mx > b.mx) c.mx = a.mx, c.idx = a.idx;
	else c.mx = b.mx, c.idx = b.idx;
	return c;
}
struct fenwick {
	vector<info> tr;
	fenwick() {}
	fenwick(info x, int n) { init(x, n); }
	void init(info x, int n) { tr.resize(n + 1, x); }
	void add(int x, info d) {
		for (int i = x; i < tr.size(); i += (i & -i)) tr[i] = tr[i] + d;
	}
	info sum(int x) {
		if (!x) return info(-inf, 0);
		info res = info(-inf, 0);
		for (int i = x; i; i -= (i & -i)) res = res + tr[i];
		return res;
	}
};

const int N = 2e5 + 10;

int h, w, n;
PII pnt[N];
int dp[N], pre[N];

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> h >> w >> n;
	pnt[1] = {1, 1}, pnt[n + 2] = {h, w};
	for (int i = 2; i <= n + 1; i ++)
		cin >> pnt[i].fi >> pnt[i].se;
	sort(pnt + 1, pnt + 1 + n + 2);

	fenwick mx(info(-inf, 0), w);
	dp[1] = 0, mx.add(1, info(0, 1));
	for (int i = 2; i <= n + 2; i ++) {
		dp[i] = mx.sum(pnt[i].se).mx + (i != n + 2);
		pre[i] = mx.sum(pnt[i].se).idx, mx.add(pnt[i].se, info(dp[i], i));
	}

	cout << dp[n + 2] << endl;
	int lst = n + 2;
	std::vector<int> way;
	while (pre[lst])
		way.push_back(lst), lst = pre[lst];
	way.push_back(lst);
	reverse(way.begin(), way.end());
	for (int i = 1; i < way.size(); i ++) {
		for (int j = 1; j <= abs(pnt[way[i]].fi - pnt[way[i - 1]].fi); j ++)
			cout << 'D';
		for (int j = 1; j <= abs(pnt[way[i]].se - pnt[way[i - 1]].se); j ++)
			cout << 'R';
	}
	cout << endl;

	return 0;
}

---

G - As far as possible

Problem Statement

You are given a tree with $N$ vertices.
The vertices are numbered $1$, $2$, $\dots$, $N$.

The $i$-th edge ($1\le i\le N-1$) connects vertices $U_i$ and $V_i$, with a length of $L_i$.
For each $K=1,2,\dots ,N$, solve the following problem.

Takahashi and Aoki play a game. The game proceeds as follows. First, Aoki specifies $K$ distinct vertices on the tree. Then, Takahashi constructs a walk that starts and ends at vertex $1$, and passes through all the vertices specified by Aoki. The score is defined as the length of the walk constructed by Takahashi. Takahashi wants to minimize the score, while Aoki wants to maximize it. Find the score when both players play optimally.

Definition of a walk A walk on an undirected graph (possibly a tree) is a sequence of $k$ vertices and $k-1$ edges $v_1,e_1,v_2,\ldots,v_{k-1},e_{k-1},v_k$ (where $k$ is a positive integer) such that edge $e_i$ connects vertices $v_i$ and $v_{i+1}$. The same vertex or edge can appear multiple times in the sequence. A walk is said to pass through vertex $x$ if there exists at least one $i$ ($1\leq i\leq k$) such that $v_i=x$. (There can be multiple such $i$.) The walk is said to start and end at $v_1$ and $v_k$, respectively, and the length of the walk is the sum of the lengths of $e_1$, $e_2$, $\ldots$, $e_{k-1}$. ## Constraints

$2\le N\le 2\times 10^5$
KaTeX parse error: Expected 'EOF', got '&' at position 10: 1\leq U_i&̲lt;V_i\leq N
$1\le L_i\le 10^9$
All input values are integers.
The given graph is a tree.

Input

The input is given from Standard Input in the following format:

$N$
$U_1$ $V_1$ $L_1$
$U_2$ $V_2$ $L_2$
$⋮$
$U_{N-1}$ $V_{N-1}$ $L_{N-1}$

Output

Print $N$ lines.
The $i$-th line $(1\le i\le N)$ should contain the answer to the problem for $K=i$.

Sample Input 1

5
1 2 3
2 3 5
2 4 2
1 5 3

Sample Output 1

16
22
26
26
26

For $K=1$, Aoki’s optimal move is to specify vertex $3$, and Takahashi’s optimal move is to construct a path vertex $1$ $\to$ vertex $2$ $\to$ vertex $3$ $\to$ vertex $2$ $\to$ vertex $1$, resulting in a score of $16$.
For $K=2$, Aoki’s optimal move is to specify vertices $3$ and $5$, and Takahashi’s optimal move is to construct a path such as vertex $1$ $\to$ vertex $5$ $\to$ vertex $1$ $\to$ vertex $2$ $\to$ vertex $3$ $\to$ vertex $2$ $\to$ vertex $1$, resulting in a score of $22$.
For $K\ge 3$, the score when both players play optimally is $26$.

Sample Input 2

3
1 2 1000000000
2 3 1000000000

Sample Output 2

4000000000
4000000000
4000000000

Beware that the answer may not fit in a $32$-bit integer.

Solution

具体见文末视频。

---

Code

#include 
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 2e5 + 10, M = 4e5 + 10;

int n;
int h[N], e[M], ne[M], w[M], idx;
int dep[N], fa[N][20], d[N], pre[N], nxt[N], res[N], val[N], dis[N];
std::vector<int> leaf;

void add(int a, int b, int c) {
	e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs(int u, int par) {
	if (d[u] == 1) leaf.push_back(u);
	for (int i = 1; i < 20; i ++) fa[u][i] = fa[fa[u][i - 1]][i - 1];
	for (int i = h[u]; ~i; i = ne[i]) {
		int v = e[i];
		if (v == par) continue;
		dep[v] = dep[u] + 1, dis[v] = dis[u] + w[i], fa[v][0] = u;
		dfs(v, u);
	}
}
int lca(int u, int v) {
	if (dep[u] < dep[v]) swap(u, v);
	for (int i = 19; i >= 0; i --)
		if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];
	if (u == v) return u;
	for (int i = 19; i >= 0; i --)
		if (fa[u][i] != fa[v][i]) u = fa[u][i], v = fa[v][i];
	return fa[u][0];
}
int dist(int u, int v) {
	return dis[u] + dis[v] - 2 * dis[lca(u, v)];
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> n;
	memset(h, -1, sizeof h);
	for (int i = 1; i < n; i ++) {
		int u, v, l;
		cin >> u >> v >> l;
		add(u, v, l), add(v, u, l), d[u] ++, d[v] ++;
	}
	dfs(1, -1);

	pre[leaf[0]] = 1;
	for (int i = 1; i < leaf.size(); i ++)
		pre[leaf[i]] = leaf[i - 1], nxt[leaf[i - 1]] = leaf[i];
	nxt[leaf.back()] = 1;

	set<PII> S;
	for (auto v : leaf) {
		val[v] = -(dist(pre[v], nxt[v]) - dist(pre[v], v) - dist(v, nxt[v]));
		S.insert({val[v], v}), res[leaf.size()] += dist(pre[v], v);
	}
	res[leaf.size()] += dist(leaf.back(), 1);
	// for (auto v : S)
	// 	cout << v.fi << " " << v.se << endl;
	int tot = leaf.size();
	while (S.size()) {
		auto tmp = *S.begin();
		S.erase(S.begin()), tot --;

		res[tot] = res[tot + 1] - tmp.fi;
		nxt[pre[tmp.se]] = nxt[tmp.se];
		pre[nxt[tmp.se]] = pre[tmp.se];
		if (pre[tmp.se] != 1) {
			int v = pre[tmp.se];
			S.erase({val[v], v});
			val[v] = -(dist(pre[v], nxt[v]) - dist(pre[v], v) - dist(v, nxt[v]));
			S.insert({val[v], v});
		} if (nxt[tmp.se] != 1) {
			int v = nxt[tmp.se];
			S.erase({val[v], v});
			val[v] = -(dist(pre[v], nxt[v]) - dist(pre[v], v) - dist(v, nxt[v]));
			S.insert({val[v], v});
		}
	}

	for (int i = 1; i <= n; i ++) {
		if (i <= leaf.size()) cout << res[i] << endl;
		else cout << res[leaf.size()] << endl;
	}

	return 0;
}

---

视频题解

AtCoder Beginner Contest 369（A ~ G 题讲解）

---

最后祝大家早日