【初阶数据结构篇】栈的实现(附源码)
栈
- 1.概念与结构
- 2.栈的实现
-
- 2.1栈的初始化和销毁
- 2.2栈顶插入和删除数据
-
- 2.2.1栈顶插入数据(压栈)
- 2.2.2 栈顶删除数据(出栈)
- 2.3 取栈顶数据
- 2.4 获取栈的有效数据个数
- 2.5 打印栈中数据
1.概念与结构
栈:⼀种特殊的线性表,其只允许在固定的⼀端进⾏插⼊和删除元素操作。进⾏数据插⼊和删除操作的⼀端称为栈顶,另⼀端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。(先进来的后出去,先出去的后进来)
压栈:栈的插⼊操作叫做进栈/压栈/⼊栈,⼊数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
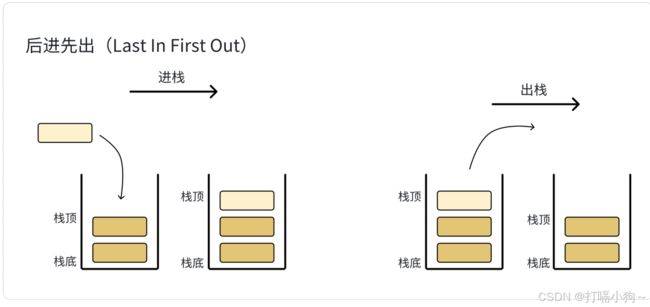
后来者居上
栈的实现⼀般可以使⽤数组或者链表实现,相对⽽⾔数组的结构实现更优⼀些。因为数组在尾上插⼊数据的代价⽐较⼩。
顺序表的底层是数组 逻辑结构都是线性的
队列的底层是链表 逻辑上连续,物理上不一定连续
2.栈的实现
stack.h
#pragma once
#include test.c
void STTest01()
{
ST st;
STInit(&st);
STPush(&st, 1);
STPush(&st, 2);
STPush(&st, 3);
STPush(&st, 4);
STPush(&st, 5);
/*STPop(&st);
STPop(&st);
STPop(&st);
STPop(&st);
STPop(&st);*/
printf("size: %d\n", STSize(&st));
while (!STEmpty(&st))
{
STDatatype data = STTop(&st);
printf("%d ", data);
STPop(&st);
}
printf("\n");
printf("size: %d\n", STSize(&st));
}
int main()
{
STTest01();
return 0;
}
stack.c
函数方法的实现
注意:在每一个方法的第一排都使用assert宏来判断ps是否为空(避免使用时传入空指针,后续解引用都会报错)
2.1栈的初始化和销毁
void STInit(ST* ps)
{
assert(ps);
ps->arr = NULL;
ps->capacity = ps->top = 0;
}
void STDestroy(ST* ps)
{
assert(ps);
if (ps->arr) //检查ps的arr成员是否非空
free(ps->arr); //如果非空,使用free函数释放这块内存
ps->arr = NULL; //将ps的arr成员设置为NULL,表示不再指向任何动态分配的内存
ps->top = ps->capacity = 0; //将栈顶位置和栈容量重置为0
}
注意:栈的特性决定了它无法被遍历和随机访问和插入数据,只能在栈顶操作!!!所以打印方法不能和顺序表一样遍历,在后面会讲到
2.2栈顶插入和删除数据
2.2.1栈顶插入数据(压栈)
判断空间,二倍增容
void STPush(ST* ps, STDatatype x)
{
assert(ps);
//空间是否足够
if (ps->top == ps->capacity)
{
int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
STDatatype* tmp = (STDatatype*)realloc(ps->arr, newcapacity * sizeof(STDatatype));
if (tmp == NULL)
{
perror("realloc fail!");
exit(1);
}
ps->arr = tmp;
ps->capacity = 2 * newcapacity;
}
ps->arr[ps->top++] = x;
}
2.2.2 栈顶删除数据(出栈)
先判空,再删除
//删除数据的时候先判断栈是否为空
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
//出栈 栈顶 入数据 出数据
void STPop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));
--(ps->top); //只让top--即可,不影响后来的插入,因为数据会覆盖
}
2.3 取栈顶数据
//取栈顶元素
STDatatype STTop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));
return ps->arr[ps->top - 1];
}
2.4 获取栈的有效数据个数
//获取栈中有效元素个数
int STSize(ST* ps)
{
return ps->top;
}
2.5 打印栈中数据
栈不能通过遍历来打印,所以只有通过循环取栈顶元素后再让其出栈的方式来依次打印,打印完了栈也为空了
while (!STEmpty(&ST))
{
STDatatype data = STPop(&ST);
printf("%d ", data);
STPop(&ST);
}
希望大家多多指正
stack.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"stack.h"
//初始和销毁栈
void STInit(ST* ps)
{
assert(ps);
ps->arr = NULL;
ps->capacity = ps->top = 0;
}
void STDestroy(ST* ps)
{
assert(ps);
if (ps->arr) //检查ps的arr成员是否非空
free(ps->arr); //如果非空,使用free函数释放这块内存
ps->arr = NULL; //将ps的arr成员设置为NULL,表示不再指向任何动态分配的内存
ps->top = ps->capacity = 0; //将栈顶位置和栈容量重置为0
}
//入栈
void STPush(ST* ps, STDatatype x)
{
assert(ps);
//空间是否足够
if (ps->top == ps->capacity)
{
int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
STDatatype* tmp = (STDatatype*)realloc(ps->arr, newcapacity * sizeof(STDatatype));
if (tmp == NULL)
{
perror("realloc fail!");
exit(1);
}
ps->arr = tmp;
ps->capacity = 2 * newcapacity;
}
ps->arr[ps->top++] = x;
}
//删除数据的时候先判断栈是否为空
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
//出栈 栈顶 入数据 出数据
void STPop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));
--(ps->top); //只让top--即可,不影响后来的插入,因为数据会覆盖
}
//取栈顶元素
STDatatype STTop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));
return ps->arr[ps->top - 1];
}
//获取栈中有效元素个数
int STSize(ST* ps)
{
return ps->top;
}
栈不能通过遍历来打印,所以只有通过循环取栈顶元素后再让其出栈的方式来依次打印,打印完了栈也为空了!
while (!STEmpty(&ST))
{
STDatatype data = STPop(&ST);
printf("%d ", data);
STPop(&ST);
}