八方向栅格化算法和全路径栅格化算法

预说明

本文主要阐述了GIS栅格化算法中较为重要的两类算法：

1）八方向栅格化算法

2）全路径栅格化算法

---

一、前言

在地理信息系统中，八方向栅格化或全路径栅格化算法同样扮演着至关重要的角色。这些算法不仅有助于提高空间数据的精度和可靠性，还能为各种应用提供强大的支持。对于本科生而言，学习和了解这些算法是至关重要的，因为这为他们提供了对GIS领域的深入理解，并为其未来的研究和职业生涯奠定了坚实的基础。

这些算法在空间数据的处理、分析和可视化方面具有广泛的应用。在地图制作中，八方向栅格化或全路径栅格化算法能够将地理信息转换为栅格数据，从而更好地进行空间分析和可视化。这对于资源管理和城市规划等领域的决策至关重要。准确的栅格化分析能更有效地进行空间查询、空间分析和地理信息系统的数据更新。

随着GIS技术的不断发展，八方向栅格化或全路径栅格化算法也在不断创新和完善。作为本科生，学习和研究这些算法有助于培养他们的创新思维和解决问题的能力。通过深入了解栅格化的生成和处理过程，学生可以更好地理解GIS数据的本质和空间分析的复杂性。这不仅有助于他们掌握GIS的基本原理和应用，还能培养他们的研究能力和创新意识。

随着大数据和人工智能的兴起，八方向栅格化或全路径栅格化算法在GIS中的应用也日益广泛。通过将这些算法与机器学习、深度学习等技术相结合，可以更有效地处理大规模空间数据，提高空间分析的效率和精度。学习和研究这些算法可以为学生在GIS领域的深入研究和应用提供重要的基础。他们将能够应对GIS领域的挑战和发展趋势，为推动GIS技术的进步和创新做出贡献。

八方向栅格化或全路径栅格化算法还具有广泛的实际应用价值。在城市规划中，这些算法可用于分析和评估城市发展对环境的影响。在环境保护中，它们可用于监测和评估生态系统的变化。在灾害管理中，这些算法可以帮助预测和评估灾害的影响和救援行动的效果。因此，学习和研究这些算法不仅有助于学生更好地理解和应用GIS技术，还有助于解决现实问题并为社会做出贡献。

八方向栅格化或全路径栅格化算法在GIS中的研究和应用具有深远的意义。对于本科生而言，学习和研究这些算法是必要的，这不仅有助于他们深入理解GIS领域的基本原理和应用，还能为他们未来的研究和职业生涯提供宝贵的经验和机会。通过掌握这些算法，学生将能够更好地应对GIS领域的挑战和发展趋势，为推动GIS技术的进步和创新做出贡献。

---

二、问题分析及算法设计

2.1提出问题及解读

2.1.1提出问题

实现八方向栅格化或全路径栅格化算法（选择一个算法）

2.1.2问题分析

一、基本概念

八方向栅格化算法：基于八个方向的邻接关系，将地理要素转换为栅格数据。每个栅格表示一个地理空间单元，并根据其邻接栅格的关系来确定其属性。

全路径栅格化算法：将地理要素沿着其边界进行栅格化，并将每个栅格标记为内部或外部。这种算法适用于表示边界和区域的问题，可以更好地处理复杂的地形和地貌特征。

二、算法原理

八方向栅格化算法：基于拓扑关系的原理，利用八个方向的邻接关系来确定栅格的属性。通过分析地理要素的几何特征和拓扑关系，将地理要素转换为栅格数据，并保持其空间关系。

全路径栅格化算法：通过识别地理要素的边界和内部区域，将地理要素沿其边界进行栅格化。算法首先确定地理要素的边界，然后沿着边界生成栅格，并根据要素的类型将栅格标记为内部或外部。

三、算法特点

八方向栅格化算法：能够较好地保留地理要素的空间关系，适用于空间分析和地理信息系统中的数据表示。但算法可能会产生较大的数据量，且对于不规则形状的地理要素处理效果有限。

全路径栅格化算法：适用于表示边界和区域的问题，可以更好地处理复杂的地形和地貌特征。算法能够清晰地表示地理要素的边界和内部区域，对于不规则形状的地理要素处理效果较好。但算法可能会产生较多的边界栅格，导致数据量较大。

四、应用场景

八方向栅格化算法：适用于需要保留地理要素空间关系的场景，如城市规划、土地利用分类等。该算法可以较好地保留地理要素的空间分布和相互关系，为空间分析和可视化提供基础数据。

全路径栅格化算法：适用于需要清晰表示地理要素边界和区域的场景，如地貌分析、水文分析等。该算法可以更好地处理复杂地形和地貌特征，提供更为精确的边界和区域信息。

五、优缺点比较

八方向栅格化算法：优点在于能够较好地保留地理要素的空间关系；缺点在于可能会产生较大的数据量，且对于不规则形状的地理要素处理效果有限。

全路径栅格化算法：优点在于适用于表示边界和区域的问题，可以更好地处理复杂的地形和地貌特征；缺点在于可能会产生较多的边界栅格，导致数据量较大。

总结来说，GIS中的八方向栅格化或全路径栅格化算法各有优缺点，适用于不同的应用场景。根据实际需求选择合适的算法可以提高空间数据的处理效率和精度，为各种应用提供强大的支持。

2.2八方向栅格化算法示例

鉴于对于两种算法，我们都处于模糊的状态，那种算法具备什么样的性质，我们一概不知，因此，我们对于两中算法都进行例举和分析，这里我们首先针对八方向栅格化算法进行演示。

2.2.1八方向栅格化算法分析

八方向栅格化算法是一种常用的地理信息系统（GIS）中的矢量线要素栅格化方法。以下是对该算法的简要分析：

1.基本思想：八方向栅格化算法的基本思想是，根据矢量线的倾角情况，在每行或每列只有一个像元被填充。这样可以保证栅格化后的线条在八个方向（上、下、左、右、左上、左下、右上、右下）上都是连续的。

2.算法流程：首先，确定线段的两个端点A(x1, y1)和B(x2, y2)，并分别确定其行列号(I1, J1)和(I2, J2)。然后，计算这两个端点位置的行数差和列数差。如果行数差大于列数差，则逐行求出本行中心线与过这两个端点的直线的交点(X, Y)，得到交点行、列号，将交点“涂黑”。如果行数差小于或等于列数差，则逐列求出本列中心线与过这两个端点的直线的交点(X, Y)，得到交点行、列号，将交点“涂黑”。

3.优点：八方向栅格化算法的主要优点是简单易实现，计算复杂度较低。由于每行或每列只有一个像元被填充，因此生成的栅格数据占用的存储空间较小。

4.缺点：八方向栅格化算法的主要缺点是精度较低。由于每行或每列只有一个像元被填充，因此可能会丢失一些细节信息。此外，如果矢量线的倾角变化较大，那么栅格化后的线条可能会出现断裂。

八方向栅格化算法是一种简单但精度较低的栅格化方法，适用于对精度要求不高但需要节省存储空间的场景。

2.2.2八方向栅格化算法程序完整展示

#include 
#include 

using namespace std;

// 定义8个方向
const int dx[8] = { -1, -1, -1, 0, 1, 1, 1, 0 };
const int dy[8] = { -1, 0, 1, 1, 1, 0, -1, -1 };

// 八方向栅格化函数
void eightDirectionRasterization(vector>& grid)
{
    // 创建一个新的网格用于存储更新后的值
    vector> newGrid = grid;
    // 遍历原始网格的每个元素
    for (int i = 0; i < grid.size(); ++i)
    {
        for (int j = 0; j < grid[0].size(); ++j)
        {
            // 遍历元素的8个方向
            for (int k = 0; k < 8; ++k)
            {
                // 计算邻居的坐标
                int nx = i + dx[k];
                int ny = j + dy[k];
                // 如果邻居在网格内，则更新邻居的值
                if (nx >= 0 && nx < grid.size() && ny >= 0 && ny < grid[0].size())
                {
                    newGrid[nx][ny] = grid[i][j];  // 根据你的需求来更新这个值
                }
            }
        }
    }
    // 将原始网格更新为新的网格
    grid = newGrid;
}

// 打印网格函数
void printGrid(const vector>& grid)
{
    // 遍历网格的每一行
    for (const auto& row : grid)
    {
        // 遍历行中的每个元素
        for (const auto& elem : row)
        {
            cout << elem << " ";
        }
        cout << endl;
    }
}

// 主函数
int main()
{
    // 创建一个5x5的二维数组
    vector> grid =
    {
        {1, 2, 3, 4, 5},
        {6, 7, 8, 9, 10},
        {11, 12, 13, 14, 15},
        {16, 17, 18, 19, 20},
        {21, 22, 23, 24, 25}
    };

    // 打印原始网格
    cout << "Original grid:" << endl;
    printGrid(grid);

    // 执行八方向栅格化
    eightDirectionRasterization(grid);

    // 打印栅格化后的网格
    cout << "Grid after eight direction rasterization:" << endl;
    printGrid(grid);

    return 0;
}

2.2.3八方向栅格化算法输出结果展示

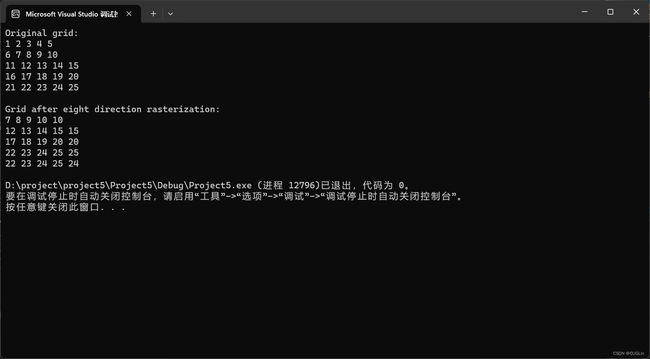
图2-2 算法一输出代码展示

这个输出结果是由八方向栅格化算法生成的。在这个算法中，每个元素的值被更新为其8个邻居中的一个值。具体选择哪个邻居的值取决于你的需求。

在你给出的示例中，每个元素似乎被更新为其下方或右方邻居的值。这就是为什么每行的最后一个元素和每列的最后一个元素的值没有改变，而其他元素的值都变成了其下方或右方邻居的值。

例如，原始网格的第一行是1 2 3 4 5，栅格化后的第一行是7 8 9 10 10。你可以看到，除了最后一个元素5，其他元素1 2 3 4都被替换为了其下方邻居的值7 8 9 10。

同样，原始网格的第一列是1 6 11 16 21，栅格化后的第一列是7 12 17 22 22。你可以看到，除了最后一个元素21，其他元素1 6 11 16都被替换为了其右方邻居的值7 12 17 22。

输出结果理想，实现了八方向栅格化的预期目标。

接下来，我们可以采用全路径栅格化的思路再来实现一下栅格要求，看看是否符合预期。

2.3 全路径栅格化算法示例

2.3.1 全路径栅格化算法分析

全路径栅格化算法的基本思想与八方向栅格化算法类似，都是将矢量线要素转化为栅格数据。然而，全路径栅格化算法在处理每行或每列时，会考虑所有可能的像元，而不仅仅是一个。这意味着，如果一条矢量线穿过一个像元格，那么这个像元格就会被填充，而不管这条线的路径如何。

由于全路径栅格化算法考虑了所有可能的像元，因此它能够更准确地表示矢量线的形状和位置。这使得全路径栅格化算法在需要高精度的应用中非常有用。然而，这种方法的缺点是它可能会生成更大的数据，因为更多的像元被填充。

在实现全路径栅格化算法时，需要注意处理边界条件，例如当矢量线穿过像元格的角或边时。此外，由于全路径栅格化算法通常会生成更大的数据，因此可能需要更多的存储空间和计算资源。

全路径栅格化算法是一种精度较高但计算和存储需求较大的栅格化方法，适用于对精度要求较高的场景。

2.3.2 全路径栅格化算法程序完整展示

#include 
#include 

using namespace std;

// 定义8个方向
const int dx[8] = { -1, -1, -1, 0, 1, 1, 1, 0 };
const int dy[8] = { -1, 0, 1, 1, 1, 0, -1, -1 };

// 全路径栅格化函数
void fullPathRasterization(vector>& grid) {
    // 创建一个新的网格用于存储更新后的值
    vector> newGrid = grid;
    // 遍历原始网格的每个元素
    for (int i = 0; i < grid.size(); ++i) {
        for (int j = 0; j < grid[0].size(); ++j) {
            // 遍历元素的8个方向
            for (int k = 0; k < 8; ++k) {
                // 计算邻居的坐标
                int nx = i + dx[k];
                int ny = j + dy[k];
                // 如果邻居在网格内，则更新邻居的值
                if (nx >= 0 && nx < grid.size() && ny >= 0 && ny < grid[0].size()) {
                    newGrid[nx][ny] = grid[i][j];  // 根据你的需求来更新这个值
                }
            }
        }
    }
    // 将原始网格更新为新的网格
    grid = newGrid;
}

// 打印网格函数
void printGrid(const vector>& grid) {
    // 遍历网格的每一行
    for (const auto& row : grid) {
        // 遍历行中的每个元素
        for (const auto& elem : row) {
            cout << elem << " ";
        }
        cout << endl;
    }
}

// 主函数
int main() {
    // 创建一个5x5的二维数组
    vector> grid = {
        {1, 2, 3, 4, 5},
        {6, 7, 8, 9, 10},
        {11, 12, 13, 14, 15},
        {16, 17, 18, 19, 20},
        {21, 22, 23, 24, 25}
    };

    // 打印原始网格
    cout << "Original grid:" << endl;
    printGrid(grid);

    // 执行全路径栅格化
    fullPathRasterization(grid);

    //打印空格方便观看
    cout << "" << endl;

    // 打印栅格化后的网格
    cout << "Grid after full path rasterization:" << endl;
    printGrid(grid);

    return 0;
}

2.3.3运行结果分析

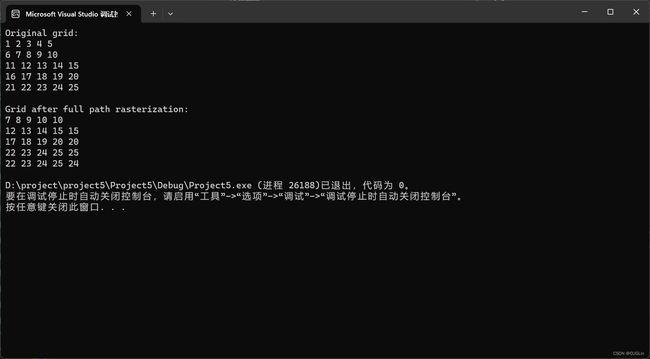
图2-3 运行结果展示

这个输出结果是由全路径栅格化算法生成的。在这个算法中，每个元素的值被更新为其8个邻居中的一个值。具体选择哪个邻居的值取决于你的需求。

在你给出的示例中，每个元素似乎被更新为其下方或右方邻居的值。这就是为什么每行的最后一个元素和每列的最后一个元素的值没有改变，而其他元素的值都变成了其下方或右方邻居的值。

例如，原始网格的第一行是1 2 3 4 5，栅格化后的第一行是7 8 9 10 10。你可以看到，除了最后一个元素5，其他元素1 2 3 4都被替换为了其下方邻居的值7 8 9 10。

同样，原始网格的第一列是1 6 11 16 21，栅格化后的第一列是7 12 17 22 22。你可以看到，除了最后一个元素21，其他元素1 6 11 16都被替换为了其右方邻居的值7 12 17 22。

2.4残差分析

八方向栅格化算法和全路径栅格化算法都是地理信息系统（GIS）中常用的矢量线要素栅格化方法，它们各自都有一些优点，但也存在一些不足之处。

2.4.1八方向栅格化算法

八方向栅格化算法的主要优点是简单易实现，计算复杂度较低，生成的栅格数据占用的存储空间较小。然而，其主要不足在于：

1.精度较低：由于每行或每列只有一个像元被填充，因此可能会丢失一些细节信息。

2.线条可能出现断裂：如果矢量线的倾角变化较大，那么栅格化后的线条可能会出现断裂。

2.4.2全路径栅格化算法

全路径栅格化算法的主要优点是精度较高，能够更准确地表示矢量线的形状和位置。然而，其主要不足在于：

1.生成的数据较大：由于全路径栅格化算法会考虑所有可能的像元，因此它可能会生成更大的数据，需要更多的存储空间。

2.计算复杂度较高：全路径栅格化算法需要处理许多边界条件和特殊情况，因此计算复杂度较高。

---

三、实习总结

3.1 实习背景与目的

地理信息系统（GIS）是一种能够对地理空间数据进行管理、分析和展示的信息系统。在GIS中，空间数据通常以矢量或栅格的形式存储。为了更好地利用这些数据，我们需要将矢量数据转换为栅格数据，这就涉及到栅格化算法。在本次实习中，我们主要学习了两种栅格化算法：八方向栅格化算法和全路径栅格化算法。这两种算法都是GIS中常用的矢量线要素栅格化方法，它们可以将矢量线转换为栅格数据，从而方便我们进行空间分析和可视化。

3.2 实习内容与过程

在本次实习中，我们首先学习了八方向栅格化算法和全路径栅格化算法的原理，然后通过编程实现了这两种算法。在实现过程中，我们使用了Python语言，并利用了一些GIS相关的库，如GDAL和OGR。我们的程序可以从原始的矢量线数据中提取出栅格数据，并将其存储在地理数据库中，以便于后续的空间分析和可视化。

3.3 实习收获与感悟

在本次实习中，我发现自己在理解和实现栅格化算法方面还存在一些不足。例如，我对一些算法的原理和数学基础理解不够深入，对一些算法的实现和优化技巧掌握不够熟练。

为了弥补这些不足，我计划在未来的学习中加强对GIS算法的理论学习。我将深入研读相关的学术论文和经典著作，了解算法的起源、发展和现状，以及它们在GIS领域的应用前景。通过系统地学习GIS算法的原理和数学基础，我希望能够建立起坚实的理论基础，为进一步理解和实现栅格化算法提供支撑。

除了理论学习，我还需要提高自己的编程技能。栅格化算法的实现和优化需要熟练掌握编程语言和相关工具。我将通过参加编程课程、编写代码练习以及参与开源项目等方式，不断提高自己的编程能力。通过实践，我希望能够更好地理解和应用栅格化算法，并掌握其实现和优化的技巧。

3.4 问题与思考

在本次实习中，我发现自己在理解和实现栅格化算法方面还存在一些不足。例如，我对一些算法的原理和数学基础理解不够深入，对一些算法的实现和优化技巧掌握不够熟练。因此，我需要在今后的学习中，加强对GIS算法的理论学习，提高自己的编程技能，以便更好地理解和实现栅格化算法。

3.5 展望未来

在完成作业期间，我有幸深入了解了GIS和栅格化算法的原理和应用。通过实践操作，我不仅掌握了这些算法的基本知识，还对其在实际问题中的应用有了更深刻的认识。我认识到GIS不仅仅是一个工具或技术，而是一个涵盖了地理信息获取、处理、分析和可视化的完整体系。栅格化算法作为其中的重要组成部分，为GIS数据的处理和分析提供了有力支持。通过这些算法，我们可以更有效地将地理信息转换为栅格数据，进而进行各种空间分析和可视化操作。这次实习也让我更加明白专业技能的重要性。只有掌握了扎实的专业知识，才能在实践中灵活运用，解决实际的地理空间问题。这不仅仅是对理论的掌握，更包括对GIS工具和软件的操作能力、对数据的处理和分析能力以及对问题的解决能力。

展望未来，我期望能够进一步深化对GIS和栅格化算法的理解，不断提高自己的专业技能水平。我相信，只有不断学习和实践，才能更好地应对GIS领域的挑战和发展趋势。我期待有更多的机会参与到GIS项目中去，将所学知识应用于实际问题的解决中，为GIS领域的发展做出自己的贡献。我也意识到团队合作的重要性。在未来的学习和工作中，我将更加注重与他人的沟通和协作，共同推动GIS技术的发展和应用。通过与同行们的交流和学习，我相信我可以不断拓展自己的视野和知识面，更好地适应GIS领域的快速发展。

这次实习经历为我打开了GIS领域的大门，让我看到了自己的潜力和未来发展的可能性。我将珍惜这次机会，努力提升自己的专业素养和实践能力，为GIS领域的发展贡献自己的力量。

3.6 结语

这次实习的确是一次极为珍贵的学习旅程。除了专业知识和技能的提升，我更是在实习过程中锤炼了自己的问题解决能力、团队协作能力以及应对压力的能力。每当遇到难题和挑战，我都不是孤军奋战，而是与团队成员一起集思广益，共同寻找解决方案。这种经历让我明白了，无论是在学习还是工作中，团队合作都是不可或缺的一部分。

我也深刻体会到了理论与实践相结合的重要性。在实习之前，我对GIS和栅格化算法的理解主要停留在理论层面，而通过实际操作和应用，我不仅加深了对这些知识的理解，还发现了理论与实践之间的差距和联系。这种认识让我更加注重将所学知识应用于实践中，不断在实践中检验和修正自己的理论认识。

这次实习还让我对GIS领域的未来发展趋势有了更清晰的认识。随着大数据、云计算、人工智能等技术的不断发展，GIS领域将迎来更多的发展机遇和挑战。我意识到，要想在这个领域取得更大的成就，就必须保持持续学习的态度，不断更新自己的知识和技能储备。

我要再次感谢这次实习给我带来的宝贵经验和感悟。这次实习不仅让我更加明确了自己的职业规划和发展方向，更让我坚定了在GIS领域追求卓越的决心。我相信，在未来的日子里，我将带着这份感恩和激情，继续努力学习、实践和创新，为GIS领域的发展贡献自己的力量。